前言

線性回歸中的線性係指 linear in parameters，也就是參數的線性，而非指解釋變數的線性或回歸線、反應平面（reponse surfaces）長得線性。本文將依解釋變數之個數，依序介紹簡單線性回歸、多元回歸與加廣型回歸模型。

簡單線性回歸 （Simple Linear Regression）

簡單線性回歸，其中的簡單指的是指有一個解釋變數 X ，其擬合一條直線，使個資料點到該線的距離最小。此處之距離係取 L2-norm 解釋模型，計算資料點到該線的垂直距離平方合使總距離合最小，模型為

且假設隨機誤差項滿足以下三假設

最小平方法

描述完模型與對隨機誤差項的假設後，還沒有說明如何找尋尚未知的參數 Beta0 與 Beta1。回歸模型的參數估計，對初學者而言，可能不知道什麼叫作參數、估計。在此可以簡單想成參數為在我們定義好一個模型大概長成什麼樣後，還有一些數值未知的變數，這些就叫作參數。而估計就是我們尋找（推理）未知參數的過程，把參數以數學方法表現出來。

對回歸模型主要有兩種方法估計參數：其一、為最小平方法（Least Square Estimation, LSE），其相應所需的模型假設已經如前面所述。其二、為最大概似估計法（Maximun Likelihood Estimation, MLE），其相應所需的模型假設就不只如前面所述，更假設模型的隨機誤差項為分配相同且獨立 （independent and identically distributed, iid）之常態分配。準確而言，若使用最大概似估計法估計參數，須假設

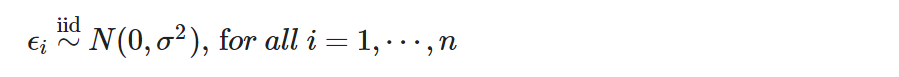
以利進行後續以「最大可能性」的概念做參數估計與統計推論。而以下本文沒有使用到這個假設。兩種假設的差別在於：在後者的假設下，可以對模型最更多的推論，但也在配飾模型後需檢視殘差項是否符合當初所訂的常態假設，在此就不細談，本文主要討論以最小平方法。

參數估計

回到簡單回歸模型，欲估計模型中的未知參數 B0 與 B1 ，以最小平方法（method of least square） 求取誤差平方合（sum of the squared error,　SSE） 的最小值，以其達到最小值時的參數值為該參數的估計量。也就是說，利用一組樣本代入模型計算後所得的預測點 ${\hat Yi = {\hat \beta_0} + {\hat \beta_1}X_i$ 與真實點 Yi 之間的差距平方合最小。找尋參數估計量，其中誤差平方合

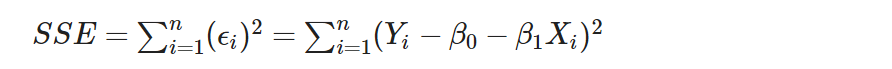
為求取誤差平方合的最小值，即

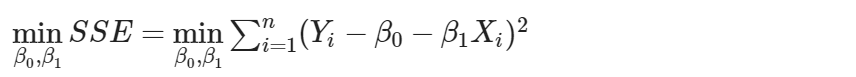
將 SSE 對未知參數 Beta0 與 Beta1 分別偏微分得並令其為零到

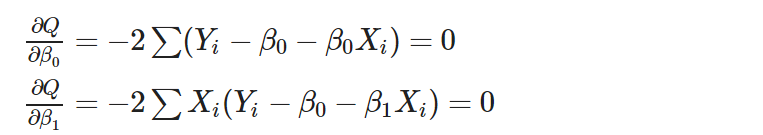
化簡後得到

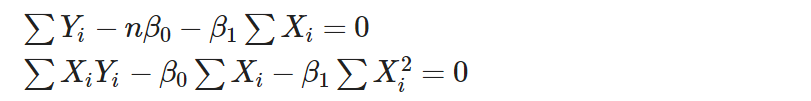
兩式取交集，移項推得

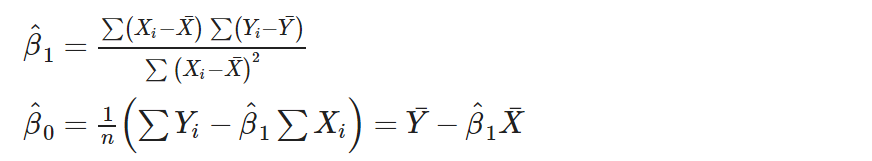
為簡單回歸模型最小平方法下的參數估計量。