在 HORS 裡，我們會將每個區塊所對應到的私鑰 sk_index 傳送給驗章者，驗章者再來檢查是否有

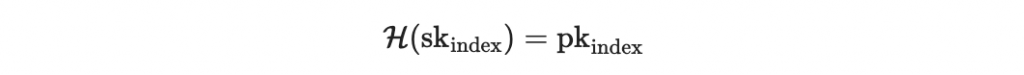
這樣的話，假設每個區段長度為 log2(t) 位元，那驗章者需要儲存 t 個公鑰。而其中 t 是二的某次方，並不小。這讓我們思考，是否可以使用 Merkle tree 的技術，讓驗章者只需儲存少量公鑰即可？

今天介紹兩個把 Merkle tree 跟 HORS 結合的簽章系統。

HORST 簽章系統

參數與鑰匙生成

參數

參數 t ：我們會把訊息分割為 log2(t) 的長度

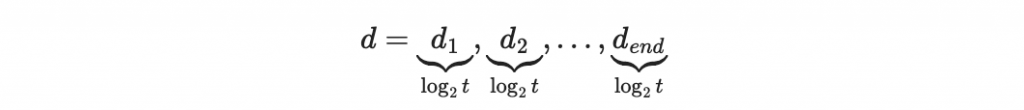
我們設定所使用的雜湊函數是使用 SHA-256 ，也設定這個訊息是雜湊函數後的結果（因此固定長度）

公私鑰

私鑰

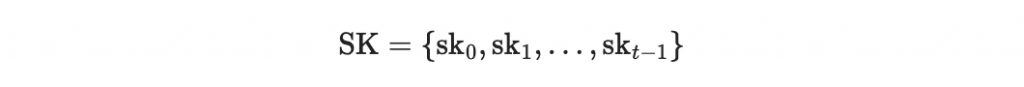
其中每個 sk 都是長度為 n = 256 的二進位字串。

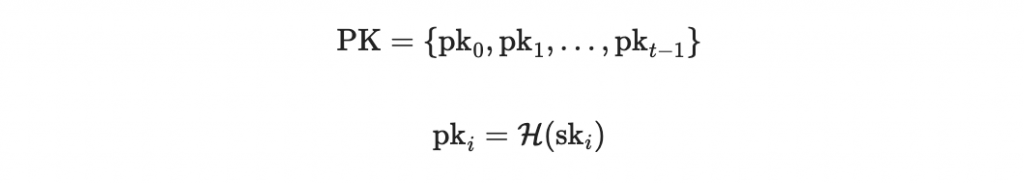
因為我們選用 SHA-256 所以每個 pk 都是 n = 256 長度的二進位字串。

此時，我們把這一堆公鑰 pk_0, ... pk_(t-1) 放入一個 Merkle tree 的最底層，並照 Merkle tree 的規則來算出 root 。將這個 root 發送為公鑰。

簽章

首先先進行訊息分段：

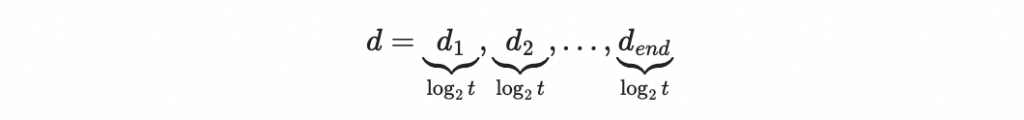
計算每個區塊的索引

並找出每段對應的私鑰 sk_index_i

除此之外，我們也提供從每個節點 pk_index_i 到 Merkle root 的必要材料 Auth_i 於是

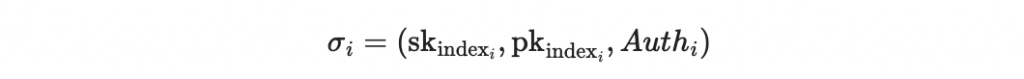
發送完整的簽名

驗章

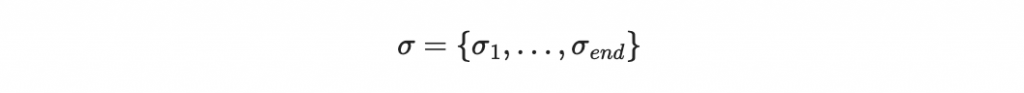
首先先進行訊息分段：

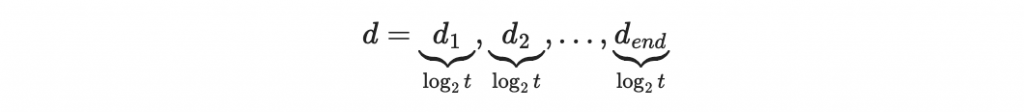
計算每個區塊的索引

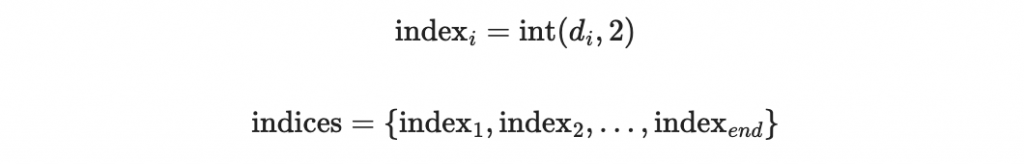
驗證所有索引的 hash 值

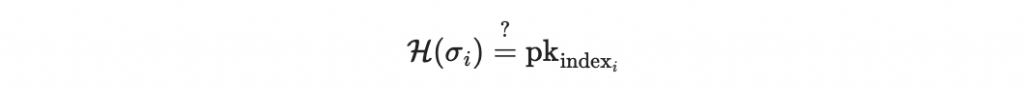
除此之外，我們也需驗證 pk_index_i 是否屬於總公鑰 pk 的 Merkle tree 裡。若兩個條件都達成，則此簽章為有效。

FORS 簽章系統

參數與鑰匙生成

參數

參數 t ：我們會把訊息分割為 log2(t) 的長度

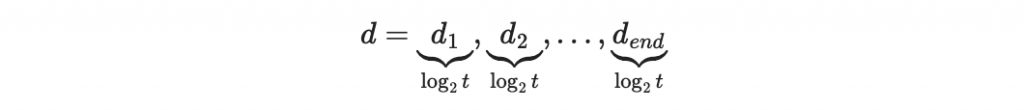
我們設定所使用的雜湊函數是使用 SHA-256 ，也設定這個訊息是雜湊函數後的結果（因此固定長度）。假設訊息被分段為 k 段。

公私鑰

我們會對每一個區塊都生成 w 個私鑰

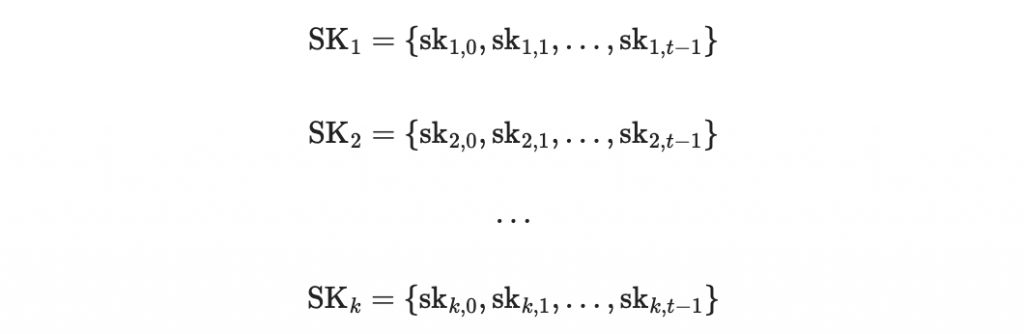
其中每個 sk_{i,j} 都是長度為 n = 256 的二進位字串。

對每一個 SK_i 都形成他的公鑰 PK_i

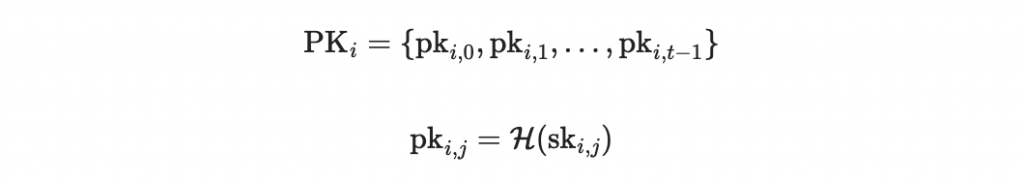
然後對每一組 PK_i 都形成他的 Merkle tree，於是一共會有 k 把Merkle root 總公鑰 mpk_1,...,mpk_k

簽章

首先先進行訊息分段：

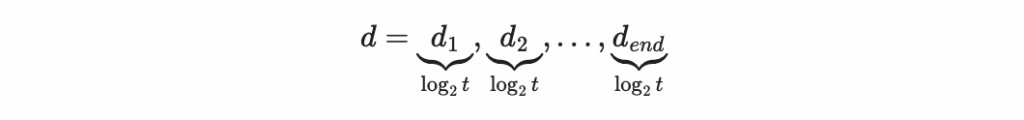
計算每個區塊的索引

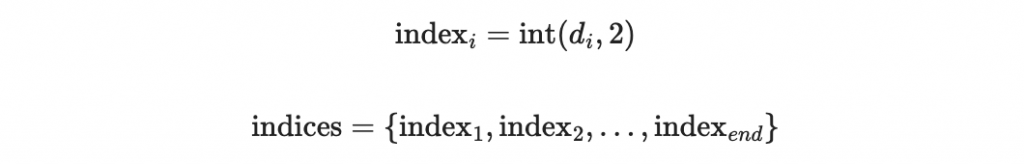
並找出每段對應的私鑰，第 d_i 段對應到

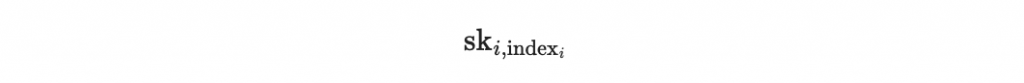
除此之外，我們也提供從每個節點 pk_index_i 到 Merkle root 的必要材料 Auth_i 於是

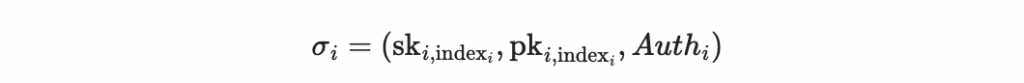
發送完整的簽名

驗章

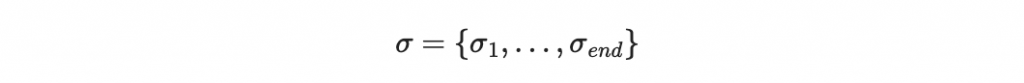
首先也先進行訊息分段：

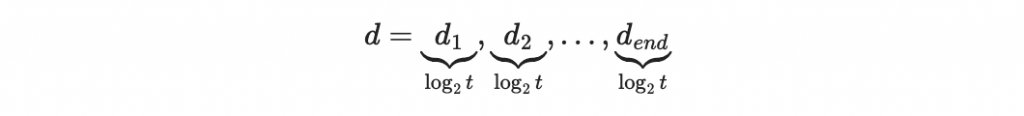
計算每個區塊的索引

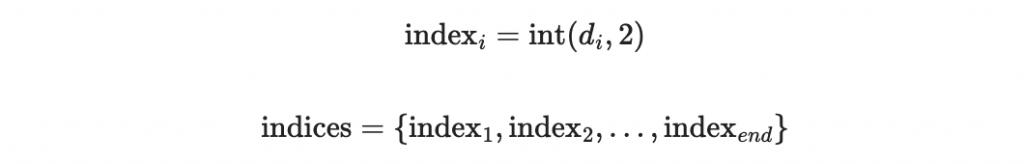
驗證所有索引的 hash 值

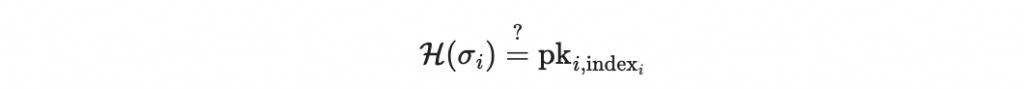
除此之外，我們也需驗證 pk_{i, index_i} 是否屬於總公鑰 mpk_i 的 Merkle tree 裡。若兩個條件都達成，則此簽章為有效。