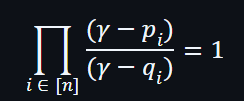基礎協議:連乘證明 (Grand Product Argument)

由於進行多項式編碼，所以會把多個單乘法壓縮成單次乘法的驗證。
這裡可以理解成將多個約束壓縮在一起，轉換成一個可驗證的多項式。
例子: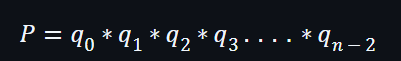

引入一個輔助向量 r: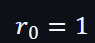

r是每一個對上計算的結果(Accumulator):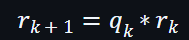

假設現在有3個約束，
第1個約束的起始值是1，而相關的公式是: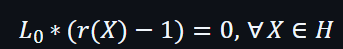

第2個約束(遞歸的乘法關系)的公式是: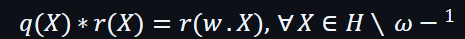

第3個約束:

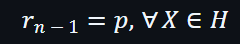
根據第3個約束，最後結果是: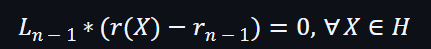

變成: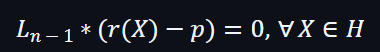

利用遞歸的乘法關系: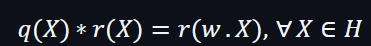

最後得出可以驗證的多項式:(以下是相關步驟)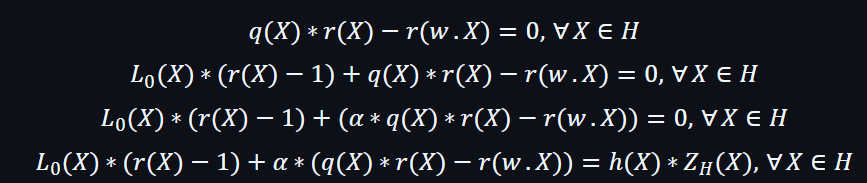

當中α是一個隨機數，h(X)是商多項式，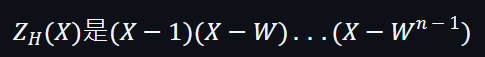

完成了以上證明又有什麼用呢?
其實會利用連乘證明來證明其他證明!

利用連乘證明來實現Multiset等價證明（Multiset Equality Argument）

假設向量 {qi} 為一個多項式 q(X) 的根集合，即對向量中的任何一個元素qi，都滿足q(ri)=0。這個多項式可以定義為：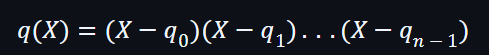

如果有另一多項式p(X)與q(x)相同，則會具有相同的根集合。
可以利用 Schwartz-Zippel 定理做檢驗，只要Verifier輸入一個隨機數 γ，Prover就可以通過下面的公式以證明向量 {pi} 和 {qi} 是在多重集合上是等價。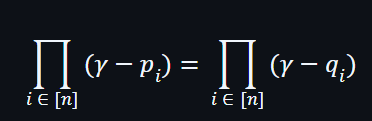

然後，再使用連乘證明完成驗證，通過加入輔助向量，轉換成可以驗證的多項式。在目前例子，兩個連乘公式可以轉換成為一個連乘公式: