由於每一輪都會涉及一定程度的計算，在這一篇就進一步簡化，希望可以讓大家在30天內能了解到什麼是PLONK，
同時也會在往後針對每一輪的計算作出深入解釋，這篇就算是為大家在深入理解之前打好一個底。
雖然今天是最後一篇，但不是終結，而是為了進階的學習打好基礎，在有足夠的基礎之下迎接新的學習。

第二輪

會利用複製限制來確保電路是線正確的及建立一個多項式的排列。
在進行運算之前，需要接收一個排列的挑戰，和第一輪得出的3個值，和一個進行配對的值。
然後綜合上述的3組輸入值再計算出一個排列多項式: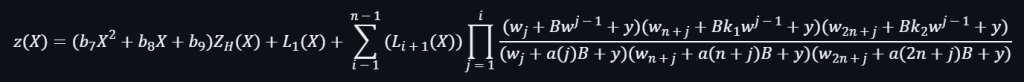

然後根據以上公式，可以計算出多項式的值: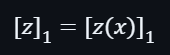

因此，在第二輪得出的輸出是: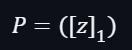

第三輪

利用排列多項式來確保複雜限制是滿足條件的，在過程中，證明者需要計算一個商挑戰，
同時也需要根據之前獲得到的資料(所以要記住在之前計算所得到的各種輸入和輸出)，來構建及計算一個商多項式t(X):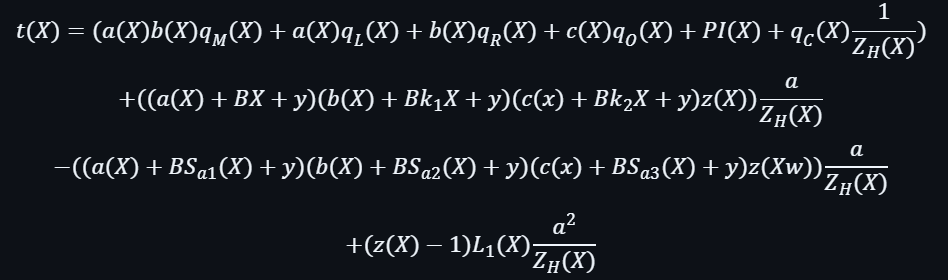

之後需要將t(x)拆分成為一個次方小於n的多項式: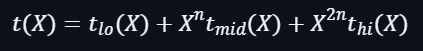

當中:

另外會有一些限制:

然後再進行計算: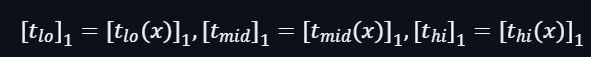

因此可以得出3部分的輸出: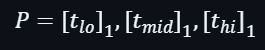

第四輪

證明者需要對於已提交的多項式中，計算橢圓曲線上指定的點的評估，
首先需要計算在指定點上打開的評估(針對證人的多項式上的點):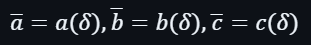

還有排列多項式及排列檢查多項式上的點的評估: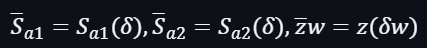

另外，需要計算一個在位置 δ 上的點的一個評估挑戰: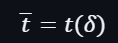

之後，需要計算另一個線性評估: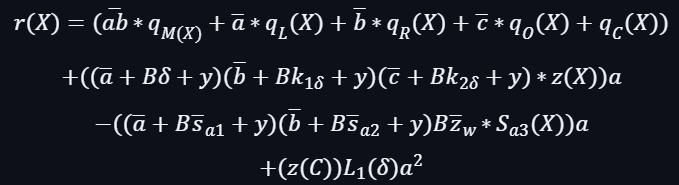

在建構多項式之後，會計算出: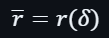

因為在第四輪的輸出是: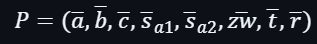

第五輪

需要計算多個多項式證明，而在計算前，需要先計算打開的挑戰 v 及計算線性多項式 r(X)。
然後綜合之前計算所得，可以進一步地去計算在以下點打開的多項式證明:


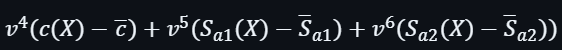
另外，還要計算在以下點打開的多項式證明: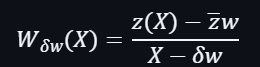

因此，根據上面所得到的兩個證明，進一步去計算: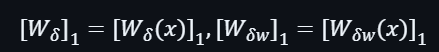

最後得出得輸出會是: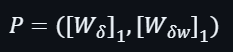

最後一步，就是綜合所有獲得的資料產出一個SNARK證明: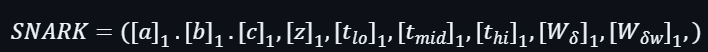

當成功產出SNARK證明後，可以用於進行不同點的評估挑戰，只要證明是真確，就可以成功進行驗證。