(Lattice) 格密碼學的基本定義
一個 n 維格 L 是 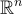 的任何子集,滿足以下兩點:
的任何子集,滿足以下兩點:
一個加法的子群: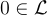
且對於每個 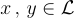 有
有 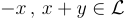
離散性:
每個 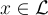 在
在 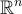
中有一個鄰域,其中 x 是唯一的格點。
例子:
包括整數格 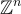 對於任何實數 c 和格
對於任何實數 c 和格 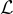 的縮放格
的縮放格 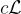 以及"棋盤"格
以及"棋盤"格 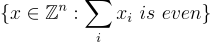
格 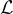 的最小距離是最短非零格向量的長度:
的最小距離是最短非零格向量的長度: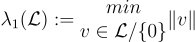 。
。
除非另有說明,||⋅|| 會表示歐幾里得範數。更一般地,第 i 個逐次最小值 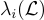 是最小的 r,使得
是最小的 r,使得 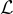 有 i 個線性獨立的範數不超過 r 的向量。 因為格
有 i 個線性獨立的範數不超過 r 的向量。 因為格 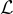 是
是 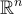 的加法子群,有商群
的加法子群,有商群 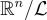 ,其陪集為
,其陪集為 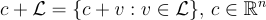 ,具有通常導出的加法運算
,具有通常導出的加法運算 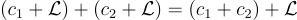 。
。 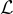 的一個基本域是集合
的一個基本域是集合 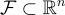 包含每個陪集
包含每個陪集 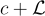 ,恰好一個代表
,恰好一個代表 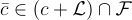 例如: 半開區間 [0,1) 和 [ −1/2 ,1/2 ) 是整數格
例如: 半開區間 [0,1) 和 [ −1/2 ,1/2 ) 是整數格 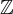 的基本域,其中陪集
的基本域,其中陪集 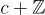 的代表分別是
的代表分別是 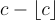 和
和 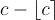 。
。
基與基本平行體
雖然每個非平凡的格 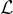 是無限的,但它總是作為某個線性獨立的基向量
是無限的,但它總是作為某個線性獨立的基向量 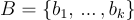 的整數線性組合有限生成:
的整數線性組合有限生成: 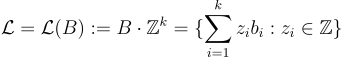
整數 k 稱為rank of the basic,是格的不變量。將注意力限制在 full-rank 格上,其中 k=n。格A 的基 B 不是唯一的:對於任何單位模的矩陣 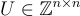 即行列式為 ±1 的矩陣,B⋅U 也是
即行列式為 ±1 的矩陣,B⋅U 也是 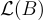 的基,因為
的基,因為 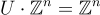 對於具有基 B 的格
對於具有基 B 的格 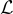 。
。
常用的基本域是以原點為中心的基本平行體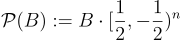
其中陪集 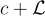 的代表是
的代表是 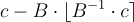 。
。
對偶格 (dual lattice)
格 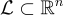 的對偶(有時稱為倒易)定義為
的對偶(有時稱為倒易)定義為 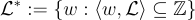 即與 L 中所有向量的內積 (inner products) 均為整數的點集。容易驗證
即與 L 中所有向量的內積 (inner products) 均為整數的點集。容易驗證 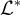 是一個格。
是一個格。
例如: 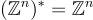 且對於任何非零實數 c 和格 L,有
且對於任何非零實數 c 和格 L,有 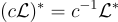 ,同樣容易驗證,如果 B 是 L 的基,則
,同樣容易驗證,如果 B 是 L 的基,則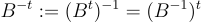 是
是 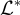 的基。
的基。
