密碼學進階構造 - MSIS

模-SIS (Module-SIS) 是短整數解問題從普通格推廣到模格上的一種變體。它旨在尋找一個由小係數多項式組成的非零向量，使得其與給定的多項式向量組的線性組合為零。

將 Ring-SIS 中的多項式

替換為中的多項式向量。

MSIS 對應的格結構比 Ring-SIS 的格結構簡單，
假設使用 MSIS 的模是 ，因此會有以下重點:

• 模  由 中長度為 k 的多項式向量組成。這些向量可以按分量進行加減，因此結果也是 中的一個向量。

• 中兩個向量的內積（乘法）會產生 中的一個多項式。

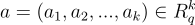• 的大小為 

MSIS(n, k, ℓ, q, B)
給定 （其中ℓ>k），找到 ，使得 ，
其中
且並非所有 都是 0。

注意：每個 ，現在是一個多項式向量：

因此，模-SIS 要求多項式矩陣方程有一個「小」的非零解：。

如果 是一個解，那麼 也是一個解。

MSIS(n, k, ℓ, q, B) 的等效表述
給定 ，找到非零的 （其中 m=ℓn），使得 Az=0(modq)，
其中

因此，MSIS 是 SIS 的一種特殊情況，其中矩陣 A 具有結構。

例子說明
假設 q=67, n=4, 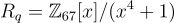，, k=2, ℓ=3, B=10。

因此 MSIS 實例：找到 ，不全為 0，滿足:

因此，會有
對 A 進行高斯消去法（模 q）得到以下簡化形式的矩陣：

所有滿足  的解 的集合是：

滿足  的解的總數是 

其中，非零且在 範圍內的解 r 的數量是 8。

MSIS 的解（最多可乘以 ±1, ±x, 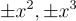）是：r=(6,−8,8,0,2,10,−6,3,−9,6,3,2)
多項式形式的解是：

檢查確認:
(i) 
(ii) 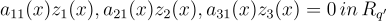中成立，且
(iii) 中成立。