在上一篇講解了屬性基加密的基礎，接下來再深入講解一下其用於用於任意電路的屬性基加密的情況。

26.1 適用於任意電路的屬性基加密
在先前基於雙線性對配的屬性基加密研究中，所支持的謂詞類別有一定限制，僅限於布爾公式。Gorbunov、Vaikuntanathan 和 Wee 的研究 [GVW13] 基於 LWE 構建了一種適用於任意謂詞的屬性基加密系統，這些謂詞可表示為任何先驗有界深度的電路，該深度在系統設定時固定。在此系統中，謂詞的私鑰大小與電路的規模成比例增長，大致對應於該謂詞的「混淆電路」，而密文及其屬性則提供了「混淆輸入」。
在 [GVW13] 之後不久，Boneh 等人 [BGG⁺14] 結合了 GSW 全同態加密（第 23.1 節）和適用於內積謂詞的屬性基加密的思想，構建了一種適用於任意先驗有界深度電路的屬性基加密系統。與 [GVW13] 相比，這裡的私鑰大小僅隨其謂詞的深度（而非規模）增長。以下我們描述 [BGG⁺14] 中構建的一個版本。

• 安裝設置與第25篇中的系統完全相同：主公鑰由一個（近乎）均勻隨機的矩陣 組成，該矩陣使用陷門生成；與 G 具有相同維度的均勻隨機矩陣 ，其中 ℓ 是屬性位元的數量；以及一個均勻隨機的症 主鑰是 的陷門。（我們在描述加密後討論謂詞的私鑰。）

• 加密基本上與第25篇中的屬性基加密相同，不同之處在於這裡我們僅使用二進制屬性/標籤。具體來說，要對屬性向量 加密消息位元
  ，輸出形式如下的密文：
  
  其中 是一個隨機 LWE 私鑰，近似值隱藏了適當的小誤差，且密文組件 以預期的方式對應於 。

• 對於謂詞 ，在不失一般性的情況下視為由 XOR（加法）和 AND（乘法）門組成的二進制電路，我們遞迴地定義一個矩陣 ，與第 23.1 節的全同態簽章方案完全相同：

1. 在基本情況中，當 （對於某個 i）時，令 。顯然，對於任何 ，我們有
   
   (26.1.2)

2. 若 （對於某些謂詞 ），則令 。觀察到對於任何 ，我們有
   
   (26.1.3)

3. 否則，若 （對於某些謂詞 ），則我們令 。觀察到對於任何 ，
   我們有
   
   (26.1.4)

為了使用 的陷門為謂詞 f 生成私鑰，我們對以下方程採樣一個高斯分佈的整數解 ：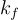

(26.1.5)

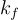• 若要使用某個謂詞 f（其中 f(x)=0）的私鑰 來解密具有已知屬性 的密文 ，我們首先對 這些組件進行操作，以計算
  
  計算方式如下所述。然後我們從下式中恢復訊息：
  
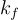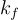  此近似成立是因為 是短的。（請注意，如果 f(x)≠0，則在 中出現的非零 G 倍數會阻止使用 進行解密。）為了獲得
  ，我們只需遞迴地應用方程式 (26.1.2)、(26.1.3) 和 (26.1.4)，來為參與計算 f 的每個子謂詞 g 獲得
  
  例如，如果g=g1⋅g2，則我們定義
  

請注意，由於我們在方程式 (26.1.3) 和 (26.1.4) 中乘上的矩陣是短的，因此近似值得以保持。另請注意，要應用方程式 (26.1.4)，我們需要知道  的值，這就是為什麼解密演算法需要知道屬性向量 x 的原因。

在適當的 LWE 假設下，上述方案在選擇性屬性攻擊下具有語義安全性，在這種攻擊中，敵手必須在看到主公鑰之前指定目標屬性向量 ，並且可以請求任何滿足 f(x∗)≠0 的謂詞 ff 的私鑰。安全性證明與之前幾篇的描述的證明非常相似，但在這裡，模擬器可以對標籤和隱藏的陷門進行任意（而不僅僅是線性）操作。更具體地說，矩陣 是從模擬器的輸入樣本構造的，並且模擬器將剩餘的主公鑰設置為 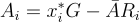，其中 是一些短矩陣。這種設置「穿刺」了主公鑰，使得對於任何合法的謂詞查詢 f（滿足 f(x∗)=1≠0），模擬器可以使用其 並透過方程式 (23.1.5) 和 (23.1.6) 計算出一個短的 ，使得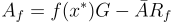
。因此，模擬器知道
 的一個短陷門，這允許它透過採樣方程式 (26.1.5) 的高斯解來回應查詢。此外，由於主公鑰在 處被穿刺，模擬器可以使用其輸入的
組件和 來生成一個挑戰密文，該密文要麼是正確分佈的，要麼在統計上隱藏訊息，這取決於挑戰是 LWE 分佈的還是均勻分佈的。

謂詞加密
我們在本章最後提一下，Gorbunov、Vaikuntanathan 和 Wee 的最新工作 [GVW15a] 基於 LWE 假設構建了謂詞加密。簡而言之，謂詞加密是屬性基加密的加強，在這種加密中，與密文相關聯的屬性對於未被授權解密該密文的（任何聯盟）用戶是隱藏的。
在 Gorbunov 等人的建構中，加密演算法使用 FHE 來加密屬性向量 x（在加密者選擇的新金鑰下），而解密演算法則對加密的 x 執行謂詞 f 的同態評估。當然，結果值 f(x)∈{0,1}仍然是加密的，但訊息的恢復應以這個位元為條件。這個問題透過以下方式解決：回想一下，FHE 解密是一個相對輕量的過程，包括密文與私鑰的取模 q 內積取整。同樣回想一下，我們有適用於內積謂詞的屬性隱藏 ABE 方案。因此，我們增強 PE 加密演算法，將 FHE 私鑰座標也作為隱藏屬性包含進來，並相應地擴展 PE 解密演算法，以計算私鑰與加密 f(x) 的最終 FHE 密文之間的內積。最後，透過將內積在 中對應於零加密的大約 q/2 個值中的每一個進行位移來完成取整。請注意，為了做到這一點，解密者需要每個位移有一個單獨的私鑰，並且在解密成功時會得知內積的確切值；這就是為什麼 PE 方案對未授權用戶隱藏屬性，但對授權用戶則不隱藏的原因。

參考資料
[GVW13] S. Gorbunov, V. Vaikuntanathan, and H. Wee. Attribute-based encryption for circuits. In STOC, pages 545–554. 2013.

[BGG+14] D. Boneh, C. Gentry, S. Gorbunov, S. Halevi, V. Nikolaenko, G. Segev, V. Vaikuntanathan, and D. Vinayagamurthy. Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In EUROCRYPT, pages 533–556. 2014.