題目介紹(64. Minimum Path Sum)：
這題屬於 動態規劃 (Dynamic Programming, DP) 的經典題型，主要考驗我們如何在一個二維網格 (grid) 中，找到從左上角走到右下角的最小路徑總和。
題目給定一個 m x n 的網格，每個格子都包含一個非負整數，代表進入該格子的代價。我們只能選擇 向右 (right) 或 向下 (down) 移動，無法往左或往上。要求是設計一個演算法，計算從 (0,0) 出發到 (m-1,n-1) 的最小路徑和。
成功執行畫面截圖: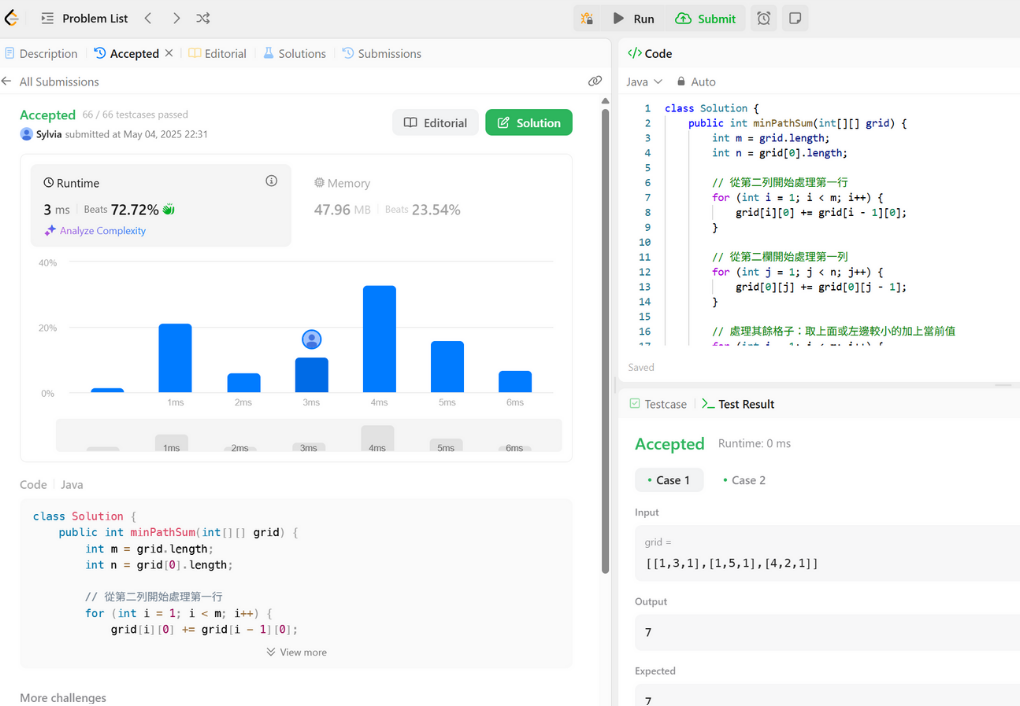

顯示前面其路徑截圖: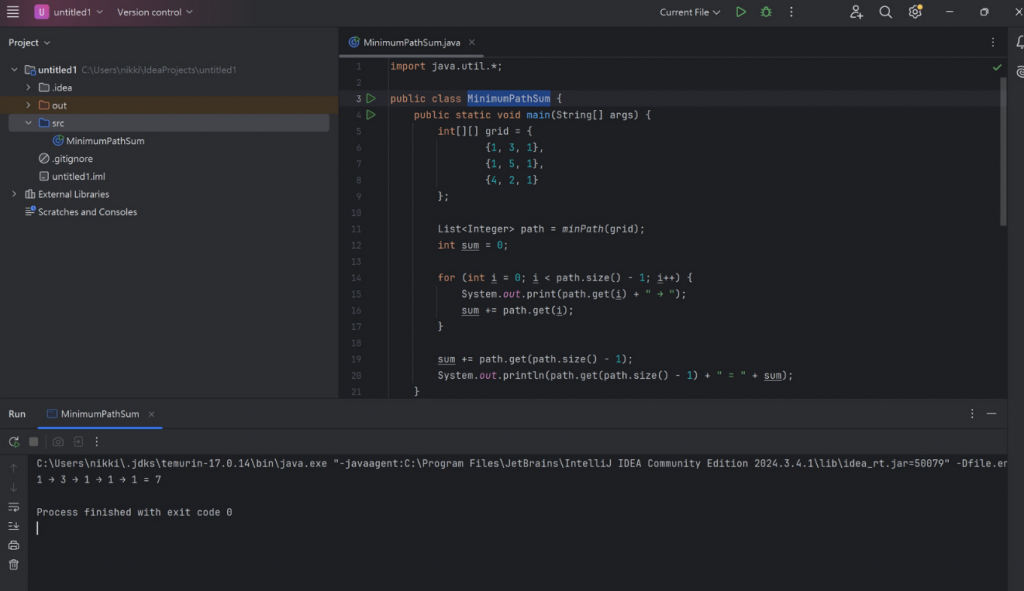

(用JAVA另寫程式碼，跑出結果讓我們更加了解路徑)
學習心得:
剛開始讀題時，我直覺想到用 DFS 或回溯去嘗試所有可能路徑，但很快發現這樣的時間複雜度太高，對於稍大一點的網格就會超時。這讓我意識到，單靠暴力解法並不能真正有效率地解決問題。轉換思路之後，我開始嘗試建立 DP 陣列，去記錄每個格子的最小路徑和。解完之後，我也嘗試用空間壓縮的方式，只保留一維陣列來存結果，發現程式更加簡潔。這次的練習讓我不僅強化了 DP 的理解，也學會在面對問題時，先思考能否找到規律與狀態轉移。
延伸邏輯結合時事面:
這題的核心在於：
1.只能往右或往下 → 代表現實中很多抉擇具有方向性與限制，我們無法「回頭重來」。
2.最小路徑和 → 就像我們在社會資源有限的情況下，如何找到「成本最低、效率最高」的方案。
3.動態規劃 → 每一步的最佳選擇，必須依賴「過去累積的最小代價」，而不是單看當下。

把這邏輯放到現在社會，可以延伸到：
1.醫療資源分配：醫院在安排 ICU 病床或急診資源時，往往要在有限的人力物力下，找到讓病人最有效益的照護方式，這跟「最小化代價」的思維相似。
2.都市交通規劃：捷運、公車或道路設計，都需要考慮「如何讓市民通勤的時間成本最小化」，而非單純建越多越好。
3.環境與能源議題：在能源轉型或碳排放減量的政策制定上，也必須找到「最少代價的路徑」，例如逐步減煤、增綠能的過程，就是動態規劃式的累積最優解。