前言

在開始學習之前，我們需要先理解一個最基本的概念，再複雜的模型，本質上都可以用 WX + b 來表示。這個公式是人工智慧中最基礎的基礎，但往往在任何一門 AI 課程裡，老師都不會直接告訴你這件事。今天我要分享的，就是這個公式究竟如何推理，並一步步導出正確答案。

單層感知器的數學公式

單層感知器（Perceptron）是深度學習中最基礎、也是最早提出的模型之一。它能夠模擬邏輯閘（如 AND 與 OR）的運算。其數學形式可表示為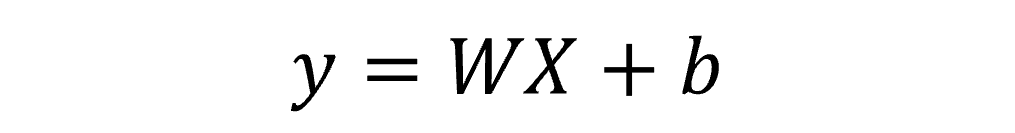

其中 𝑊 表示權重（weights）、 𝑋 表示輸入向量（inputs）、𝑏為偏置（bias），而在模型初始化時，權重通常會隨機設定，至於偏置有時可以省略，因為它主要用於調整資料的偏向性，我們可以先看到以下兩張圖片。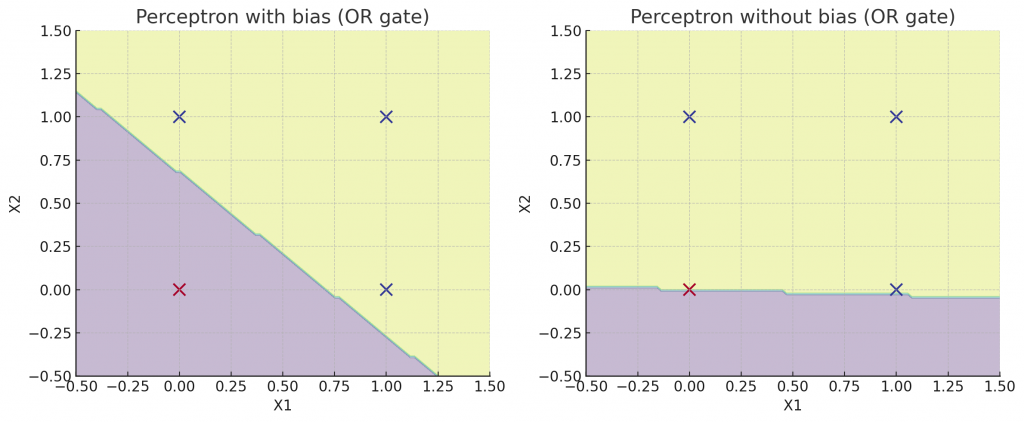

在左圖中由於引入了偏置，決策邊界得以適當平移，因此能正確區分 OR 邏輯閘的輸入資料。相較之下右圖中的決策邊界被迫通過原點 (0,0)，使得模型無法正確表示 OR 邏輯，因而產生分類錯誤。因此我們可以知道偏置的核心作用在於賦予模型調整決策邊界位置的彈性，避免受限於原點，從而更準確地刻劃資料的分布特性，不過讓我們回到剛剛的公式

在公式中可以看到，權重會直接與輸入相乘，因此它對模型輸出的影響遠大於偏置。這也代表著即便偏置的初始設定不理想，模型依然能透過不斷訓練來調整權重，最終收斂到正確的答案。

但對於模仿邏輯閘的動作，我們通過這樣的計算公式緊緊為很接近於1或0而已，實際上我們並沒有辦法完美貼近於1，因此在單層感知器上通常會使用階躍函數（Step Function）這一個激勵函數（Activation Function）來進行轉換，我們可以看到以下的數學式子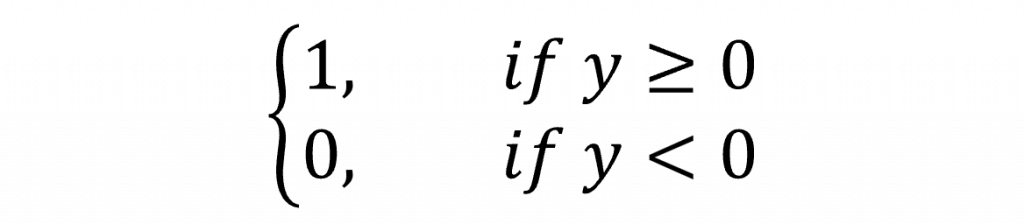

如此一來，我們便能完整地得到模型的輸出。而上述的計算流程，正是我們所稱的前向傳播（Forward Propagation），這個過程的核心在於將輸入數據傳遞並轉換為輸出結果，進而計算出模型的預測值。以上就是我們在學習深度學習的第一步，理解模型的構造並理解該模型的前向傳播中個參數的含意。

下集預告

今天我們理解了「權重」的重要性。不過你可能還不清楚該如何去最佳化這個參數。而這正是我們明天要學習的新數學方法的核心，只需要運用國中階段的知識，就能掌握。

但在進入新內容之前，我們不妨先思考一個問題：如何找到一個參數的變動速度與方向？這個問題的答案，將會是我們理解最佳化的關鍵起點。