前言

在學習深度學習模型的時候，很多同學常常會有一個疑問，模型是怎麼一步一步變得「更聰明」的呢？其實模型的進步並不是一次到位，而是透過不斷修正與調整來完成的。就好比學生做題目一樣，先嘗試寫答案，再根據老師批改的錯誤慢慢修正，最後才會越來越接近正確答案。

今天我們要談的，就是這個「修正錯誤」的過程，也就是所謂的模型最佳化。它的核心原理在於計算目標值（正確答案）與預測值（模型的答案）之間的誤差，然後利用這些誤差去更新模型的權重。透過這樣的循環，模型會一步一步學會如何更準確地做出預測，這個步驟也是整個深度學習訓練中最關鍵的一環。

模型如何計算誤差

昨天我們學習了模型的前向傳播，了解了模型是如何計算出答案的。但僅僅有答案還不夠，我們還需要知道「模型答得好不好」。這時候就需要引入損失函數（Loss Function）。

損失函數的作用，是透過比較模型的預測值（Prediction）與真實的目標值（Target），計算出它們之間的差距，這個差距就稱為損失（Loss）。損失越小，代表模型的預測越接近正確答案；反之損失越大，就表示模型還有很多地方需要改進，而其中我們最基本的損失函數就是均方誤差(Mean square error，MSE)，其數學公式為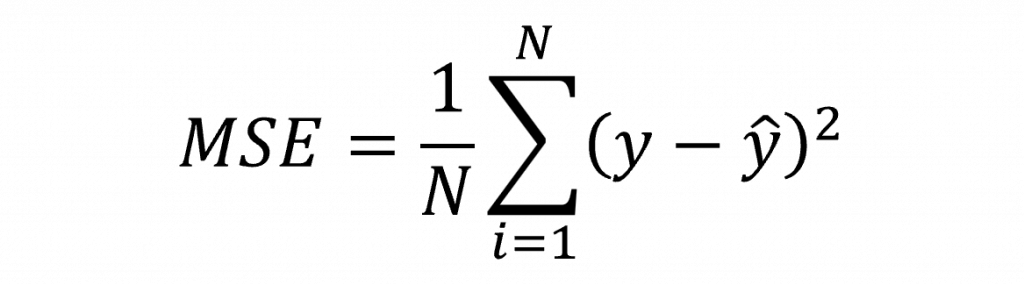

這種「利用目標值來指導模型學習」的方式，就是監督式學習（Supervised Learning）。你可以把它想像成一個老師在批改作業：模型寫出答案後，老師（損失函數）會根據正確答案指出錯誤的地方（損失），再幫助模型一步一步修正，直到能更精準地回答問題。

單層感知器的反向傳播

在單層感知器中我們的模型輸出可以表示為WX+b，其中，權重 𝑊 是需要透過訓練不斷更新與優化的核心參數。
優化的依據就是損失函數，也就是模型預測與真實標籤之間的差距。因此訓練的目標就是讓權重找到能夠使損失函數最小化的位置。我們可以將損失函數隨權重變化的關係繪製成如下圖所示的曲線：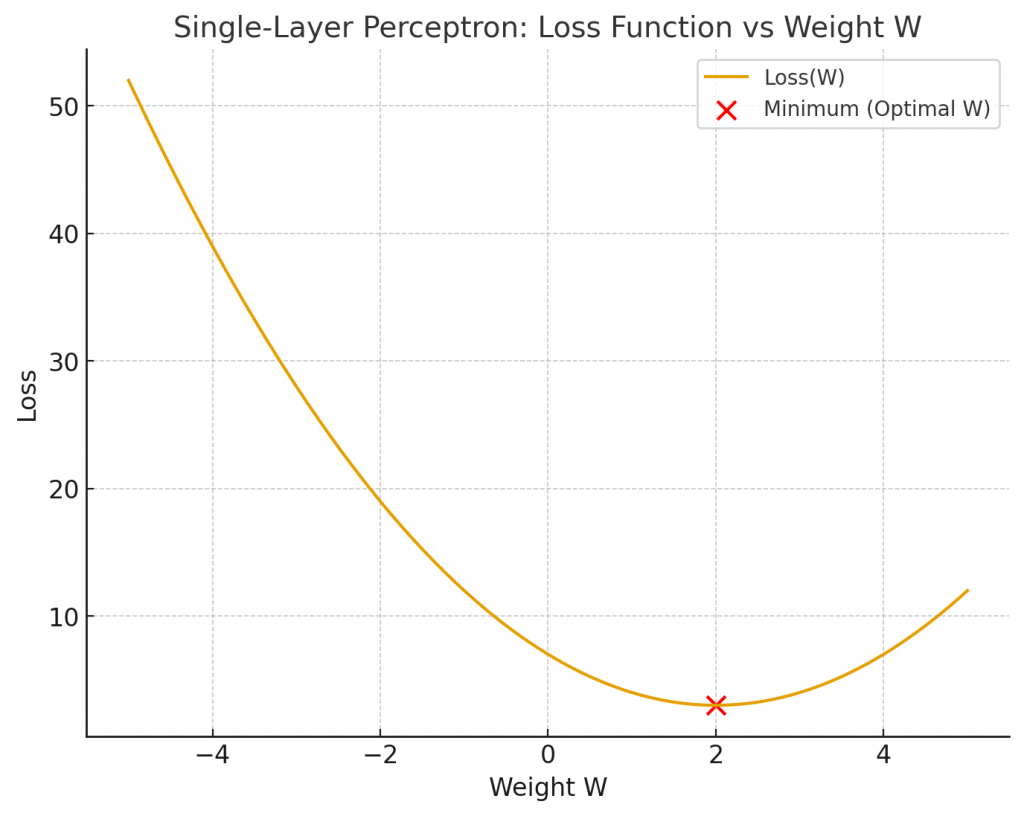

從圖中可以看到，損失函數會隨著權重 𝑊 的不同而變化，而我們的目標就是找到曲線的最低點。那麼如何讓權重一步步移動到這個最低點呢？

答案是我們需要知道當前權重的運動方向與速度，這可以透過損失函數對權重的偏導數來獲得，也就是計算出權重的梯度（Gradient）其中方向由梯度的正負號決定，指引權重該往左還是往右移動。速度則由梯度的絕對值大小決定，代表當前坡度的陡峭程度。

因此在反向傳播的第一步就是計算出∂L/∂W，但因損失函數為複合函數，因此我們先要使用連鎖率展開其算式，因此我們可以整理出以下公式：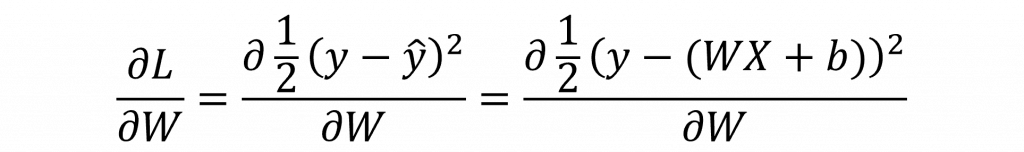

其中∂L/∂y^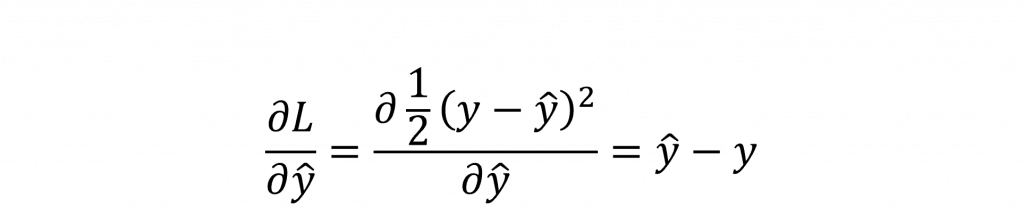

而∂y^/∂W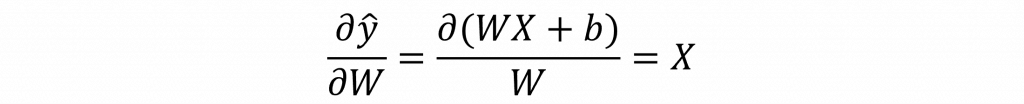

因此我們可得單層感知器的梯度公式為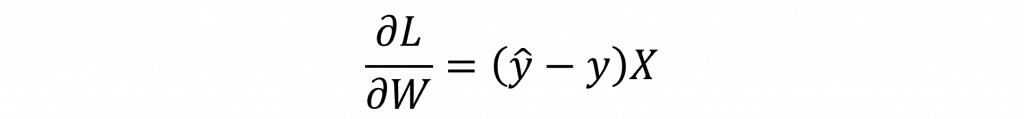

在推導出梯度公式後，我們便能利用梯度的大小來調整權重的 更新方向 與 更新速度。
但需要特別注意的是，如果更新步伐過大，雖然移動速度很快，卻可能因為跨越谷底而錯失最佳解，甚至在損失函數曲線上不斷震盪、無法收斂。

為了避免這種情況，我們引入一個稱為學習率 (learning rate)的超參數，用來控制每次更新的幅度。
基於此，梯度下降法 (Gradient Descent)的更新公式為：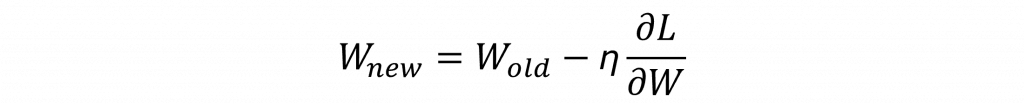

η：學習率，控制更新步伐大小

因此選擇合適的學習率是梯度下降能否順利找到最佳權重的關鍵。至此我們已完整說明了反向傳播的流程與數學推導。在深度學習的訓練過程中，模型透過不斷重複的前向傳播與反向傳播，不斷更新權重，最終找到最佳解。如此一來，模型便能根據不同的輸入資料，產生正確且對應的輸出結果。

下集預告

學習的關鍵在於「眼到、口到、心到、手到」。目前我們仍缺乏「手到」這一步的實踐，因此明天將示範如何使用 NumPy 來模擬各種邏輯閘，並觀察不同學習率與偏置對結果所帶來的影響。這一環節對於後續模型的優化具有至關重要的意義。