前言

昨天我們只用了一個 Wx + b 就能模擬出邏輯閘的運作情況。那麼，如果將多個 Wx + b 組合起來呢？這樣是否能處理更複雜的任務？答案是肯定的。第一個採用這種思路的方法，就被稱為多層感知器（MLP, Multi-Layer Perceptron）。

多層感知器的前向傳播

1.輸入層->隱藏層

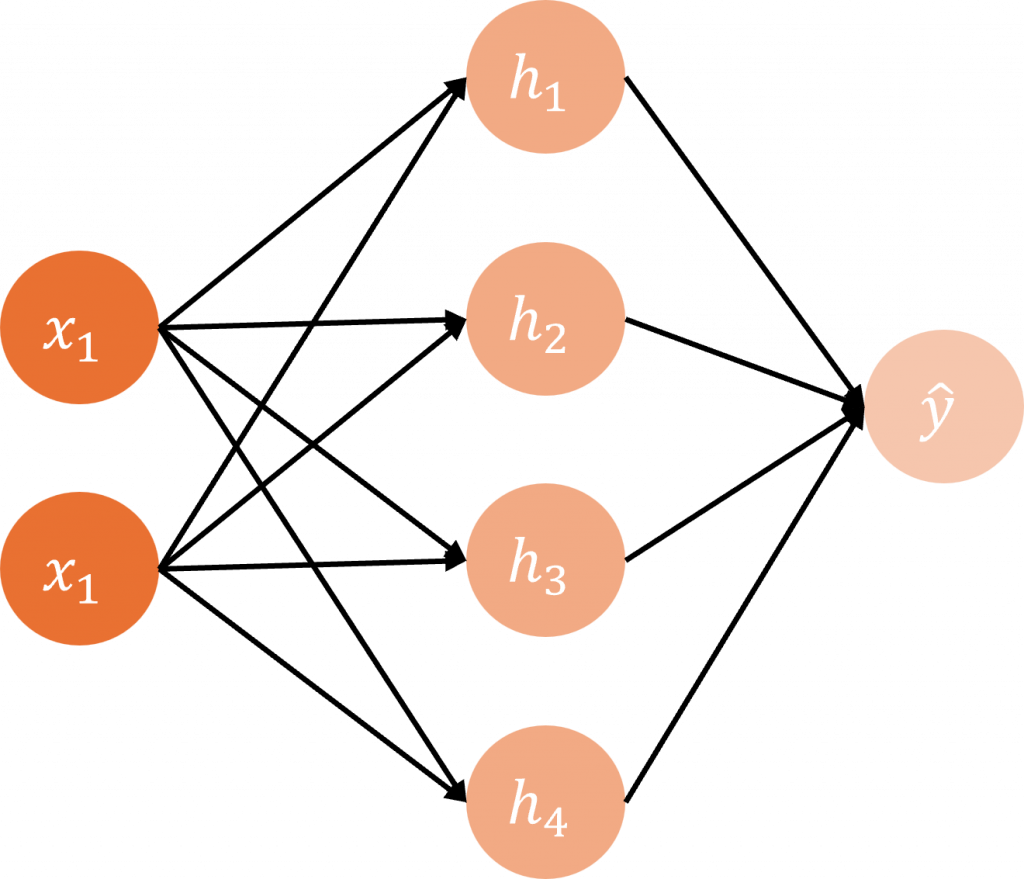
與單層感知器相比，多層感知器中的每一個隱藏層，都可以看作是由多個單層感知器的輸出所組成，就像圖片中的 h1 ~ h4 這些節點，其實就是單層感知器的輸出，而在多層感知器裡，這些組合起來的層被稱為隱藏層。在隱藏層中，我們同樣可以選擇不同的激勵函數，其中最常見的就是 ReLU（Rectified Linear Unit）。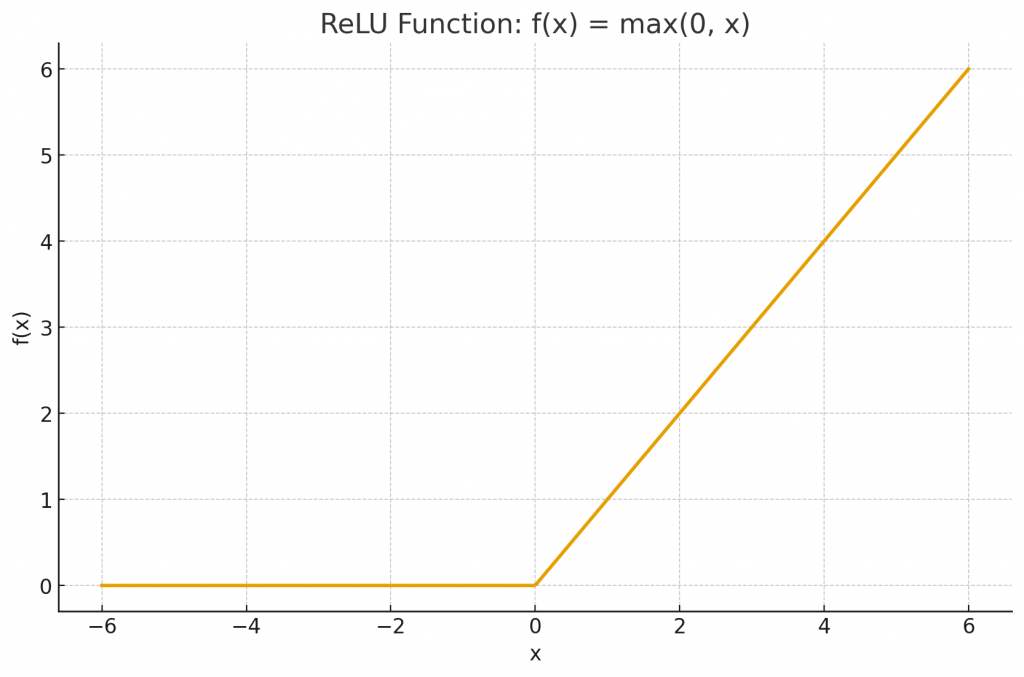

在上一章節提到的階梯函數中，由於在 0 的位置不可微，會導致在反向傳播過程中導數非常小甚至為 0。這樣一來，梯度在逐層傳遞時會不斷縮小最終幾乎消失。這種情況被稱為 梯度消失（vanishing gradient）。當梯度消失時，前層的權重幾乎無法更新，使得神經網路難以學到有效的特徵，讓我們先看看ReLU的公式。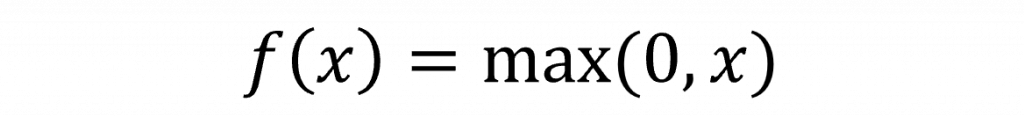

在這一個公式中，它的導數x>0 時為 1，在 x≤0 時為 0，這表示在正區域中，梯度不會趨近於 0，能有效避免梯度消失問題，這時我們輸入層->隱藏層(使用ReLU)的公式是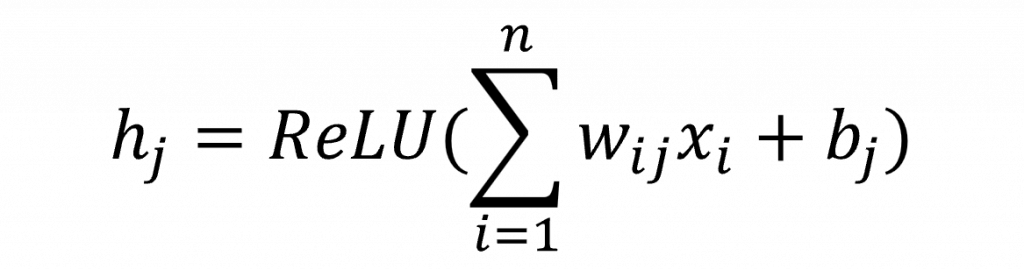

2.隱藏層->輸出層

而在隱藏層到輸出層時，常依任務性質選擇不同的激活函數，若是二分類問題，通常使用 sigmoid，因為它能將輸出壓縮到 (0,1)，自然解釋為正類的機率；若是多分類問題，則會使用 softmax，因為它能將輸出轉換成一個總和為 1 的機率分布，表示樣本屬於每一類的相對可能性。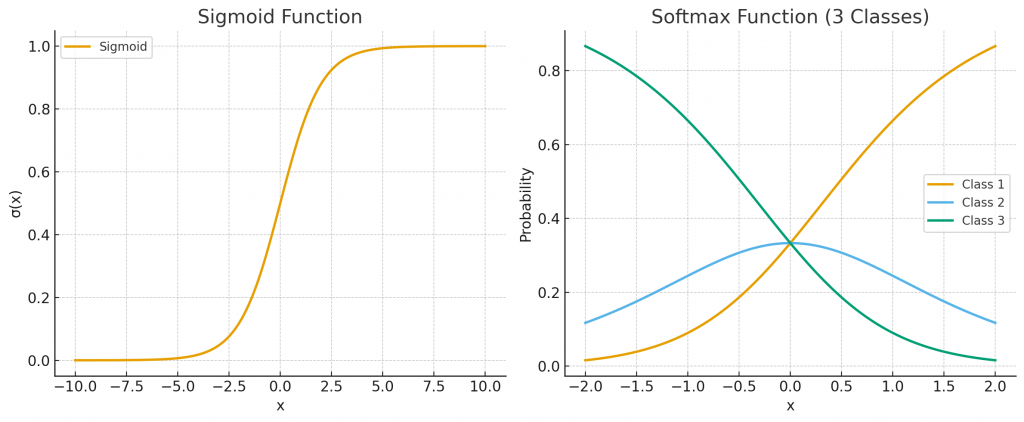

在圖片中我們可以直觀的看到左邊是 Sigmoid 函數，輸入在 (−10,10) 區間，輸出壓縮在 (0,1)；右邊是 Softmax 函數，模擬三個類別的輸出，可以看到隨著輸入變化，三個類別的機率會動態分配，且總和始終為 1。兩者對應的公式如下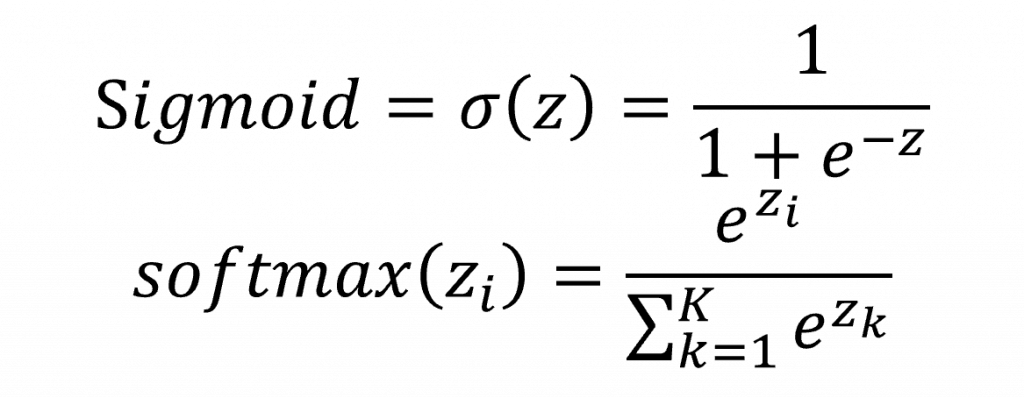

而在這裡我們使用Sigmoid，因此我們的隱藏層到輸出層的數學公式可以寫成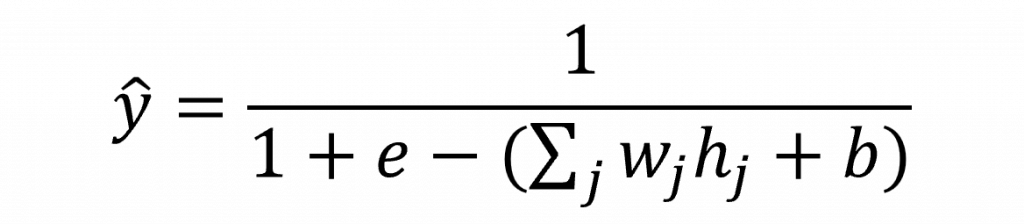

多層感知器的反向傳播

在前巷傳播中我們的流程是輸入層(x)->隱藏層(h)->隱藏層激勵函數(a)->輸出層(z)->輸出層激勵函數(y)->損失函數，因此我們在反向傳播時需要將這個返回來計算，因此讓我們看看第一步，在這裡我們損失函數同樣是MSE Loss

1. 損失函數對輸出層激勵函數

首先計算損失對輸出層輸出的偏導，這一步是誤差的來源，代表我們要最小化的方向。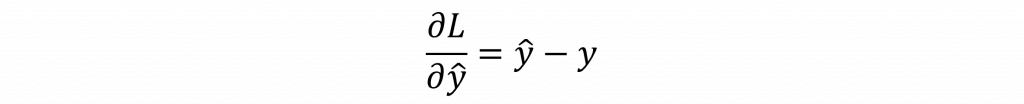

2. 損失函數對輸出層權重

接下來透過連鎖率展開，其中我們會使用到上一層的偏導結果。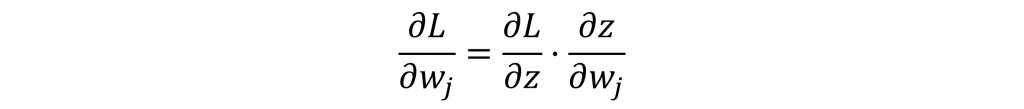

3. 損失函數對隱藏層激勵函數

誤差往前傳，會傳到隱藏層激勵輸出(a)，這是輸出層誤差「回流」給隱藏層的梯度。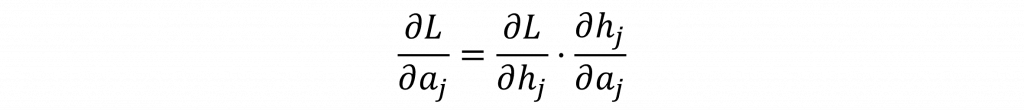

4. 損失函數對隱藏層權重

同樣使用連鎖率展開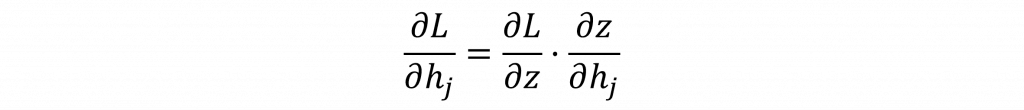

5. 損失函數對輸入層權重

如果前面還有更深的層，誤差會繼續往前傳，形式會一直套用這就是「誤差反向傳遞」的一般公式。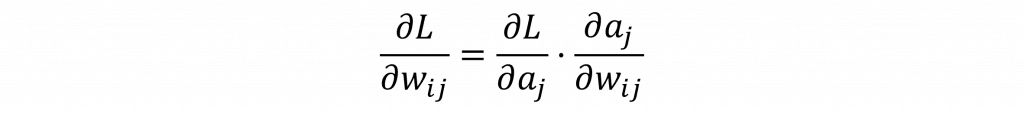

6.結合上述展開

總結來說整個誤差傳遞可以用以下公式表示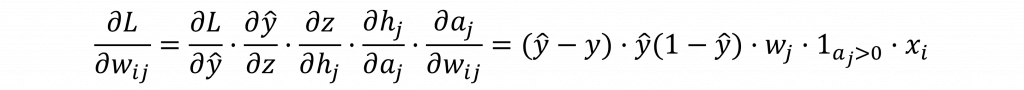

這樣就得到了完整的反向傳播公式。其實你會發現我們只是將前向傳播的流程反過來計算，並一步步地帶入各個結果。當你理解了這一點後，就能夠自行推導出各種 AI 模型的傳播與訓練過程。

下集預告

今天我們透過數學公式與推導，完整的了解多層感知器的前向傳播與反向傳播流程，理解了梯度如何一層層回傳，讓模型能逐步修正權重。明天我將帶你實際用程式碼一步步實現這個過程，這時你將會發現，數學公式與程式碼是一一對應的，當理解了推導之後，實作就只是把公式「翻譯」成程式語言。到時候你會真正體會到模型是如何一步步學會的。