題目介紹:
這題要求我們找出一棵二元樹（Binary Tree的最大深度，也就是從根節點（Root）到最遠葉節點（Leaf）的最長路徑所包含的節點數。換句話說，我們需要計算這棵樹有多少層。
觀念:
給定輸入為一個二元樹的根節點 root，輸出則是一個整數，表示這棵樹的最大深度。
為了達成這個目標，我們可以使用：
1.遞迴（DFS）：分別計算左右子樹的深度，取最大值再加 1。
2.迭代（BFS）：利用佇列進行層序遍歷，逐層計算深度。
程式碼及成功畫面截圖: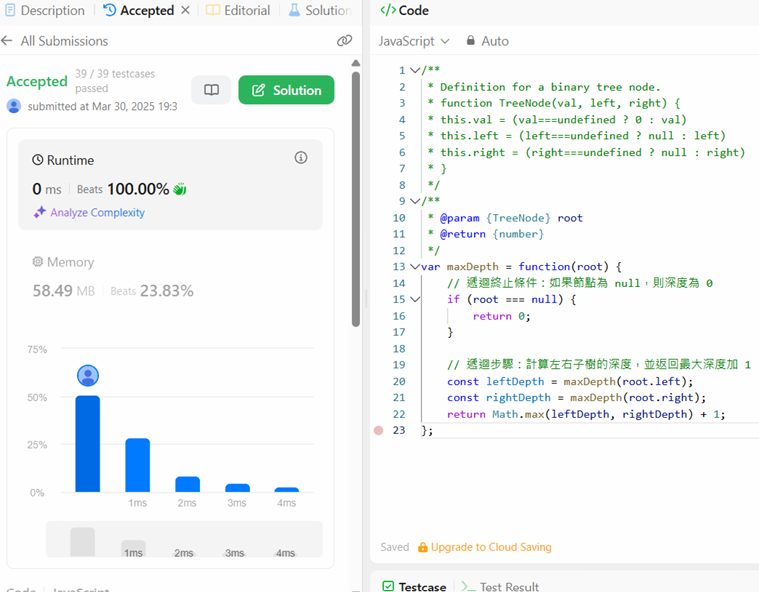

學習心得:
題目雖然看似簡單，但實際操作後會發現遞迴的精髓在於「將問題拆解到最小單位」，最後再往上累積答案。同時，藉由比較 DFS 與 BFS 的方法，我學到不同演算法各有優勢：DFS 程式簡潔直觀，而 BFS 更能直觀地看出層級關係。這題讓我體會到熟悉多種思路能讓解題更靈活。
延伸邏輯時事面:
1.教育學習
學生的學習歷程就像一棵樹，每一層代表不同階段的知識積累。學習的「深度」取決於是否持續往下鑽研，而不是只停留在表面。
2.組織結構
企業或政府的層級也像一棵樹。最大深度代表決策傳遞的層數。層級過深，可能導致溝通效率降低；層級適中，則能保持靈活與穩定。
3.人工智慧（AI）發展
類神經網路（Neural Network）的深度與這題的概念相似。模型層數越深，代表能學到更複雜的特徵，但同時也會帶來運算成本與過擬合的挑戰。