5. Longest Palindromic Substring

這題的目標是從給定的字串中，找到最長的那個「子字串」，而且那個子字串必須為「迴文」。

這題有幾個名詞需要解釋，1.迴文：是指一個正著讀或反著讀都一樣的的字串，例如：”level”、”madam”、”aba”。2.子字串，這名詞我在Day3的文章有解釋過，不在贅述。以這題的範例1 s = “babad”來說：它的迴文子字串有"b”、"a”、”d”、"bab"和"aba"，其中最長的是"bab"和"aba"。以範例2. s = “cbbd”來說：它的迴文子字串有"c"、"b"、"d"和"bb"，其中最長的是"bb"。

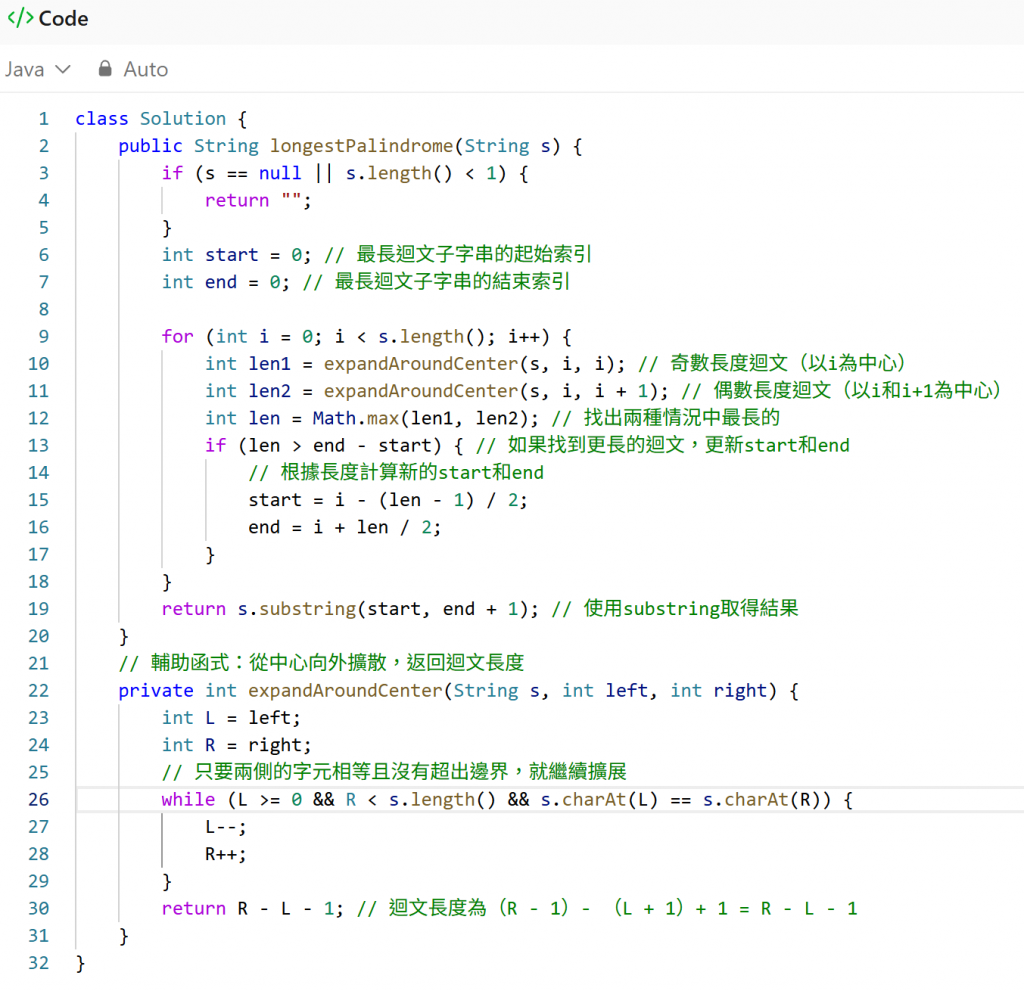
這題的解題思路是使用「中心擴散法」（Expand Around Center），這也是最常見最有效的方法。這個方法的核心思想是：一個迴文子字串，必定有一個中心點。對於每個中心點，分別以奇數長度和偶數長度兩種情況向兩側擴展，檢查是否為迴文。每次擴展時，比較當前的最長迴文子字串，如果找到更長的，就更新它。

這方法的具體操作是：假設字串長度為n。遍歷i從0到n - 1。對於每個i，會分成兩種情況討論，情況1.（奇數長度）：以i為中心，從s[i]向兩側擴展，比較s[i - 1]和s[i + 1]、s[i - 2]、s[i + 2]...，直到兩側的字元不相等或超出字串邊界為止。情況2.（偶數長度）：以ｉ和ｉ+1為中心，從s[i]和s[i + 1]開始向兩側擴展，比較s[i - 1]和s[i + 2]、s[i - 2]和s[i + 3]...，直到兩側的字元不相等或超出字串邊界為止。

這個方法的時間複雜度是O(n^2)，空間複雜度是O(1)。