10. Regular Expression Matching
    這是一個關於正規表達式匹配的問題，通常可以使用動態規劃（Dynamic Programming, DP）來解決。
    這題的核心概念是將一個大問題分解成一系列較小的、相互關聯的子問題，並儲存每個子問題的解，避免重複計算。
    如同前面所說，這題的解題思路是利用利用動態規劃，具體來說，可以使用一個二維布林陣列 dp來儲存子問題的解。其中，dp[i][j]表示s的前i個字元（s.substring(0, i)）是否能被p的前j個字元（p.substring(0, j)匹配。i的範圍是從0到s.length( )，而j的範圍是從0到p.length( )，這意味著dp這列的大小將是(s.length( ) + 1) x (p.length( ) + 1)。

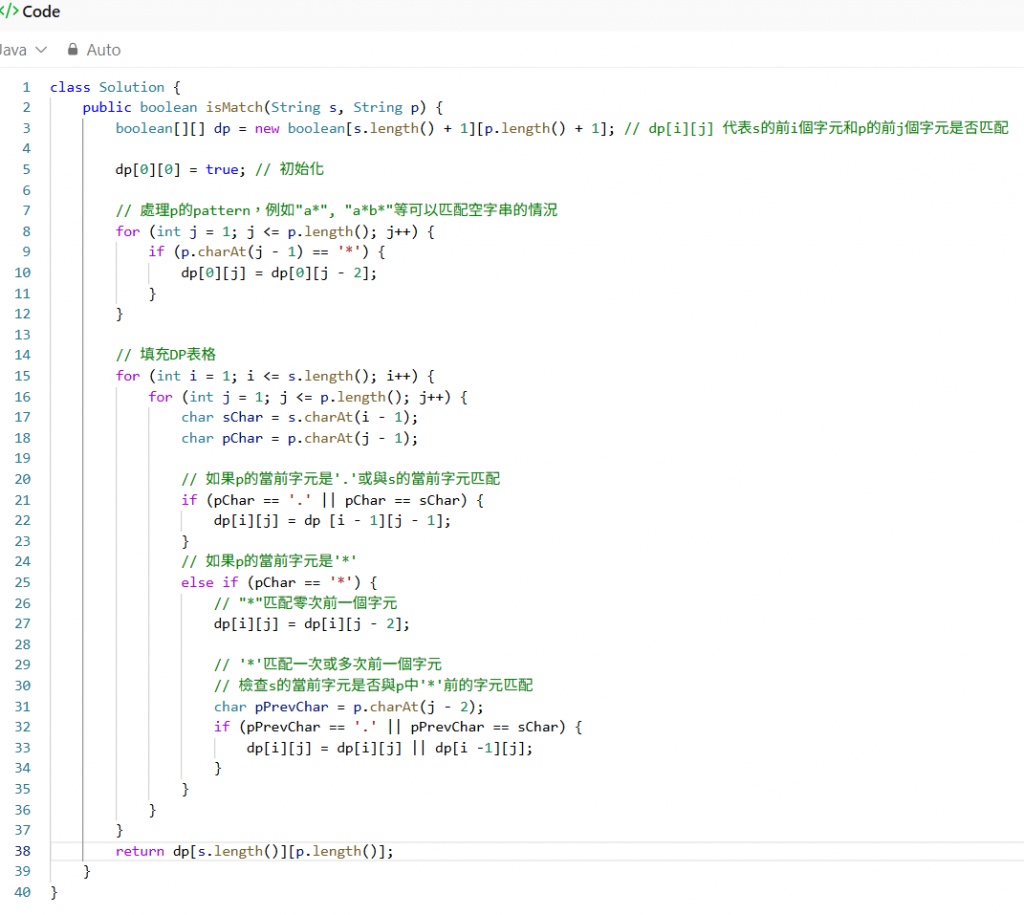
初始化是第一步。Dp[0][0]被設為true，因為兩個空字串（s的前0個字元和p的前0個字元）是匹配的。接著，需要考慮p模式能匹配空字串的特殊情況。如果p模式是a*, bc這類形式，它們可以通過匹配零次來「消失」。因此，如果p的第j - 1個字元是’*’，dp[0][j]的值會與dp[0][j - 2]相同，這表示p模式的前j個字元可以透過忽略p[j - 2]和p[j - 1]來匹配空字串。

再來，是核心的狀態轉移邏輯，從i = 1和j = 1開始，逐步填充整個dp表格。每次填充dp[i][j]時，根據p的j - 1個字元來判斷情況一或是情況二。如果是情況一：p[j - 1]是普通字元（或 ‘.’），p的當前字元既不是’’或是’.’這個萬用字元，匹配條件很直觀。dp[i][j]為 true的前提是s的前一個字元能與p的前一個字元匹配（s[i - 1] == p[j - 1]或p[j - 1] == ‘.’），且s的前i - 1個字元與p的j - 1個字元已經成功匹配（也就是dp[i - 1][j - 1]為true）；如果是情況二：p[j – 1]是’’，這是最複雜但也最關鍵的部分。''符號可以代表其前一個字元出現零次或多次，必須同時考慮這兩種可能性。假如是匹配零次的情況：p的’’及其前面的字元p[j - 2]可以被完全忽略，只需要判斷s的前i個字元是否能與p的前j - 2個字元匹配。因此，dp[i][j]的值取決於dp[i][j - 2]；假如是匹配一次或多次的情況：s的當前字元s[i - 1]必須與p的’’前面的字元p[j - 2]相匹配。如果它們匹配，就可以延續之前的匹配狀態。具體來說，s的前i - 1個字元已經能與p的前j個字元匹配（dp[i - 1][j]為true），現在s多出一個字元，而p的’’也能繼續匹配它。
綜合來看，當p[j - 1]是’’時，dp[i][j]的值是上述兩種情況的聯集（邏輯或）。完整的狀態轉移方程式為：dp[i][j] = dp[i][j – 2] || ((s.charAt(i - 1) == p.charAt(j - 2) || p.charAt(j - 2) == ‘.’) && dp[i - 1][j]，這個公式簡潔地涵蓋了’’匹配零次（dp[i][j - 2]）和匹配多次（dp[i-1][j]）的所有可能性。通過逐一填寫這個dp表格，最終dp[s.length( )][p.length( )]的值就是最終答案，它決定了整個s字串是否與整個p模式相匹配。