現在做資料分析或機器學習,選模型這件事真的很重要。除了那些大家常聽到的分類、回歸這類基本模型,其實還有一種比較特別的模型,它專門拿來處理時間序列資料。
這類資料的特性在於,數據之間是有時間順序的,前後資料會互相影響不是單純的靜態資訊。像是股票走勢、氣象預報,甚至是病患的心跳紀錄甚至是文字,都是典型的時間序列。如果用傳統模型來處理這些資料,往往會忽略時間的關聯性,導致效果不佳。所以這些專門為時間序列設計的模型就變得越來越重要,也越來越常被拿來解決這類問題。而今天我就會來告訴你該怎麼從DNN延伸到時間序列模型
在我們日常生活中最常見的時間資料就是文字,因為文字是有順序、有上下文的,簡單來說,前面出現的詞會影響後面詞的理解。想要讓模型搞懂這種時間上的連續性,我們得用一種會記憶的網路結構,而 RNN(Recurrent Neural Network)就是基於這一點而成的。
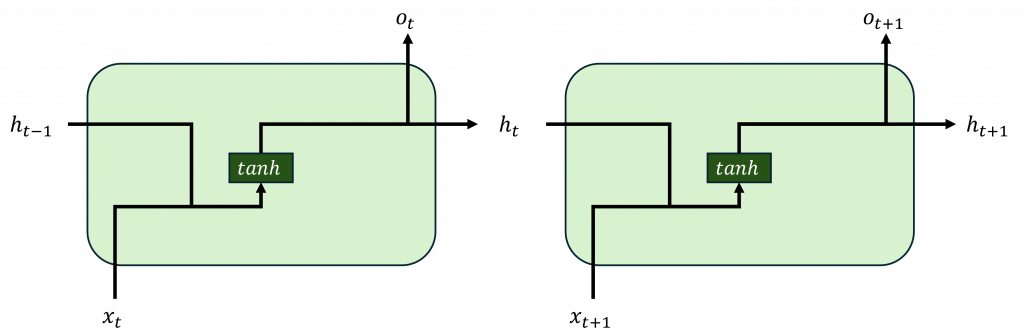
RNN 的核心想法其實不難,它用一個叫 隱藏層狀態(hidden state) 的東西,把前面時間步的資訊傳到下一步。每看到一個詞,就把它轉成向量,再結合上一個隱藏層狀態做些運算,更新出新的隱藏層狀態,你可以把它想成是一張小小的便條紙,從句子開頭一路寫到結尾,記錄下語意的脈絡。
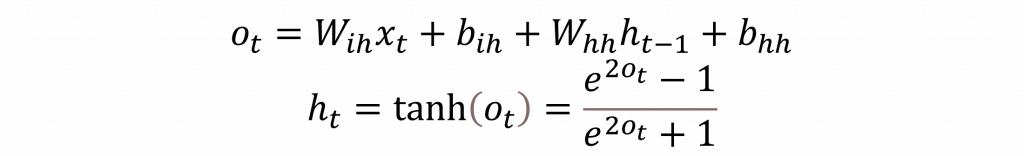
當我們從數學的角度來看這個過程,可以把它拆成兩個部分第一部分是計算當前時間點的輸入 x(t),而第二部分則是處理之前幾個時間點所累積的隱藏層狀態。這兩個結果會被結合起來,然後透過 tanh 這個激勵函數把值壓縮在 -1 到 1 之間。簡單來說就是把輸入和保留下來的記憶狀態拿來做一個 Wx 加上 b 的運算。
在這裡我們使用 nn.Linear 來自行建造一個 RNN 模型,讓你更直觀地理解數學概念:
class LinearTanhRNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super().__init__()
# 輸入 -> 隱層
self.i2h = nn.Linear(input_size, hidden_size, bias=True)
# 前一隱狀態 -> 隱層
self.h2h = nn.Linear(hidden_size, hidden_size, bias=True)
# 隱層 -> 輸出
self.h2o = nn.Linear(hidden_size, output_size, bias=True)
self.hidden_size = hidden_size
首先我們理解一下數學公式,在每一層輸入的 o(t) 都是由 i2h 與 h2h 這兩個 Wx+b 運算構成的,因此我們首先要定義這兩個 nn.Linear。而最終的輸出通常會在最後加入一個 h2o,這個作法是為了將整個複雜的網路做線性運算,這和我們在 CNN 結尾接上全連接層的概念是一樣的。
def forward(self, x, h0=None):
B, T, _ = x.shape
# 初始化隱狀態
h = x.new_zeros(B, self.hidden_size) if h0 is None else h0
for t in range(T): # 逐時間步展開
# 線性累加後做 tanh 非線性
h = torch.tanh(self.i2h(x[:, t, :]) + self.h2h(h))
# 輸出層:將最後隱狀態投影到目標維度
y_last = self.h2o(h)
return y_last, h
在前向傳播方面,我們需要初始化一個隱狀態的單元,這個單元會提供模型初始的隱藏資訊(畢竟在 x(0) 的時候還沒有任何記憶)。接著我們用一個 for 迴圈,逐步取出時間序列的每個時間步進行運算。由於我們的輸入是三維的(batch_size, seq_len, feature),所以使用 seq_len 作為時間長度進行迴圈運算。這個流程就是最簡單的時序模型原型。
LSTM 可以把它想成替 RNN 裝上一條能長距離搬運訊息的「傳送帶」,名字叫 cell state。每一步模型先決定要把舊資料擦掉多少,再決定新東西要不要寫進傳送帶,最後才決定當下要露出哪一部分當成輸出。因為 cell state 的更新以加法為主,不是層層相乘,所以重要訊號不會在長序列裡被稀釋到幾乎看不見,梯度也比較能往回傳。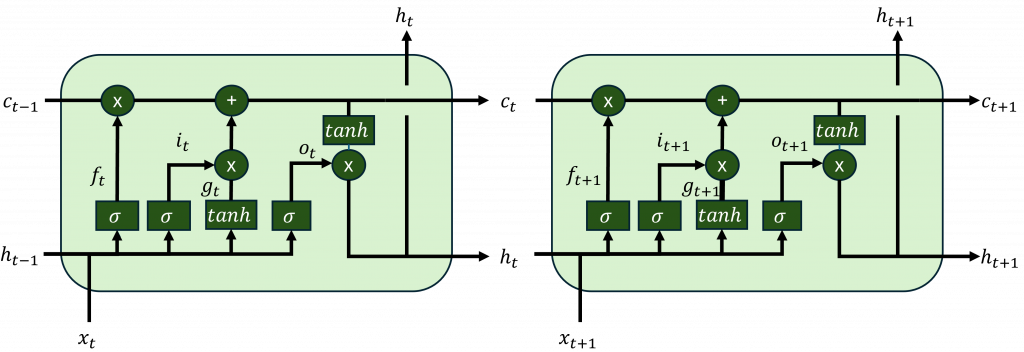
直觀地說,追劇追到第十季時,你不會把第一季的所有細節硬背在腦中而是留下一本長期筆記。每一集先把過時的備註劃掉再把新的劇情補進去,輪到要回答朋友問題時才翻出相關段落。LSTM 就是把這三步學起來忘多少、寫多少、秀多少。對應到數學式就是先算出三個 0 到 1 的比例,再用一個候選內容去更新筆記,最後把更新後的筆記過一層非線性變成當前的隱狀態,他基本上可以歸類以下幾個元件。
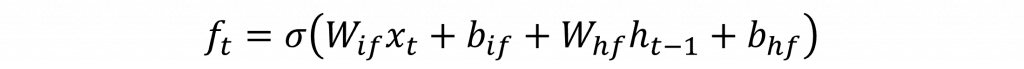
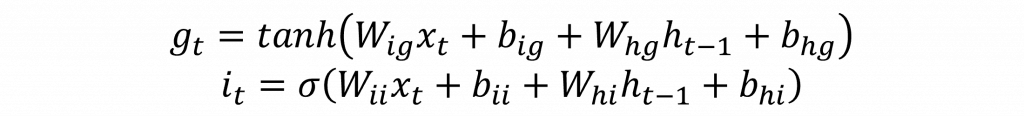
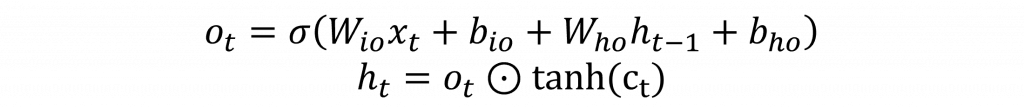
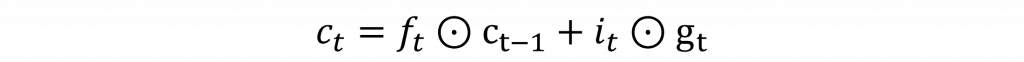
nn.Linear()展開,讓你更直觀的理解LSTM在做些什麼。import torch
import torch.nn as nn
import torch.nn.functional as F
class LinearTanhLSTM(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super().__init__()
H = hidden_size
# x 路徑(含 bias_ih)
self.x_i = nn.Linear(input_size, H, bias=True)
self.x_f = nn.Linear(input_size, H, bias=True)
self.x_g = nn.Linear(input_size, H, bias=True)
self.x_o = nn.Linear(input_size, H, bias=True)
# h 路徑(含 bias_hh)
self.h_i = nn.Linear(H, H, bias=True)
self.h_f = nn.Linear(H, H, bias=True)
self.h_g = nn.Linear(H, H, bias=True)
self.h_o = nn.Linear(H, H, bias=True)
# 輸出層
self.h2o = nn.Linear(H, output_size, bias=True)
self.hidden_size = H
用程式碼讀起來也很直白,每個時間步把輸入 x 和前一刻的隱狀態 h 各丟進四個線性層,得到四組向量,再套上 sigmoid 或 tanh。i 表示寫入比例,f 表示遺忘比例,g 是候選內容,o 決定要輸出多少。
def forward(self, x, h0=None, c0=None):
B, T, _ = x.shape
H = self.hidden_size
device = x.device
h = torch.zeros(B, H, device=device) if h0 is None else h0
c = torch.zeros(B, H, device=device) if c0 is None else c0
for t in range(T):
xt = x[:, t, :]
i = torch.sigmoid(self.x_i(xt) + self.h_i(h))
f = torch.sigmoid(self.x_f(xt) + self.h_f(h))
g = torch.tanh( self.x_g(xt) + self.h_g(h))
o = torch.sigmoid(self.x_o(xt) + self.h_o(h))
c = f * c + i * g
h = o * torch.tanh(c)
y_last = self.h2o(h)
return y_last, (h, c)
而其餘計算也與RNN相似,差別在於要將cell state與隱狀態更新也就是c = f*c + i*g,h = o*tanh(c)。這樣一來關鍵資訊可以沿著 c 這條通道跨很多步而不崩壞,h 則負責提供當下的可見表徵,同樣地最後丟進 h2o 產生你要的輸出大小即可。
而LSTM最大的問題其實就是運算速度過慢,每一個 cell 都要等上一個 h_t, c_t 算完才能動,等於把整條序列綁在一個長 for 迴圈裡,而GPU 最怕這種細碎依賴鏈很長的工作,每步只做幾個中小型矩陣乘法,且核心限制仍在「下一步必須等上一步」,因此後續雖然有著結構相似用於改善速度的GRU,但種結構性問題是沒辦法解決此類問題的。
明天我們將運用今天介紹的 LSTM 模型,來捕捉句子中那些細微卻關鍵的語意轉折。你將看到一段文字如何被模型逐層拆解、理解,再被重組成一種「機器的詮釋」。這將引領你正式踏入自然語言處理(NLP)的領域,並親手構建一個情緒分析器,體驗從數據到洞察的完整流程。
