12. Integer to Roman

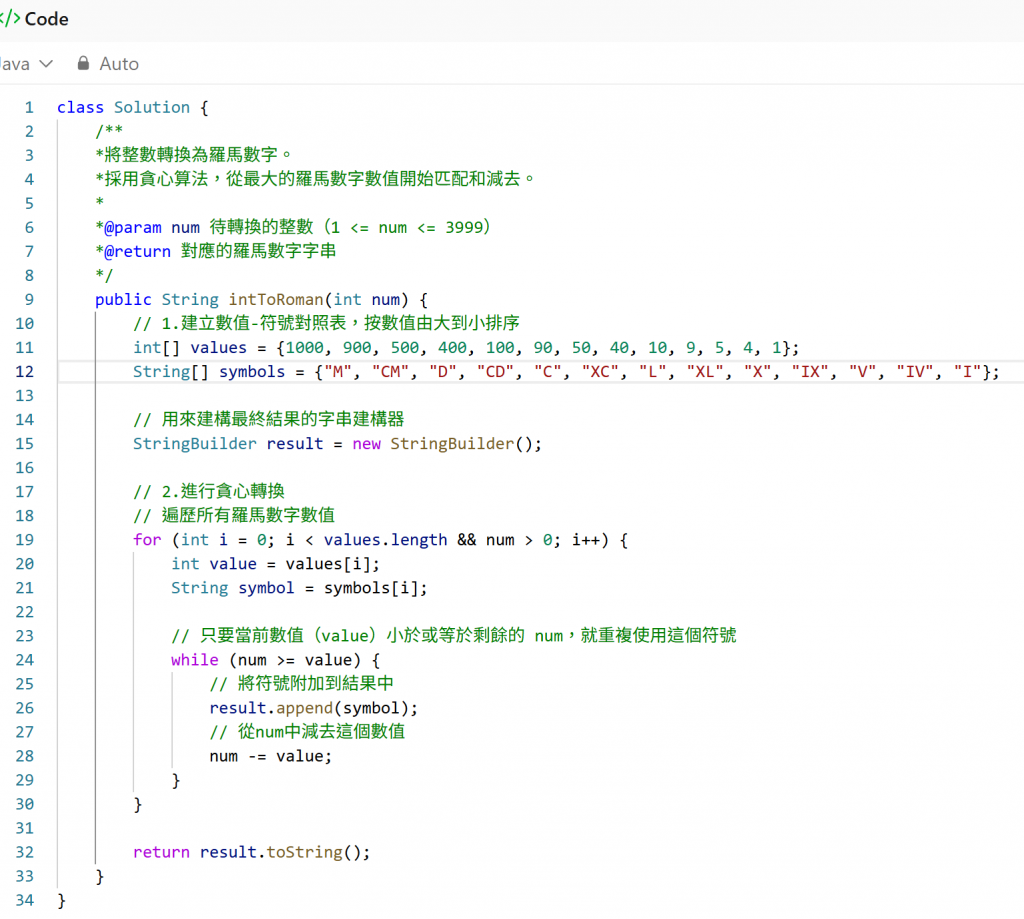
這題要求將一個給定的整數（範圍在1到3999之間）轉換成對應的羅馬數字表示。

要解開這題，要先了解羅馬數字的規則，羅馬數字的轉換規則是基於十進制位值（個位、十位、百位、千位）來進行的，並從最高位開始轉換。

主要的符號及其數值：

I -> 1 C -> 100

V -> 5 D -> 500

X -> 10 M -> 1000

L -> 50

羅馬數字的形成原則有三條：1.最大值原則（從大到小），通常情況下，羅馬數字是透過將較大數值的符號放在較小數值的符號前面，來表示數值的相加。例如：6 = 5(V) + 1(I) = VI；20 = 10(X) + 10(X) == XX。
2.重複原則：只有I, X, C, M（10的冪次）可以連續重複，但最多只能重複三次。例如：3 = III；300 = CCC。符號V, L, D（5的倍數）不能重複使用。
3.減法原則（特殊情況：4和9）：為了避免4個連續重複（例如4不寫成IIII），以及表示9的情況，會使用減法形式。減法形式是將一個較小的符號放在一個較大的符號前面，表示兩者數值相減。

只允許以下六種減法組合：

4: IV（5 - 1）

9: IX（10 - 1）

40: XL（50 -10）

90: XC（100 - 10）

400: CD（500 - 100）

900: CM（1000 - 100）

重點在於轉換是按位元進行的。例如3749必須拆分成3000 + 700 + 40 + 9，然後分別轉換並串接：

3000 -> MMM

700 -> DCC（500 + 100 + 100）

40 -> XL

9 -> IX
結果：MMMDCCXLIX

這題的解題方法是使用貪心算法（Gready Algorithm），從最大的羅馬數字數值開始，不斷地減去能匹配的最大值，直到原數字歸零。
首先先建立符號/數值對照表，將所有可能的數值（包括10的冪次、5的倍數，以及4和9的特殊減法形式）及其對應的羅馬符號配對，並按照數值由大到小的順序排列。

1000 -> M 100 -> C 10 -> X 1 -> I

900 -> CM 90 -> XC 9 -> IX

500 -> D 50 -> L 5 -> V

400 -> CD 40 -> XL 4 -> IV

建立完後，就可以使用貪心算法進行轉換，從對照表的最大數值開始，對於給定的輸入數字num進行以下動作：
1.檢查當前數值（value）是否小於或等於num。

2.如果是，表示這個羅馬符號（symbol）可以用來表示num的一部分。將這個符號附加到結果字串中，並將num減去這個數值。

3.重複步驟1.和2.，直到當前數值不再小於或等於num，然後才移動到對照表中的下一個較小的數值。

4.重複以上步驟，直到num變為0。

這個方法之所以有效，是因為預先包含了4, 9, 40, 90, 400, 900這些減法形式，確保總是選擇能匹配的最大有效羅馬數字組合。