
在研讀Learn You a Haskell for Great Good這本書的時候,作者介紹了Zipper這個有趣的資料結構,今天要用fp-ts來實作其中的內容和範例。
由於函數式程式設計要求引用透明性(Referential transparency)和不可變性(Immutable),當我們要修改樹中某個位置的值,我們必須重新輸出一棵樹,因此一切變得相當麻煩。我們先以較特別的二元樹來進行說明,先建構下圖中二元樹。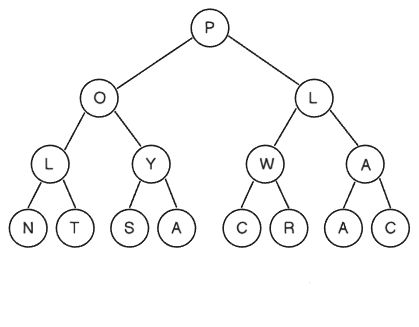
import { fold, make, Tree } from 'fp-ts/Tree';
const t: Tree<string> = make('P', [
make('O', [
make('L', [make('N'), make('T')]),
make('Y', [make('S'), make('A')]),
]),
make('L', [
make('W', [make('C'), make('R')]),
make('A', [make('A'), make('C')]),
]),
]);
如果我們想將右樹中的'W'改為'P',我們要設計一個函數changeToP接受二個參數,第一個參數是抵達'W'的路徑,第二個參數是我們的樹t,輸出則是一棵新樹,這個新樹的結構和原樹t一樣,只是'W'被改為'P'。我們先做以下的型別設計和常數定義,Directions型別做為我們changeToP的第一個參數型別,代表到達目的節點的路徑。
type Direction = 'Left' | 'Right';
type Directions = Direction[];
const L: Direction = 'Left';
const R: Direction = 'Right';
const ds: Directions = [R, L]; // 從根目錄到'W'的位置要先到右樹(R),再往左樹(L)
如此我們便可用遞迴設計我們的changeToP,基礎情況是當路徑參數是空陣列時(第一個元素是undefined時),表示已經到達目的節點,此時即可回傳一棵節點值為'P',子樹不變的的新樹;若路徑參數不是空陣列時,則取出第一個元素(head),則回傳的新樹節點值不變,若head為L,則回傳子樹的右樹取原來的右樹,左樹則用changeToP遞迴建立;head為R,則回左樹不變,右樹用changeToP遞迴建立。
type ChangeToP = ([head, ...tail]: Directions) => (t: Tree<string>) => Tree<string>;
const changeToP: ChangeToP =
([head, ...tail]) =>
(t) => {
const [l, r] = t.forest;
return head === undefined
? make('P', [l, r])
: head === L
? make(t.value, [changeToP(tail)(l), r])
: make(t.value, [l, changeToP(tail)(r)]);
};
console.log(changeToP(ds)(t))
這個方法似乎可行,但是當我們所要操作的樹非常龐大,路徑參數是很長的陣列,而且需要一直不停的改變我們的樹,這個方法便顯得非常沒有效率,因為我們每一次都要從根路徑開始由上而下的走過我們的樹,如果我們希望不要每一次都從頭來過,我們可以利用Zipper這種資料結構讓我們能自由的在樹中來回移動。
當我們在一個複雜的森林行走時,如果要能安全循原路走回去,一個有效的方法是延著我們走的路徑灑下麵包屑,這樣我們便可以隨著我們灑下的麵包屑徑往回走。而我們Zipper結構中重要的元素便是稱為麵包屑(Breadcrumbs)的資料結構,Crumb是一個包含方向、節點值和另半棵樹所形成的元組,Breadcrumbs則是Crumb所組成的陣列,它包含了我們要回頭的所有資訊,而Zipper便是由要往下走的子樹Tree和回頭的資訊Breadcrumbs所組成的元組,很明顯的,Zipper是一棵樹的完整地圖,也就是說無論我們無論在樹的那個節點位置,隨時都有整棵樹的資訊。
type Crumb<A> = [Direction, A, Tree<A>];
type Breadcrumbs<A> = Crumb<A>[];
type Zipper<A> = [Tree<A>, Breadcrumbs<A>];
有了Zipper這個資料結構,接下來我們要定義goLeft、goRight和goTop三個函數,這三個函數的輸出入都是Zipper的型別,因此我們定義了Go的型別Zipper<A> -> Zipper<A>,但是由於如果我們所在的節點已經沒有左子樹(右子樹),goLeft(goRight)便會失敗;而所在的節點是根節點,goTop也會失敗,因此將Go型別的輸出型別調整為Option<Zipper<A>。
import {
Option,
some,
none,
flatMap,
getOrElseW,
match,
} from 'fp-ts/Option';
type Go<A> = (tb: Zipper<A>) => Option<Zipper<A>>;
我們先將Zipper<A>解構為[ { value, forest: [l, r], }, bs, ],如果有左子樹,goLeft要回傳的Zipper是[l, [[L, value, r], ...bs]],因為可能失敗,所以用Option的建構函數some封裝;如果沒有子樹則回傳none,goRight則恰好相反。
const goLeft: Go<string> = ([
{
value,
forest: [l, r],
},
bs,
]) => (l === undefined ? none : some([l, [[L, value, r], ...bs]]));
const goRight: Go<string> = ([
{
value,
forest: [l, r],
},
bs,
]) => (r === undefined ? none : some([r, [[R, value, l], ...bs]]));
goTop的時候,因為需要Breadcrumbs中的第一筆資訊重建輸出Zipper中的Tree,所以將Zipper<A>解構為[focus, [[d, x, t], ...restBs]],如果d是L,focus當左樹,t當右樹;如果d是L則相反;如果d沒有定義,表示Breadcrumbs是空陣列,已經在根節了,所以回傳none。
const goUp: Go<string> = ([focus, [[d, x, t], ...restBs]]) =>
d === undefined
? none
: d === L
? some([make(x, [focus, t]), restBs])
: some([make(x, [t, focus]), restBs]);
如果我們想在任何節點都能直接回到根節點,便要用topMost來完成,topMost是遞迴函數,基礎情況是已經在根節點,其它情況則往回一層。
const topMost: Go<string> = (
zp // zp = [item, bs]
) => (zp[1].length === 0 ? some(zp) : pipe(zp, goUp, flatMap(topMost)));
用這四個函數,我們可以在二元樹中任意移動。
const newFocus = pipe(
some([t, []]), // 起始狀況在根節點
flatMap(goLeft),
flatMap(goLeft),
flatMap(goRight),
getOrElseW(() => 'Failure')
);
我們想在樹的某個節點修改該節點的資料必須要有modify函數,modify的參數是型別A到型別A的函數,用來改變節點的值,modify(f)是一個Go型別的函數,實作如下:
const modify =
<A>(f: (x: A) => A) =>
([t, bs]: Zipper<A>): Option<Zipper<A>> =>
t === undefined
? none
: some([{ value: f(t.value), forest: t.forest }, bs]);
我們最後一個函數是attach,它的參數是Tree<A>型別t,attach(t)也是Go型別的函數
const attach =
(t: Tree<string>) =>
([_, bs]: Zipper<string>): Zipper<string> =>
[t, bs];
綜合以上的函數,可以在樹中任意遍歷和修改節點值或替代正在focus的樹,下列程式碼可以意註解管道中的函數,觀察不同的結果。
const newFocus = pipe(
some([t, []]),
flatMap(goLeft),
flatMap(goLeft),
// flatMap(goLeft),
flatMap(goRight),
// flatMap(goLeft),
flatMap(topMost),
// flatMap(goLeft),
flatMap(modify((x) => 'Z')),
// modify((x) => 'Z'),
// map(modify((x) => 'Z')),
// map(attach(make('U', []))),
getOrElseW(() => 'Failure')
);
Zipper也可以應用在非樹的結構上,檔案系統就是很好的例子。檔案系統主要由檔案和目錄構成,我們用以下的物件分別做為檔案和目錄的型別。
type Name = string;
type Data = string;
type FileItem = {
type: 'File';
name: Name;
value: Data;
};
type FolderItem = {
type: 'Folder';
name: Name;
value: FSItem[];
};
type FSItem = FileItem | FolderItem;
接下來我們要討論是什麼構成Crumb的要素。首先我們的focus必然是目錄,因此當往上移要重建目錄時必須要有這個目錄之前的所有檔案和目錄+現在這個目錄+這個目錄之後的所有檔案和目錄,而重建目前的目錄的FolderItem只需要name,因此Crumb的組成會是[ 目錄名, 之前的所有檔案和目錄, 之後的所有檔案和目錄 ]這樣的元組,FSCrumb和FSZipper的型別定義如下:
type FSCrumb = [Name, FSItem[], FSItem[]];
type FSZipper = [FSItem, FSCrumb[]];
假設我們磁碟目錄如下組成。
const myDisk: FSItem = {
type: 'Folder',
name: 'root',
value: [
{
type: 'File',
name: 'goat_yelling_like_man.wmv',
value: 'baaaaa',
},
{
type: 'File',
name: 'pope_time.avi',
value: 'god bless',
},
{
type: 'Folder',
name: 'images',
value: [
{
type: 'File',
name: 'image1.jpg',
value: 'I am image1!',
},
{
type: 'File',
name: 'image2.png',
value: 'I am image2!',
},
{
type: 'File',
name: 'image3.bmp',
value: 'I am image3!',
},
],
},
{
type: 'File',
name: 'Just.doc',
value: 'Just doc file',
},
{
type: 'Folder',
name: 'language',
value: [
{
type: 'File',
name: 'tutor1.hs',
value: 'Maybe a function',
},
{
type: 'File',
name: 'tutor2.jsx',
value: 'I am a react component',
},
{
type: 'File',
name: 'tutor3.py',
value: 'I am a python function',
},
],
},
],
};
當我們要從目前的目錄往下面的目錄移動時,我們要從目前目錄的value中找到往下移目錄的name,然後再將所有的目錄和檔案分成目前目錄之前和目前目錄之後,因此我們需要nameIs和breakaway兩個函數(helpers),往下層目錄移動的函數fsTo的程式碼如下:
const nameIs =
(name: Name) =>
(item: FSItem): boolean =>
item.name === name;
const breakArray =
<A>(filter: (x: A) => boolean) =>
(ls: A[]) => {
const index = ls.findIndex(filter);
return [ls.slice(0, index), ls.slice(index)];
};
type FsTo = (name: Name) => (fsz: FSZipper) => FSZipper;
const fsTo: FsTo =
(name) =>
([item, bs]) => {
const { name: folderName, value: fsItems } = item as FolderItem;
const [ls, [target, ...rs]] = breakArray(nameIs(name))(fsItems);
return [target, [[folderName, ls, rs], ...bs]];
};
往上層目錄移動只需將FSCrumbs型別的第一個元素拿出來重新建構FSItem型別做為FSZipper的第一個元素,再把餘下的FSCrumbs當成新的FSCrumbs即可。
type FsUp = (fsz: FSZipper) => FSZipper;
const fsUp: FsUp = ([item, [[name, ls, rs], ...bs]]) => [
{ type: 'Folder', name, value: ls.concat([item]).concat(rs) }, // FSItem
bs, // FSCrumb[]
];
最後我們再完成替目錄更名(fsRename)和新增項目(fsNewItem)兩個函數
type FsRename = (name: Name) => (fsz: FSZipper) => FSZipper;
const fsRename: FsRename =
(newName) =>
([{ name, ...rest }, bs]) =>
[{ name: newName, ...rest }, bs];
const newFsFocus3 = pipe(
[myDisk, []],
fsTo('pope_time.avi'),
fsRename('pope.ave')
);
type FsNewItem = (item: FSItem) => (fsz: FSZipper) => FSZipper;
const fsNewItem: FsNewItem =
(item) =>
([folderItem, bs]) => {
const { value: items, ...rest } = folderItem as FolderItem;
return [{ value: [item].concat(items), ...rest }, bs];
};
const newFsFocus4 = pipe(
[myDisk, []],
fsTo('images'),
fsNewItem({
type: 'File',
name: 'newFile.jpg',
value: 'This is new image file',
})
);
這個簡易的檔案系統尚未考慮上下移目錄不存在和要改名目錄不存在的問題,可以再加上Option的型別容器讓它更安全,就留給大家當作練習。
Zipper像拉鏈一樣,可以往上往下拉。往下拉會將這一層的資訊分離,往上拉則能接合上層的資訊。Zipper來實作在樹中和檔案系統中上下移動的純函數,維持了FP中引用透明性(Referential transparency)和不可變性(Immutable)的要求。除了樹和檔案系統,Zipper的觀念也可以用來完成陣列的移動。今日的分享就到這邊告一段落,明天再見。
