
今天要介紹fp-ts/Tree模組。
樹是一種常見的圖形,由節點(node)和邊(edge)構成,樹會有一個根節點,根節點連著0或多棵子樹,因此樹的資料結構通常用遞迴定義,沒有子樹的節點稱為葉子(leaf)。fp-ts/Tree模組的樹是可以擁有多個子節的樹資料結構,它的介面定義如下:
export type Forest<A> = Array<Tree<A>>
export interface Tree<A> {
readonly value: A
readonly forest: Forest<A>
}
建構一顆樹的資料結構有以下幾個方法:
我們可以直接按照介面的定義建構樹的物件。
// Direct construction
const numberTree: Tree<number> = {
value: 1,
forest: [
{ value: 2, forest: [] },
{ value: 3, forest: [
{ value: 4, forest: [] },
{ value: 5, forest: [] }
]}
]
}
fp-ts也提供了make函數建立單一節點的樹,make有二個參數,第一個參數是節點的值;第二個參數是子樹陣列,如果沒有提供第二個參數,預設為空陣列,我們也可以用make函數建構一模一樣。
const numberTree: Tree<number> = make(1, [
make(2),
make(3, [
make(4),
make(5)
])
])
我們也可以透過unfoldTree函數遞迴建立一棵樹,unfoldTree函數的型別簽名如下:
unfoldTree: <A, B>(b: B, f: (b: B) => [A, Array<B>]): Tree<A>
unfoldTree函數需要二個參數,第一個參數是型別B的種子值(seed),第二個參數是節點生成函數,這個函數要回傳一個tuple,tuple的第一個值是樹節點的值,第二個值是型別B的種子值陣列,unfoldTree會根據這個陣列的種子值生成一個樹的陣列。下面的程式碼用unfoldTree生成一棵二元樹,每個節的值是所有子樹節點值的和,而每個子樹的節點值大約是父節點值的一半。這個函數的演算法必須要設立函數停止條件,也就是傳回空的種子值陣列。
const binaryTreeUnfold = T.unfoldTree(
10, // seed value
(n: number): [number, number[]] => {
if (n <= 1) {
return [n, []] // leaf node
}
const left = Math.floor(n / 2)
const right = n - left
return [n, [left, right]] // node with two children
}
)
Tree模組中當然也提供了map,ap,flatMap(chian)和of這幾個作為Monad類別必要的函數,map、flatMap和of的使用其它Monad沒有差異,就不浪費篇幅。Tree和Array一樣,存放不只一個值,因此它的ap的效果比較特別。我們先建立一個number型別的樹numberTree和一個只有根元素的數學函數樹mathFunctionsTree,看看pipe(mathFunctionsTree, ap(numbersTree))的結果。
// Tree of numbers
const numbersTree = make(3, [make(7), make(12, [make(8)])]);
// Tree of functions
const mathFunctionsTree = make(
(x: number) => x * 2,
[
make((x: number) => x + 10),
make((x: number) => x - 5, [make((x: number) => x / 2)]),
]
);
console.log(pipe(mathFunctionsTree, ap(numbersTree)))
mathFunctionsTree樹裏的每一個函數都會作用在numberTree樹中的每個元素而得到一棵樹,所得到便放在輸出的樹中相對應的位置。例如函數(x: number) => x * 2得到的樹放置根的位置,即等同於map((x: number) => x * 2)(numberTree),而
(x: number) => x + 10和(x: number) => x - 5得到的兩棵樹放在根節點的子樹,而(x: number) => x / 2得到的樹則放置在(x: number) => x - 5所產上的樹根節點的子樹上。因為執行結果比較冗長,這邊就不列出來,讀者可以自行將程式碼測試檢驗結果。
reduce,fold在Functional Programming互為別名(alias),因此功用是一樣的,在Array模組中只有reduce函數,在Tree模組中fold和reduce的使用方法略有不同,下面將這三個方法做說明。
reduce的使用彈性最大,它的使用方法和Array的reduce一樣,但是樹結構的深度優先遍歷(Depth-First Traversal DFT)有Preorder (先序), Inorder (中序), 和 Postorder (後序)三種,我們用下列程式碼可以了解fp-ts/Tree模組中reduce和reduceRight中使用遍歷的方法,numberTree2的樹狀結構如下圖所示: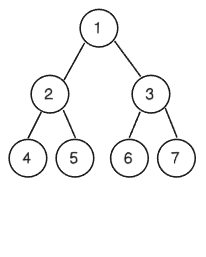
const numbersTree2 = make(1, [
make(2, [make(4), make(5)]),
make(3, [make(6), make(7)]),
]);
console.log(reduce([], (acc, ele) => [...acc, ele])(numbersTree2)); // left preorder [1,2,4,5,3,6,7]
console.log(reduce([], (acc, ele) => [ele, ...acc])(numbersTree2)); // right postorder [7,6,3,5,4,2,1]
console.log(reduceRight([], (ele, acc) => [...acc, ele])(numbersTree2)); // right postorder [7,6,3,5,4,2,1]
console.log(reduceRight([], (ele, acc) => [ele, ...acc])(numbersTree2)); // left preorder [1,2,4,5,3,6,7]
fold函數則會將先前fold好的結果放入陣列中
import { concatAll as concatAllM } from 'fp-ts/Monoid';
import { getMonoid } from 'fp-ts/Array';
type ConcatArray = (as: readonly number[][]) => number[]
const concatArray: ConcatArray = concatAllM(getMonoid<number>());
console.log(
fold((a: number, bs: Array<Array<number>>) => [...concatArray(bs), a])(
numbersTree2
)
); // left postorder [4,5,2,6,7,3,1]
console.log(
fold((a: number, bs: Array<Array<number>>) => [a, ...concatArray(bs)])(
numbersTree2
)
); // left preorder [1,2,4,5,3,6,7]
我們也可以不使用Monoid類別,直接用bs.reduce來處理,但是這樣就有些畫蛇添足了。
fold函數則強制使用Monoid類別,但是使用上也就加簡單。
import { MonoidSum } from 'fp-ts/number';
import { Monoid as MonoidString } from 'fp-ts/string';
console.log(foldMap(getMonoid<number>())((x: number) => [x])(numbersTree2)); // left preorder [1,2,4,5,3,6,7]
console.log(foldMap(MonoidSum)(identity<number>)(numbersTree2)); // 28
console.log(foldMap(MonoidString)((n: number) => String(n))(numbersTree2)); // '1245367'
drawTree可以Tree<string>轉換為表示樹結構的string。
console.log(
pipe(
numberTree,
map((n) => String(n)),
drawTree2
)
);
// 1
// ├─ 2
// │ ├─ 3
// │ └─ 4
// └─ 5
// ├─ 6
// └─ 7
Comonad是Monad對偶(Dual)的類別,在Haskell中,Comonad類別必須具備extract、duplicate和extend三個函數,在fp-ts中Tree和Store實作了這三個函數。
extract和of是對偶函數,of是將值封裝於型別容器中,extract則反過來將值從型別容器中取出,extract的HM型別簽名如下,其中w是Comonad類別的型別容器:
extract :: w a -> a // 將值從型別容器中取出
duplicate是flatten的對偶函數,它的HM型別簽名如下:
duplicate :: w a -> w (w a) // 將一個型別容器嵌套變成雙重型別容器嵌套
extend則是flatMap(chain)的對偶函數,它的HM型別簽名如下:
extend :: (w a -> b) -> w a -> w b
我們可以比較flatMap的HM型別簽名,其中m是Monad類別的型別建構子,
flatMap :: (a -> m b) -> m a -> m b
flatMap要轉換的函數是輸入為一般型別,輸出為Monad類別建構的型別;而Comonad則相反,它的輸入型別是Comonad類別建構的型別,輸出為一般型別。
接下來我們看看extend的用法,先建立isLeaf、size、sizeOfLeaves和depth四個函數。
// 判斷一棵樹是否為葉子
type IsLeaf = (t: Tree<any>) => boolean;
const isLeaf = (tree: Tree<any>) => tree.forest.length === 0;
// 計算樹所有的節點數
type Size = (t: Tree<any>) => number;
const size = reduce(0, (acc, _) => acc + 1);
// 計算樹結構中葉子的數量
type SizeOfLeaves = (t: Tree<any>) => number;
const sizeOfLeaves = <A>(tree: Tree<A>): number =>
(isLeaf(tree) ? 1 : 0) +
tree.forest.reduce((acc, child) => acc + sizeOfLeaves(child), 0);
// 計算樹的深度
type Depth = (t: Tree<any>) => number;
const depth = <A>(tree: Tree<A>): number =>
tree.forest.length === 0 ? 1 : 1 + Math.max(...tree.forest.map(depth));
console.log(extend(isLeaf)(numbersTree2)); // 一棵記錄numbersTree2每個子樹節點是否為葉子的樹
console.log(extend(size)(numbersTree2)); // 一棵記錄numbersTree2每個子樹節點的總節點數
console.log(extend(sizeOfLeaves)(numbersTree2)); // 一棵記錄numbersTree2每個子樹節點的總葉子數
console.log(extend(depth)(numbersTree2)); // 一棵記錄numbersTree2每個子樹節點的深度
這四個函數的輸入都是由Tree建構的型別,符合extend的函數的第一個參數要求,轉換後的函數的輸出入都是由Tree建構的型別,而且樹的結構完全一樣。
樹是應用非常廣泛的資料結構,在檔案系統、組織圖及HTML結構都可以看見它的身影。今天介紹了fp-ts/Tree模組中一些常用的函數,包含Monad介面中的map,ap和flatMap。由於Tree是多值的型別容器,Foldable類別中的reduce,reduceRight和foldMap也就相對重要,Tree的結構比Array複雜,這幾個函數的使用情形也比Array變化多。
Comonad的使用機會比較少,若有機會再介紹另一個Comnad類別的型別容器Store,今天分享的內容就到這邊,明天再見。
