
在上一篇文章中,我們介紹了 const toSlug = pipe(trim, toLowerCase, replaceSpaces, removeExclamation); 這種 Point-Free 風格。它雖然優雅,但也像個黑盒子:如果不看 pipe、trim、toLowerCase 的原始實作,我們要怎麼相信資料能順利「流」過這條函數鏈?
這正是大型 JavaScript 專案常見的困難。因為 JavaScript 是動態型別語言,函數的「契約」——輸入與輸出型別——往往是隱性的,只存在於命名、程式碼細節或開發者的腦海裡,導致協作與維護容易出錯。
為了解決這個問題,我們需要一種簡潔的通用語言。在函數式程式設計中,這種「世界語」就是型別簽章 (Type Signature),它源自 Hindley–Milner (HM) 型別系統,是 Haskell、ML、Scala、Elm 等函數式語言社群的共同語彙,今天我們就要來看看它是什麼~
作為一種動態型別語言,JavaScript 允許我們在不宣告型別的情況下定義變數與函數。這種彈性讓我們可以快速開發,但隨著應用程式複雜度增加,也帶來了挑戰。
假設我們需要一個工具函數來處理準備要送出的 API 資料,程式如下:
// 一個用來準備 API payload 的工具函數
// 我們必須閱讀程式碼才能知道它到底做了什麼。
// - `data` 的形狀是什麼?一個物件?一個陣列?
// - `config` 裡面有哪些 key?它們都是可選的嗎?
// - 回傳值的樣貌是什麼?有可能是 null 嗎?
function preparePayload(data, config) {
const payload = {...data };
if (config.includeTimestamp) {
payload.timestamp = Date.now();
}
if (config.formatter) {
return config.formatter(payload);
}
return payload;
}
要正確且安全地使用 preparePayload 這個函數,開發者只能閱讀它的程式來理解它的型別。函數的簽章實際上散落在程式碼的邏輯判斷中。這模式會讓重構和維護變得困難,有可能不小心就破壞了原有邏輯。
函數簽章(Type Signature):指的是函數所接受的參數型別與回傳值的型別
提到 JavaScript 是動態型別語言,應該有些人會想到:
「既然 JavaScript 是動態型別,我們改用 TypeScript 就好了,為什麼還要學 HM 型別簽章?」
關鍵在於:兩者雖然都能描述函數,但解決的問題層次不同。
const arr = [1, "a"]; TypeScript 可能會推論它是 (string | number)[]。這沒問題,但其實還有更「廣」的型別描述(例如 any[]),或更「窄」的描述(例如 [number, string])。在 Hindley–Milner 型別簽章的系統裡,這種情況會有一個唯一的、最通用的型別來描述;而在 TypeScript 裡,編譯器只會依照語境挑一個「合理」的型別,而不是保證全域最通用。另外,TypeScript 並非設計為「完全健全」的型別系統,它的官方設計目標的「Non-goals」就有說:「Apply a sound or "provably correct" type system. Instead, strike a balance between correctness and productivity.」,代表他們「不追求健全」的型別系統,而是追求正確性與生產力的平衡。
map :: (a -> b) -> [a] -> [b],但在 TypeScript 中則需寫成:const map = <A, B>(fn: (x: A) => B, arr: A[]): B[]
換句話說:
因此學習 HM 型別簽章的價值,不在於它取代 TypeScript,而在於它幫助我們以更純粹的語言來思考函數的本質。
為了感受型別簽章帶來的改變,我們來看一個在函數式程式設計中很常見的高階函數範例。
假設我們需要一個函數,可以根據指定的屬性名稱,將一個物件陣列分組。在沒有型別簽章的情況下,我們可能會寫出這樣的程式碼:
// 將物件陣列按照指定的屬性進行分組
const groupBy = (key, list) => {
return list.reduce((acc, obj) => {
const group = obj[key];
acc[group] = acc[group] || [];
acc[group].push(obj);
return acc;
}, {});
};
const users = [
{ id: 1, name: 'Alice', role: 'admin' },
{ id: 2, name: 'Bob', role: 'user' },
{ id: 3, name: 'Charlie', role: 'user' },
{ id: 4, name: 'David', role: 'guest' },
{ id: 5, name: 'Eve', role: 'admin' }
];
console.log(groupBy('role', users)); // groupBy 的回傳值是什麼結構?我們必須執行它或仔細閱讀程式碼才能確定。
/*
{
admin: [
{ id: 1, name: 'Alice', role: 'admin' },
{ id: 5, name: 'Eve', role: 'admin' }
],
user: [
{ id: 2, name: 'Bob', role: 'user' },
{ id: 3, name: 'Charlie', role: 'user' }
],
guest: [
{ id: 4, name: 'David', role: 'guest' }
]
}
*/
要理解這個 groupBy 函數,我們必須在腦中逐步執行 reduce 的邏輯:它接收一個字串 key 和一個物件陣列 list,然後回傳一個新的物件。這個新物件的鍵 (key) 是從原物件中取出的屬性值,而值 (value) 則是包含原始物件的陣列。整個過程需要花費心力去解讀與推斷。
現在,讓我們為這個函數加上一行 Hindley–Milner 風格的型別簽章註解:
// groupBy :: String -> [a] -> { String: [a] }
const groupBy = (key, list) => {
//... 相同的實作...
};
透過這行註解,groupBy 就變清晰了。這個簽章告訴我們:
String(用來分組的鍵)。[a](一個由任何型別 a 的元素組成的陣列)。{ String: [a] }(一個物件,其鍵為 String,其值為與輸入陣列相同型別 a 的元素組成的陣列)。模糊地帶消失了,我們不再需要閱讀實作細節,就能理解這個函數的行為。
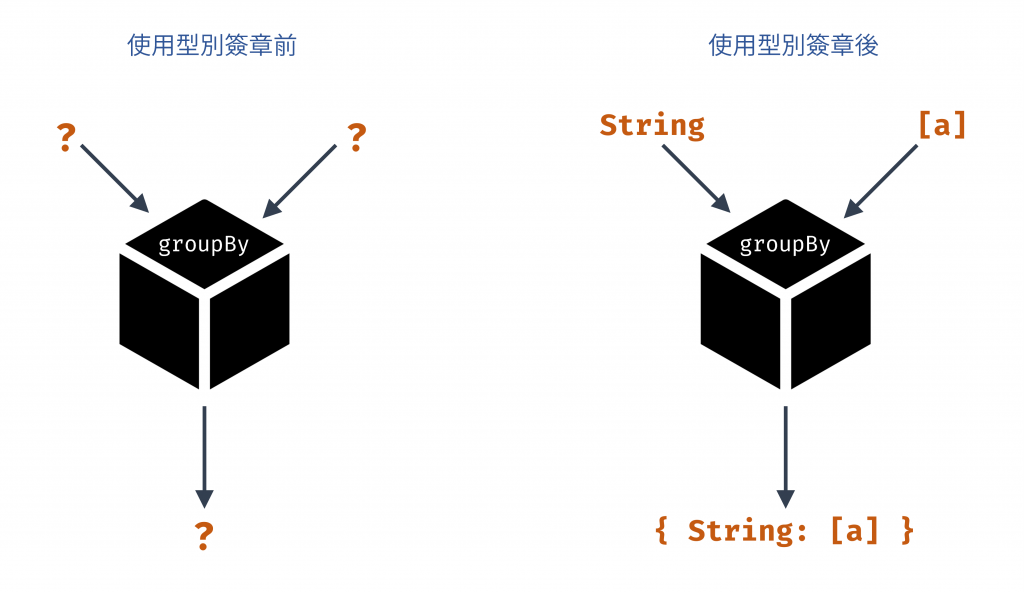
圖 1 使用型別參數前後的示意圖(資料來源: 自行繪製)
參考上圖,我們可以看到前後對比,左邊是使用型別參數前,groupBy 的輸入和輸出都未知,右邊的 groupBy 同樣是黑盒子,但我們可以知道輸入是 String 和 [a],輸出是 { String: [a] }。
接下來讓我們深入探討型別簽章,並說明其語法。
Hindley-Milner 風格的簽章就像一套精簡的語法,現在來逐一拆解它的組成。
:::是類型標註符號(type annotation symbol),類似「類型聲明運算子」,可將名稱與類型建立關聯。簡單來說,可以讀作「...的型別是」(has type of)。它將函數名稱與其型別定義分開。例如 head :: 就表示「head 函數的型別是...」。
:: 有點類似 TypeScript 的 :,例如在 TypeScript 中我們會寫 let age: number = 25; 來聲明 age 是 number 型別,在 Hindley-Milner 型別簽章中就會用 head :: 來表示 head 函數的型別->:這是最重要的分隔符。它分隔了參數與回傳值。一個簡單的規則是 「最後一個箭頭右邊的,永遠是最終的回傳值型別」 。例如 a -> b -> c 代表這個函數最終會回傳一個型別為 c 的值。先從最簡單的具體型別開始看:
// parseInt :: String -> Number
// toUpperCase :: String -> String
第一行表示 parseInt 是一個接收 String 並回傳 Number 的函數。第二行表示 toUpperCase 接收 String 並回傳 String。非常直觀 👍
以下再用一個表格來分別說明 capitalize :: String -> String 各部分對應的意義。
| 部分 | 代表的意義 | 對應概念 |
|---|---|---|
capitalize |
函式名稱,表示要執行的操作,例如將字串首字母轉大寫 | 函式(Function) |
:: |
類型標註(type annotation),表示 capitalize 的類型 |
類型標註符號(Type Annotation Symbol) |
String |
函式的輸入類型,表示 capitalize 接受一個字串 |
參數類型(Input Type) |
-> |
函式映射關係,表示函式從一個類型轉換到另一個類型 | 函式類型箭頭(Function Arrow) |
String |
函式的輸出類型,表示 capitalize 回傳一個字串 |
回傳類型(Output Type) |
根據上述,capitalize :: String -> String 就是表示 capitalize 這函數接受一個 String 參數,並且會回傳 String。
HM 型別系統的想法最早出現在 1969 年,當時數學家 J. Roger Hindley 在研究「組合子邏輯」時,提出了「最一般型別 (principal type)」的概念。簡單來說,就是如果一段程式能被加上型別,那一定存在一個「最通用」的型別方案,其他的型別都可以從它推導出來。
幾年後的 1978 年,電腦科學家 Robin Milner 在設計 ML 語言(早期一種的函數式語言)時,重新發明並應用了這想法。他的目標很是讓程式同時「安全」又「好寫」。程式設計師不用到處寫型別註解,編譯器就能自動幫你推算出正確的型別,還能在編譯時期就避免型別錯誤。
到了 1982 年,Luis Damas 與 Milner 一起把這整套系統嚴謹地整理成理論基礎,這才有了後來完整的 Hindley–Milner 型別系統(有時也叫 Damas–Milner 系統)。它成為 Haskell、OCaml、F# 等函數式語言背後的重要基礎。
HM 系統誕生的原因就是為了解決一個痛點:怎麼讓我們同時擁有靜態型別的安全性,又不用寫一大堆型別註解? 答案就是靠強大的型別推論 (type inference),讓編譯器自動幫你找出「最一般型別」。
a 與 b 的魔力在程式設計中,「多型」(Polymorphism) 的核心思想是讓一個介面或符號能適用於不同型別的實體,簡單來說,就是讓一份程式碼能處理多種資料型別。在函數式程式設計中,我們最關心的是「參數化多型 (Parametric Polymorphism)」。參數化多型的核心思想在於,函數或資料結構的撰寫方式是通用的,它能以完全一致的邏輯來處理各種型別,而不需依賴它們的具體內容。一個參數化多型的函數,其行為對於它所操作的所有型別都是統一的 。
在 HM 簽章中,我們使用小寫字母(通常是 a, b, c...)作為型別變數 (type variables)。它們就像是型別的佔位符,代表「任何型別」。
補充:參數多型 (Parametric polymorphism)
參數多型在程式設計語言與類型論中是指聲明與定義函數、複合類型、變數時不指定其具體的類型,而把這部分類型作為參數使用,使得該定義對各種具體類型都適用。
a -> a// head :: [a] -> a
// 接收一個由「任何型別 a」組成的陣列,並回傳一個「相同型別 a」的元素。
const head = (arr) => arr[0];
head([1, 2, 3]); // a 是 Number,回傳 Number (1)
head(['x', 'y', 'z']); // a 是 String,回傳 String ('x')
這裡的關鍵是,a 在簽章中出現了兩次。這是一個約束:如果輸入的陣列是 [Number],那回傳值必須是 Number,不可能是 String 或 null。
a -> b當函數涉及到型別轉換時,我們會使用不同的型別變數。map 函數是最好的例子:
// map :: (a -> b) -> [a] -> [b]
// 1. 接收一個函數,這個函數能將型別 a 轉換為型別 b。
// 2. 接收一個由型別 a 組成的陣列。
// 3. 回傳一個由型別 b 組成的陣列。
const map = (fn, arr) => arr.map(fn);
const numbers = [1, 2, 3]; // a 是 Number
const double = (n) => n * 2; // double :: Number -> Number
const toString = (n) => String(n); // toString :: Number -> String
map(double, numbers); // 在此例中,a 和 b 都是 Number。回傳 [2, 4, 6]
map(toString, numbers); // 在此例中,a 是 Number,b 是 String。回傳 ['1', '2', '3']
map 的簽章詮釋了它的多功能性。a 和 b 可以是相同的型別,也可以是完全不同的型別。這個簽章本身就幾乎完整的說明了 map 的功能。
Currying(柯里化)是 FP 重要的元素之一,HM 簽章的語法設計和 Currying 天生契合,因為箭頭 -> 是向右結合的,這代表 a -> b -> c 在解析時會被視為 a -> (b -> c),也就是傳入 a 參數會獲得一個 b -> c 的函數,這剛好是 Currying 函數的本質。
// add :: Number -> Number -> Number
const add = a => b => a + b;
const add5 = add(5); // add(5) 的回傳值是什麼型別?
// 根據簽章 a -> (b -> c),5 對應第一個參數 a(Number),現在 add(5) 回傳的是 Number -> Number
add 的簽章告訴我們,它是一個接收 Number,並回傳一個「接收 Number 並回傳 Number 的新函數」的函數。剛好對應柯里化的實作。
再看一個更複雜的例子:
// replace :: RegExp -> String -> String -> String
const replace = pattern => replacement => str => str.replace(pattern, replacement);
這個簽章可以這樣解讀:replace 是一個接收 RegExp,回傳一個新函數(String -> String -> String);這個新函數接收 String(替換內容),再回傳另一個新函數(String -> String);這最後一個函數接收 String(原始字串),最終回傳 String。型別簽章完整地描述了整個柯里化的鏈條。
第一次接觸型別簽章時,很容易迷失,所以這裡又再列了一些範例來理解型別簽章~希望能多看多熟悉,因為後續介紹 FP 工具,都會用型別簽章來說明函數的輸入輸出。
// filter :: (a -> Bool) -> [a] -> [a]
// 接受 (a -> Bool) 函式與 a 陣列 [a],回傳符合條件的 a 陣列 [a]
const filter = curry((f, xs) => xs.filter(f));
// reduce :: ((b, a) -> b) -> b -> [a] -> b
// 第一個參數 ((b, a) -> b) 是一個函式,接受 b (累積值)和 a(當前值),回傳 b (新累積值)
// 第二個參數 b 是初始值
// 第三個參數 [a] 是 a 的陣列,對應要處理的陣列資料
// 最終結果是 b,reduce 在 a 陣列上進行累積運算,最後得到累進值 b
const reduce = curry((f, x, xs) => xs.reduce(f, x));
// match :: Regex -> String -> [String]
// 接受 Regex 和 String,回傳 String 陣列 [String]
const match = curry((reg, s) => s.match(reg));
// join :: String -> [String] -> String
// 接受一個 String 和一個 String 陣列 [String],回傳 String
const join = curry((what, xs) => xs.join(what));
雖然 TypeScript 和 HM 簽章代表的意義不同,但還是有些相似處,以下比較 HM 簽章與 TypeScript 的泛型語法,展示它們如何用不同的語法來表達相同的核心思想。
| 概念 | Hindley-Milner 標記法 | TypeScript 標記法 |
|---|---|---|
| 具體型別函式 (Simple Function) | isEven :: Number -> Boolean |
const isEven = (n: number): boolean => ...; |
| 單一泛型 (Generic, Same Type) | head :: [a] -> a |
const head = <T>(arr: T[]): T => ...; |
| 泛型轉換 (Generic, Transform) | map :: (a -> b) -> [a] -> [b] |
const map = <T, U>(fn: (x: T) => U, arr: T[]): U[] => ...; |
| 柯里化 (Currying) | add :: Number -> Number -> Number |
const add = (a: number) => (b: number): number => ...; |
| 高階函數 (Higher-Order Function) | applyTwice :: (a -> a) -> a -> a |
const applyTwice = <T>(fn: (x: T) => T, value: T): T => fn(fn(value)); |
上述表格中,我們可以觀察到,雖然兩者都能表達參數化多型,但對於函數式程式設計中常見的高階、柯里化函數,HM 的語法通常更簡潔、更容易閱讀。
在 Philip Wadler 的論文 《Theorems for Free!》 中,他指出:一個足夠多型的型別簽章,已經對函數的可能實作施加了強大的邏輯限制。因此,我們僅透過閱讀型別簽章,就能直接推導出一些「自由定理 (free theorems)」,這些定理描述了函數必然遵守的行為規律,而無需檢視或撰寫實際程式碼。
identity 的必然性// identity :: a -> a
我們可以做一些邏輯推導:
a 都有效。a 的參數。a 一無所知。它不知道 a 是否為 String 而擁有 .length 屬性,也不知道 a 是否為 Number 而可以進行加法運算。它沒有任何可以對 a 進行的特定操作。a 的值。a 都成立的合法實作,就是原封不動地回傳它所接收到的那個參數。結論:a -> a 這個型別本身就證明了任何實現它的函數必然是恆等函數 (identity function)。這就是我們免費得到的第一個定理,透過型別簽章理解了 identity 函數的實作,且不需看他的程式碼內容。
head 的來源保證現在來看另一個例子:
// head :: [a] -> a
一樣做一些邏輯推導:
a 的值。identity 一樣,函數對 a 一無所知,所以它無法創造一個 a。a 型別值的地方,就是從輸入的 [a] 陣列中取得。結論:這個簽章證明了 head 函數的回傳值必定來自於輸入陣列中的某個元素。它不可能回傳一個 hard code 的 42 或 null(除非 a 恰好就是 Number 或 Null 型別),因為那樣會違反它對「所有」型別 a 都有效的承諾。
free theorems 可為程式碼的重構提供數學面向的的保證。
讓我們思考一個型別為 f :: [a] -> [a] 的函數,例如 reverse 或 sort。根據我們之前的推導,這個函數因為對 a 一無所知,所以它能做的操作僅限於:重新排序元素、複製元素、或丟棄元素。它不可能改變元素自身的內容(例如把一個數字加一,或把一個字串轉為大寫),因為如果改變了,回傳值就是 [b] 而不是相同的 [a]。它對元素的值是「無知」的。
現在,我們將這個「無知」的函數 f 與我們熟悉的 map 函數組合起來。map 的作用恰恰相反,它的目的就是用一個轉換函數 g 來改變陣列中的每一個元素。
我們有兩種組合方式:(💡 提醒:compose 是由右到左執行)
compose(map(g), f):先用 f 重排陣列,然後用 map(g) 轉換每個元素。compose(f, map(g)):先用 map(g) 轉換每個元素,然後用 f 重排轉換後的陣列。因為 f 對元素的值是無知的,它根本不在乎自己操作的是原始的元素,還是被 g 轉換過的元素。它執行的重排、複製、丟棄邏輯都會是完全一樣的。這就導出了一個的 free theorems:
map(g). f = f. map(g)
(補充,. (點)這個符號代表函數組合 (function composition),f. g 的意思就是「先執行 g 函數,然後把 g 的結果作為輸入傳給 f 函數」。換句話說,(f. g)(x) 就等同於 f(g(x))。)
更白話理解這公式,意思就是 「先換顏色再洗牌」和「先洗牌再換顏色」結果是相同的。
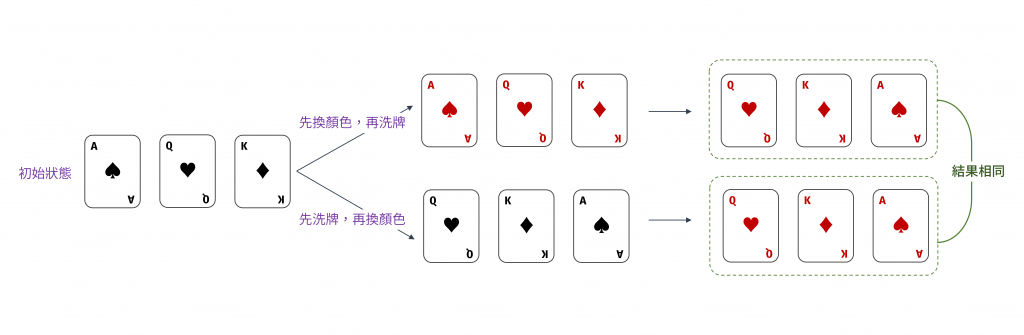
圖 2 「先換顏色再洗牌」和「先洗牌再換顏色」結果是相同的(資料來源: 自行繪製)
map(g). f = f. map(g) 不僅是一個學術上的等式,還是一條可以安全應用的程式重構規則。它證明了這兩種組合方式在結果上是完全等價的。以下用程式說明:
// reverse :: [a] -> [a]
const reverse = arr => [...arr].reverse();
// toUpperCase :: String -> String
const toUpperCase = str => str.toUpperCase();
// map :: (a -> b) -> [a] -> [b]
const map = (fn, arr) => arr.map(fn);
const list = ['a', 'b', 'c'];
// 路徑 1: 先 reverse,再 map
// map(toUpperCase, reverse(list))
// -> map(toUpperCase, ['c', 'b', 'a'])
// -> ['C', 'B', 'A']
// 路徑 2: 先 map,再 reverse
// reverse(map(toUpperCase, list))
// -> reverse(['A', 'B', 'C'])
// -> ['C', 'B', 'A']
// 結果完全相同。型別簽章已預言了這一切!
console.log(map(toUpperCase, reverse(list))); // ['C', 'B', 'A']
console.log(reverse(map(toUpperCase, list))); // ['C', 'B', 'A']
另外也用下圖說明型別簽章對函數的約束力,即使我們不知道函數內部實作,也能確定輸入輸出的樣貌,不會有非預期的值(例如 🍌)出現。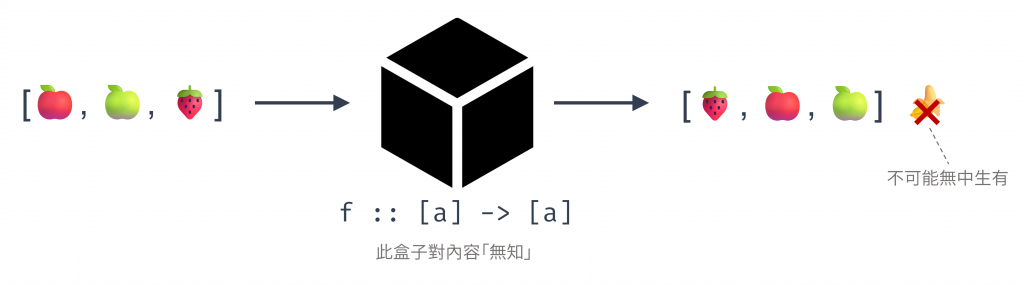
圖 3 型別簽章約束函數的行為,衍伸出 free theorems(資料來源: 自行繪製)
free theorems 展示的「型別約束行為」的原則,促使了一種應用:用型別簽章來搜尋函數。
Haskell 有一個名為 Hoogle 的 API 搜尋引擎,它讓開發者能透過型別簽章來尋找需要的函數。
假設某天你忘記了「檢查一個元素是否存在於陣列中」的函數叫什麼名字。但你知道它的「形狀」:它應該接收一個元素(型別為 a),一個該元素的陣列(型別為 [a]),然後回傳一個布林值(Bool)。所以,它的型別簽章應該是 a -> [a] -> Bool。
我們可以用 a -> [a] -> Bool 在 Hoogle 中直接搜尋這個型別簽章,它會回傳所有符合或近似符合這個簽章的函數列表,如下圖:
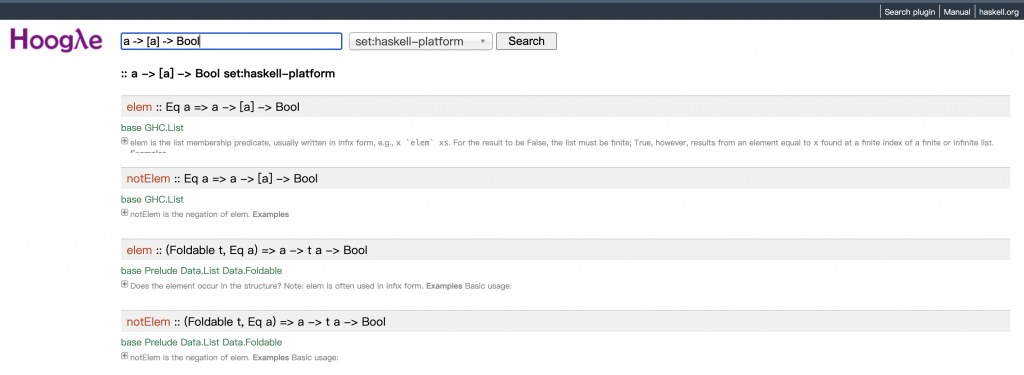
圖 4 Hoogle 截圖示意
在這種情況下,elem 函數(等同於 JavaScript 的 includes)就是搜尋結果之一 。
能實現這功能的原因就是參數化多型。a -> [a] -> Bool 的簽章限制了函數的可能行為,使型別本身成為一個有用的搜尋關鍵字。
在前端開發中,我們不能直接用 Haskell,但可以用 fp-ts 這樣的函式庫來理解 FP。fp-ts 參考 Haskell/Scala 的抽象(Functor/Applicative/Monad…),並用型別編碼實作 Higher-Kinded Types(HKTs)的效果,以在 TS 中擁抱「以型別驅動的抽象」。因此我們可以在 TS 中使用熟悉的 Haskell 風格型別類(Option/Either/Task…),以簽章先行治理副作用與錯誤處理。
以上 Functor/Applicative/Monad 或是 Higher-Kinded Types 這些名詞不懂沒關係,簡單來說 fp-ts 用 TypeScript 實作了許多工具來模擬 Haskell 這種專門 FP 的語言,因此參考 fp-ts 可以讓我們更接近、更了解 FP 的世界。
用三個問題總結今天的文章。
為了對抗動態型別 JavaScript 的模糊性。它們是明確的契約,能改善團隊溝通、降低認知負擔,並迫使我們在函數式程式設計這個高度抽象的世界中,帶著清晰的意圖去設計函數。
這是一個從「實作優先」(閱讀程式碼來猜測意圖)到「契約優先」(閱讀簽章來理解行為)的轉變。
它是一種源自 FP 世界的、簡潔而強大的標記法,用以描述函數的介面。它不僅僅是文件,其對參數化多型 (a -> b) 的支持,更提供了 free theorems——關於函數行為的邏輯保證,讓我們能進行更安全的推理與重構。它是一種輔助思考的工具。
