引言

大家可能會跟我有一樣的經驗，就是每天出門前都會糾結一個問題：「今天要不要帶傘？」
帶傘的話，包包變好重；不帶的話，下雨就慘了...（但是身為政大的學生，包包裡一定要放一把傘才是明智的選擇🥺）

決定「要不要帶傘」，基本上不外乎就是幾個判斷標準，你可能會根據這一週以來的天氣來做判斷：

• 如果前幾天都下雨，今天又是陰天，你可能會認為「今天很可能也會下雨」，所以帶傘。
• 如果前幾天都是晴天，今天又是大太陽，你就可能覺得不用帶傘。

Naive Bayes 做的判斷也很像這個模式。它會根據 「過去的觀察」 計算每個特徵出現的機率，然後再推算某事件發生的機率。

在天氣的比喻裡，我們觀察的是「天氣現象」，要推斷的事件是「是否會下雨」。
在文本分類裡，Naive Bayes 觀察的就是特徵，推斷的結果可能就會是「好評或負評」。

接下來我們就來更詳細的了解 Naive Bayes 背後的運算方式，還有做簡單的程式實作！

Naive Bayes Classifier

Naive Bayes Classifier 是一種經典的機率分類模型，常用於文本分類的任務。主要有兩個核心概念：

1. 條件獨立假設

Naive Bayes 之所以 naive，是因為它「天真」地假設每個條件彼此獨立，也就是說它認為每個特徵對分類結果的影響互不干擾。

舉例來說，我們要判斷今天看電影要不要配飲料。而我們有兩個資訊：電影類型以及電影長度。
條件獨立假設就是說：「電影類型對喝飲料的影響，不會受到電影長度的影響；電影長度的影響，也不受類型影響。」

雖然現實中這兩個因素應該會交互影響，短的喜劇可能會讓人比較想配零食跟飲料，長的恐怖片可能讓人不太想喝飲料（怕嚇到尿褲子）。但是當我們假設條件獨立的話，可以讓整個計算簡單一些～

2. 貝氏定理（Bayes’ Theorem）

貝氏定理的概念是 「利用已知的條件來反推未知的機率」 。

像是要不要帶傘出門的例子，我們想知道「今天會下雨的機率」，而目前已知的資訊有：

• 今天早上看到天空陰陰的
• 過去一週的經驗：陰天的日子有幾天真的下雨

貝氏定理就是把這些資訊組合起來計算：

1. 先看「過去下雨的頻率」→ 先驗機率 P(A)
2. 再看「下雨時陰天的頻率」→ 條件機率 P(B|A)
3. 合併計算 → 得到「今天為陰天的情況下，下雨的機率」→ 後驗機率 P(A|B)

就像我們在用「已知的線索」來推斷「未知的結果」的過程，Naive Bayes 就是把這個方法用在文本分類。每個詞都是一個「線索」，而要推斷的就是「文本分類的結果」。

程式實作

1. 資料準備

我們使用的資料是從 kaggle 取得的 IMDb 50K Cleaned Movie Reviews

import kagglehub
import os

# Download latest version
path = kagglehub.dataset_download("ibrahimqasimi/imdb-50k-cleaned-movie-reviews")

print("Path to dataset files:", path)
print(os.listdir(path))

# === Output ===
Path to dataset files: /root/.cache/kagglehub/datasets/ibrahimqasimi/imdb-50k-cleaned-movie-reviews/versions/1
['IMDB_cleaned.csv']

import pandas as pd

csv_path = os.path.join(path, "IMDB_cleaned.csv")  
df = pd.read_csv(csv_path)
print(df.info())

# === Ouput ===
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 5000 entries, 0 to 4999
Data columns (total 3 columns):
 #   Column          Non-Null Count  Dtype 
---  ------          --------------  ----- 
 0   review          5000 non-null   object
 1   cleaned_review  5000 non-null   object
 2   sentiment       5000 non-null   object
dtypes: object(3)
memory usage: 117.3+ KB
None

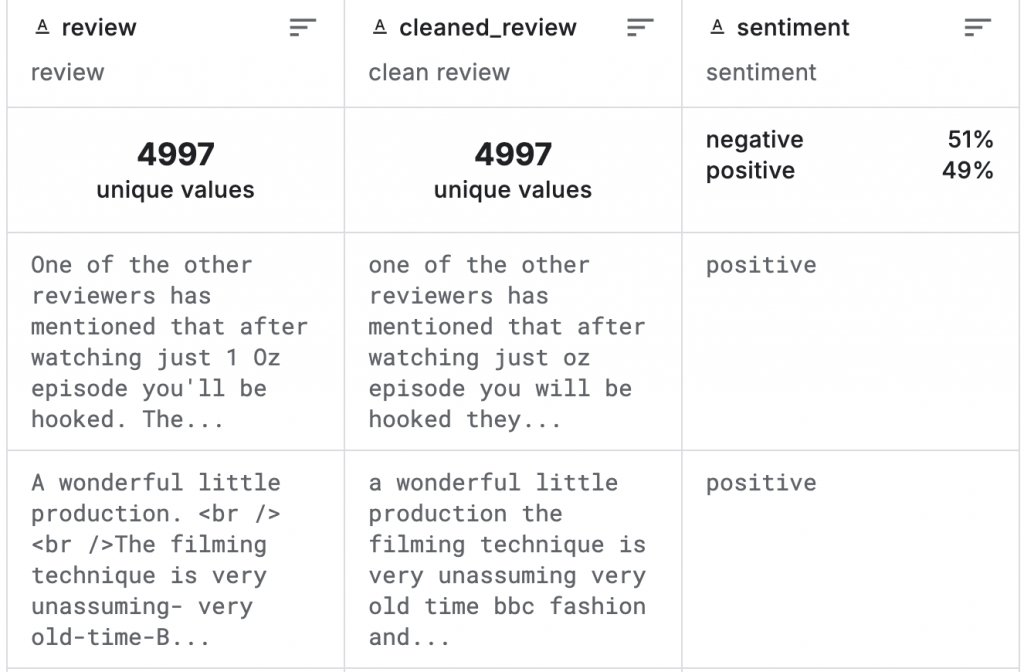
資料集共有 5000 筆資料，三個欄位：

• review：原始的評論
• cleaned review：清理過後的評論
• sentiment：情緒標記（positive & negative）

2. 資料劃分

• X 是訓練資料
• y 是正確答案
• 訓練集跟測試集切分為 8:2

from sklearn.model_selection import train_test_split

X = df["cleaned_review"]
y = df["sentiment"]

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

3. 特徵轉換

將訓練資料 (X) 轉換為 TF-IDF 向量

from sklearn.feature_extraction.text import TfidfVectorizer

vectorizer = TfidfVectorizer(stop_words="english", max_features=5000)
X_train_vec = vectorizer.fit_transform(X_train)
X_test_vec = vectorizer.transform(X_test)

4. 訓練 Naive Bayes 分類器

• 用訓練集訓練
• 用測試集預測

from sklearn.naive_bayes import MultinomialNB

# 訓練
NB_model = MultinomialNB()
NB_model.fit(X_train_vec, y_train)

# 預測
y_pred = NB_model.predict(X_test_vec)

5. 評估表現

from sklearn.metrics import (
    accuracy_score,
    precision_score,
    recall_score,
    f1_score,
    classification_report
)

# Accuracy
print("Accuracy:", f"{accuracy_score(y_test, y_pred):.3f}")

# Precision, Recall, F1
print("Precision:", f"{precision_score(y_test, y_pred, pos_label='positive'):.3f}")
print("Recall:", f"{recall_score(y_test, y_pred, pos_label='positive'):.3f}")
print("F1 Score:", f"{f1_score(y_test, y_pred, pos_label='positive'):.3f}")

# 詳細分類報告
print("\n分類報告:\n", classification_report(y_test, y_pred))

# === Output ===
Accuracy: 0.828
Precision: 0.825
Recall: 0.804
F1 Score: 0.815

分類報告:
               precision    recall  f1-score   support

    negative       0.83      0.85      0.84       530
    positive       0.83      0.80      0.81       470

    accuracy                           0.83      1000
   macro avg       0.83      0.83      0.83      1000
weighted avg       0.83      0.83      0.83      1000

6. 畫出混淆矩陣

from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns

cm = confusion_matrix(y_test, y_pred, labels=["positive", "negative"])
plt.figure(figsize=(6, 4))
sns.heatmap(cm, annot=True, fmt="d", cmap="Blues",
            xticklabels=["positive", "negative"],
            yticklabels=["positive", "negative"])

plt.xlabel("Predicted")
plt.ylabel("Actual")
plt.title("Confusion Matrix - Naive Bayes")
plt.show()

結語

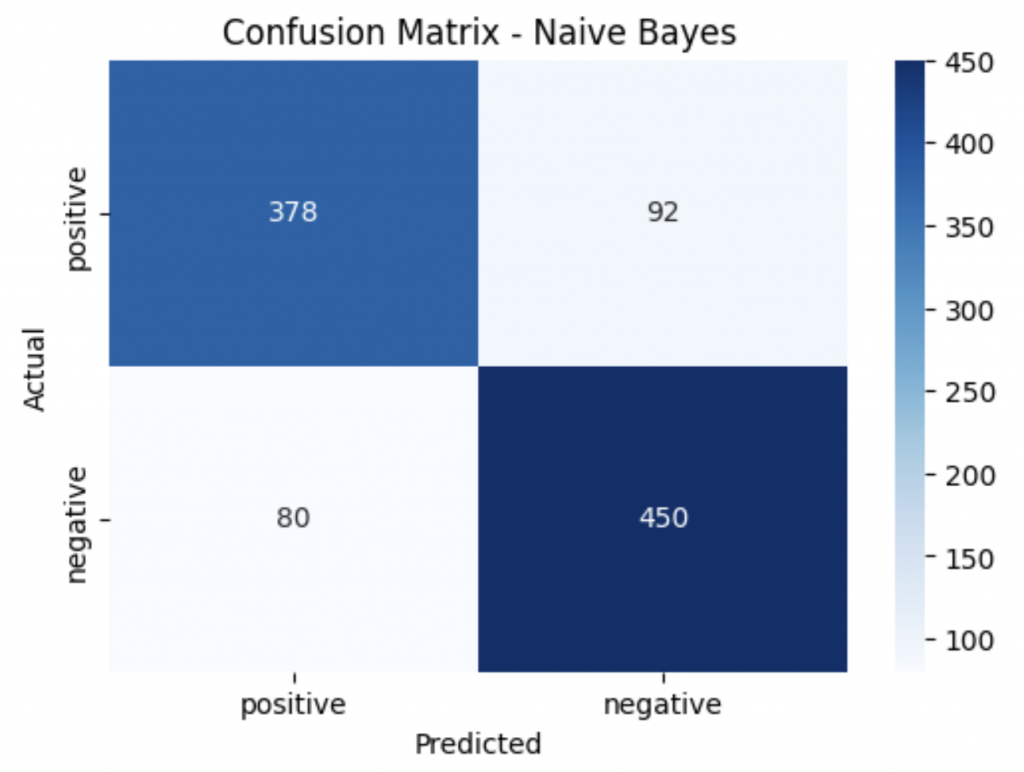
Naive Bayes 雖然是個相對簡單的模型，但這樣子的機率思維在分類任務上還是可以有一定程度的表現。
明天我們會介紹另一種分類算法 「Tree-based 模型」 🌳。讓我們來看看模型是如何做「選擇」吧～～

References

• 貝氏分類器(Naive Bayes Classifier)(含python實作)
• [機器學習首部曲] 貝氏分類器 Bayesian Classifier