
在上一篇初探容器的文章中,留下了一個問題:當面對一組值時,要如何找到一種通用的模式,能可靠地將它們組合為一?
在解答問題之前,先來看看一個更普遍的觀念——組合 (Composition)。之後會介紹的 Functor、Monad、Applicative 等工具,核心都在回答同一個問題:如何在程式中安全且可靠地進行組合。而 Monoid 正是這些組合抽象的基礎。理解 Monoid,能幫助我們更好地看懂 Functional Programming 工具的設計哲學。
舉幾個日常任務來說:加總一個數字陣列、串接一個字串陣列、或合併一系列設定物件。乍看之下,它們毫不相干,但其實背後共享同一種簡單卻強大的結構。在 FP 的世界裡,這個結構有個名字——Monoid。
事實上,我們幾乎每天都在使用 Monoid,只是沒有意識到而已。雖然「Monoid」這個詞聽起來帶點數學的味道(它源自抽象代數與範疇論),但它的本質比名稱要直觀得多。今天就來看看 Monoid 的定義與規則,並理解為什麼它能成為 FP 世界中「組合」的基礎。
Monoid 的世界由一個「集合」和一個作用於其上的「二元操作」所構成。
首先,Monoid 的所有活動都發生在一個「集合」(Set)之上,在程式設計的世界裡,我們可以將相同型別的值視為一個集合,簡單回顧一下集合的定義:
集合是一種把若干個元素放在一起的方式,不考慮元素的順序和重複性。集合可以用大括號
{}來表示,例如{ 2, 4, 6 }是一個集合,包含了三個元素 2, 4 和 6。集合可以用來描述任何事物的分類或歸納。
我們可以用集合來思考程式設計中的型別,將「同型別的可取值域」來對應集合,例如:
{0, 1, 2 ... Max_Number}(假設 Number 都是正整數){'a', 'b', 'c', ...}
{true, false}
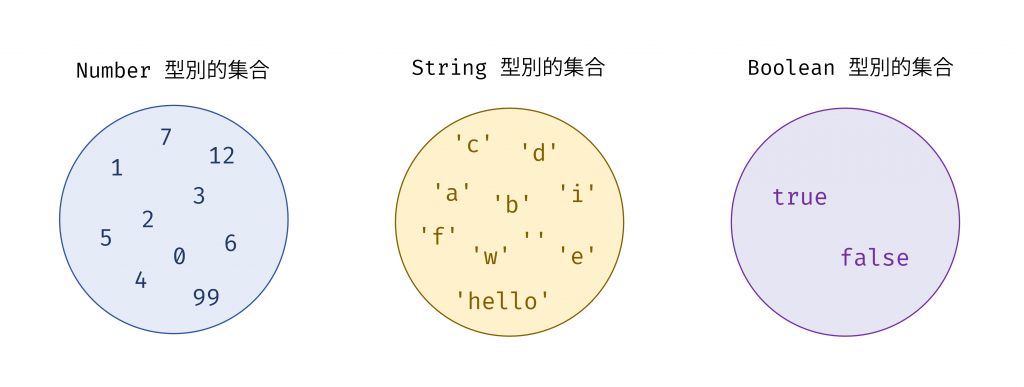
圖 1 同一型別代表一個集合(資料來源: 自行繪製)
這個「單一型別」的約束是 Monoid 世界的基礎,它確保接下來要介紹的操作能夠一致且可預測地進行。
更多集合與型別的說明可參考 用集合思考型別、Day02. 「型別」請「集合」 - Type is Set。
補充:本文的例子以 JavaScript 情境為主;理論上,請先選定集合 M,再定義其上的二元操作 • 與單位元素 e。
有了值的集合,我們還需要一種方法來與讓集合內的值彼此互動。這個方法就是「二元操作」(Binary Operation)。它是一個簡單的規則或函式,專門接收來自同一個集合的兩個元素,並將它們組合成第三個元素。
舉例來說:
+ 就是一個二元操作。它接收兩個數字,回傳一個新的數字,例如 3 + 4 會得到新數字 7
+ 或 .concat() 方法就是一個二元操作,例如 "Good" + " Morning" 會得到 "Good Morning"
.concat() 方法也是一個二元操作,例如 [1, 2].concat([3, 4]) 會得到 [1, 2, 3, 4]
這個操作是 Monoid 的「動詞」,它定義了集合內的元素如何組合彼此。
而這個「二元操作」還需要滿足三個規則,分別介紹如下。
第一條規則是封閉性(Closure),封閉性的定義非常簡單:對於我們集合 M 中的任意兩個元素 a 和 b,執行二元操作 a • b 的結果,必須仍然是集合 M 內的元素。
(可以把 • 符號想成組合兩個元素的操作)
可以透過一個「混合顏料」的例子來理解。想像你的調色盤就是一個顏色的集合。當你從調色盤上選取兩種顏色(例如紅色和黃色)並將它們混合,你得到的新顏色(橘色)仍然是一種顏色,可以被放回調色盤上。你不會因為混合了兩種顏色而突然得到一個聲音、一個數字或任何不屬於「顏色」這個集合的東西。這就是封閉性。
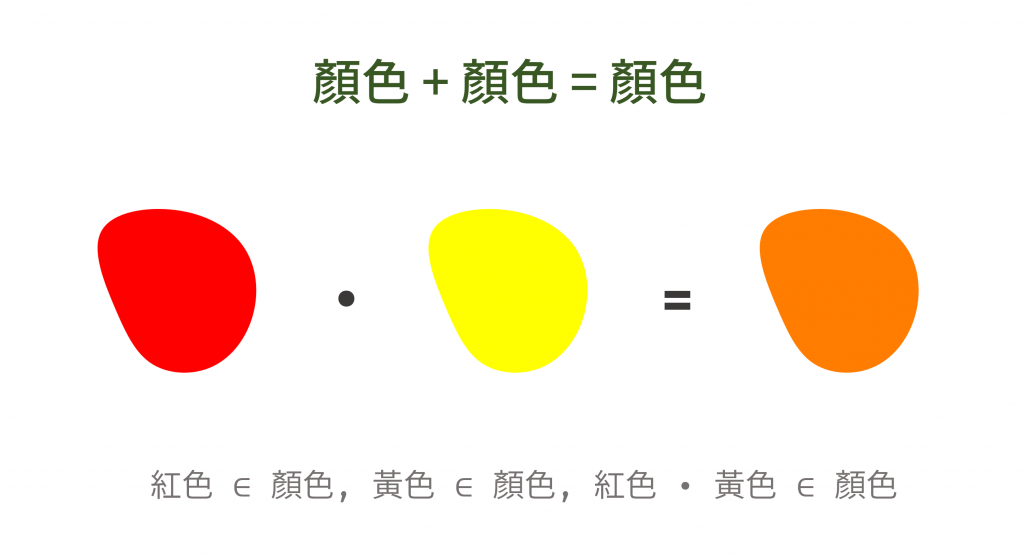
圖 2 顏色組合顏色後,仍然會得到一個顏色(資料來源: 自行繪製)
在程式語言的世界中(以 JavaScript 為例),這個特性無處不在:
5 + 3 的結果是 8。5、3 和 8 全都是 Number 集合的成員。因此,數字的加法具有封閉性"hello" + " world" 的結果是 "hello world"。"hello"、" world" 和結果 "hello world" 都是 String。因此,字串串接也具有封閉性當一個操作具備封閉性時,它就提供了一種可預測性的保證。我們無需檢查 number + number 的回傳值,因為我們確信它永遠會是一個 number。這種確定性消除了整整一大類的潛在型別錯誤。
更重要的是,由於操作的輸出型別與輸入型別完全相同,這代表運算的結果可以立即被用作下一次相同操作的輸入。這就是實現鏈式操作的關鍵所在,例如 (a • b) • c • d... 。如果沒有封閉性,這個鏈條在第一步之後就會斷裂,因為 (a • b) 的結果可能是一種 c 無法處理的新型別。
結合律(Associativity)的定義是:對於任意三個元素 a、b 和 c,(a • b) • c 的運算結果永遠等於 a • (b • c) 。這代表在一個連續的操作序列中,只要元素的順序不變,我們如何為二元操作的順序分組(也就是括號的位置)並不會影響最終的結果。
來看兩個簡單的例子:
(2 + 3) + 4 的結果是 5 + 4 = 9,這與 2 + (3 + 4) 的結果 2 + 7 = 9 完全相同("a" + "b") + "c" 的結果是 "abc",這與 "a" + ("b" + "c") 的結果也完全相同結合律的意義遠不止於數學上的優雅。在計算機科學中,它是實現高效能與可擴展性計算的關鍵。它讓我們能將一個龐大的計算任務分解為多個獨立小任務來執行。
假設我們要對一個包含一百萬個數字的陣列進行求和:1 + 2 + 3 +... + 1,000,000。如果嚴格按照從左到右的順序進行,這將是一個漫長的循序處理過程。然而,由於加法滿足結合律,我們可以將這個任務「分而治之」(Divide and Conquer)。例如,我們可以讓一個 CPU 核心計算前半部分 (1 +... + 500,000) 的和,同時讓另一個 CPU 核心計算後半部分 (500,001 +... + 1,000,000) 的和 。最後只需將這兩個中間結果相加,就能得到最終的總和。
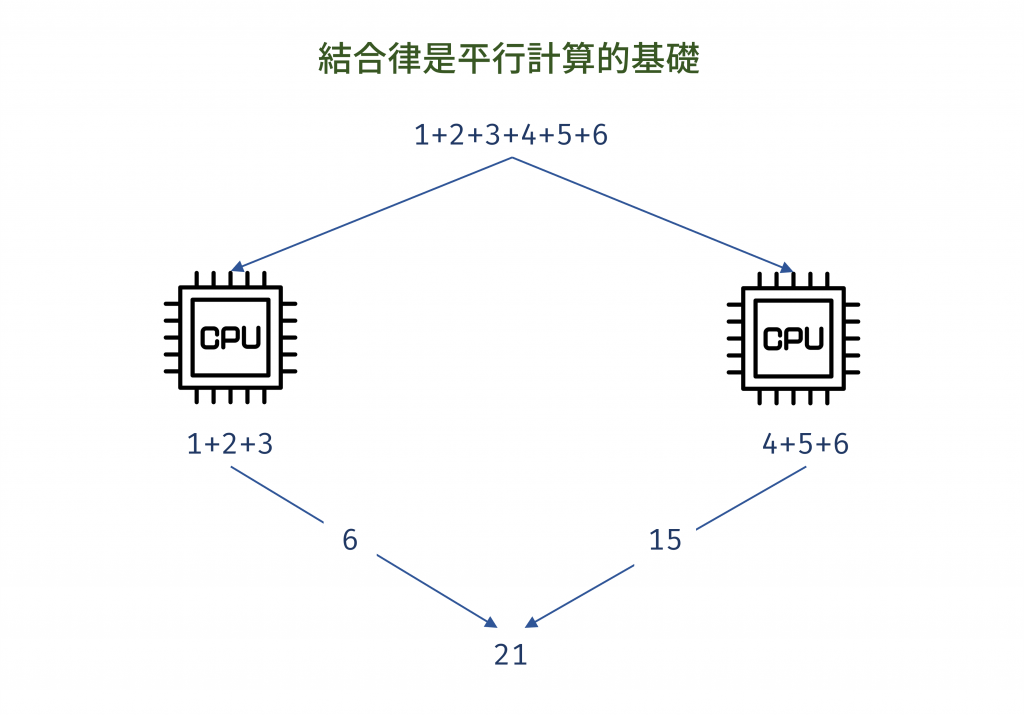
圖 3 結合律是平行計算的基礎(資料來源: 自行繪製)
這裡只是簡單以加法來舉例,可以把加法替換成其他複雜運算任務,當我們要執行一個複雜運算時,在單一電腦上計算會耗時很久,但如果可以分別在兩個電腦各運算一部分,兩個電腦可以平行、同時運算,最後再整合起來,這樣就能更省時間,而能夠「分別且平行的運算」的前提,就是這運算需滿足結合律。
我們改變了運算的分組方式,但結合律保證了最終結果的正確性。這種策略是平行處理、分散式計算(例如 MapReduce 框架)甚至是增量計算的理論基礎。因此,結合律是數學上的一項保證,而程式設計的世界參考了這個保證,讓我們能優化效能,同時產出正確的結果。
除了平行處理,結合律還帶來了另一個強大的好處:漸進式累積 (incremental accumulation)。
想像一個需要即時更新的場景,例如一個顯示當日總銷售額的電商後台儀表板。
這個看似理所當然的操作,其背後的數學保證正是結合律。它確保了 (前 99 筆訂單總和) + 第 100 筆訂單金額 的結果,與從頭加總 訂單 1 + 訂單 2 +... + 訂單 100 的結果是完全一樣的。
這種模式對於處理串流資料 (streaming data)、事件紀錄 (event logging) 或任何需要隨時間更新狀態的系統至關重要。我們不需要在每次更新時都重新計算整個歷史紀錄,只需將舊的結果與新的資料組合即可,這大大提升了系統的效率和即時性。
Monoid 的最後一條法則是必須存在一個特殊的「單位元素」(Identity Element),我們通常用 e 來表示。這個元素的神奇之處在於,當它與集合中的任何元素 a 進行組合時,完全不會改變 a 的值。也就是說,a • e = a 且 e • a = a 。它就像是特定操作下的「空氣」,一個「什麼都不做」的值。
每個 Monoid 都有其專屬的單位元素:
+),單位元素是 0,因為任何數字加上 0 都等於它本身(例如 5 + 0 = 5)*),單位元素是 1,因為任何數字乘以 1 都等於它本身(例如 5 * 1 = 5)+ 或 .concat()),單位元素是空字串 "",因為任何字串與空字串串接後都維持不變(例如 "hello" + "" = "hello").concat()),單位元素是空陣列(例如 [1, 2].concat([]) 的結果仍然是 [1, 2])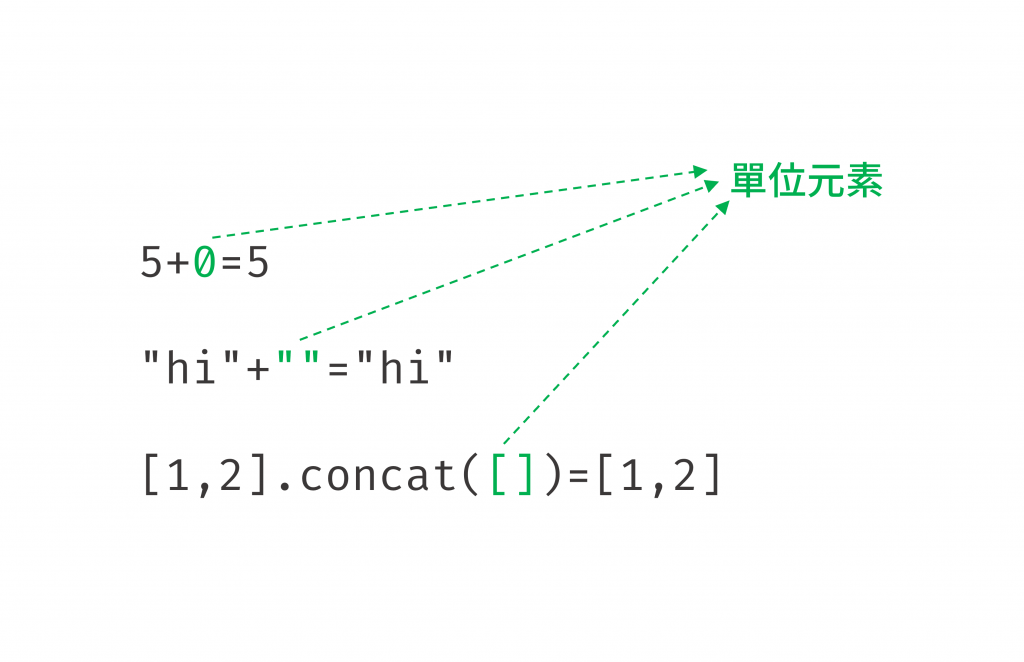
圖 4 單位元素就像透明元素(資料來源: 自行繪製)
單位元素不僅是個理論上的概念,在實務中,它為我們的程式碼提供了一個安全的起點,同時也是一種強大的容錯保護機制。
它的意義包含以下兩點:
1. 作為沒有東西時的安全預設值/初始值
單位元素為「空集合」的情況提供了一個有意義且邏輯一致的結果。
假設我們要計算一個數字陣列的總和,當陣列為空時,sum([]) 應該回傳什麼?如果我們回傳 null 或 undefined,程式就必須額外處理特殊情況。但如果我們將空陣列的總和定義為加法操作的單位元素 0,這在邏輯上是完全一致的(「無物之和」即為零),並且函式始終回傳一個 Number 型別的值。這避免了程式潛在的型別錯誤,也與「空物件模式」的設計思想相符。
另舉個實際範例,當我們為 settings 函式的參數定義預設值時,我們就可定義單位元素來避免錯誤,這樣當使用者沒有輸入該參數時,我們的函式運作也不會因為找不到值而出錯。
const settings = (prefix="", overrides=[], total=0) => ...
2. 作為累加器的初始值
單位元素是為累加運算而生的。當我們使用 Array.reduce 這類方法時,initialValue 參數正是單位元素所扮演的角色。它為整個運算提供了一個安全起點。如果我們處理的集合是空的,reduce 會安全地回傳這個 initialValue,而不是拋出 TypeError 錯誤。這解決了當集合為空時,reduce 卻找不到起點的問題。
因此,單位元素為「對零個元素進行操作」這種情況提供了一個有意義且邏輯一致的結果,讓我們的聚合函式更健壯和完備。
補充:Monoid 不要求交換律 (commutativity)。也就是說,a • b 不必等於 b • a。
理解 Monoid 的規則後,我們可能會發現,Monoid 在日常開發中無處不在。這裡會舉例一些隱藏在我們周遭的 Monoid,並為每一個例子明確指出其集合、操作和單位元素。
但必須說明的是,舉例有其局限性,Monoid 是個抽象概念,當我們舉出具體例子時,就侷限了抽象概念的可能性,因此,這些具體實例無法完全代表 Monoid,不過我覺得看越多舉例、越能從中統整出共同模式,藉此能更了解 Monoid 的樣貌。
+
*
這說明了同一個集合(數字)可以根據不同的操作形成不同的 Monoid。
+ 或 .concat()
""
.concat()
[]
只要我們處理的是陣列的合併,而不是元素的修改,它就完美符合 Monoid 的定義。
同一個集合({true, false})可透過不同的操作和單位元素,構成兩個截然不同的 Monoid。
&& (AND)true
單位元素之所以是 true,是因為對於任何布林值 x,x && true 的結果永遠是 x。範例如下:
const a = false;
console.log(a && true); // false
console.log(true && a); // false
const b= true;
console.log(b && true); // true
console.log(true && b); // true
|| (OR)false
單位元素之所以是 false,是因為對於任何布林值 x,x || false 的結果永遠是 x。範例如下:
const a = false;
console.log(a || false); // false
console.log(false || a); // false
const b= true;
console.log(b || false); // true
console.log(false || b); // true
這是更抽象但對 Functional Programming 概念非常重要的例子。
(A -> A)
x => f(g(x))
x => x
任何函式與恆等函式組合,結果都等於該函式本身,符合單位元素的定義。
下表總結了上述常見的 JavaScript Monoid。將這些具體範例並列,可以讓我們更清晰地看到它們背後共享的抽象結構。即使它們處理的資料型別和執行的操作各不相同,但「集合、操作、單位元素」這一核心模式始終如一。
| Monoid 名稱 | 集合 (型別) | 二元操作 (a • b) | 單位元素 (e) |
|---|---|---|---|
| 加法 (Sum) | Number |
a + b |
0 |
| 乘法 (Product) | Number |
a * b |
1 |
| 字串 (String) | String |
a.concat(b) |
"" |
| 陣列 (Array) | Array |
a.concat(b) |
[] |
| 全真 (All) | Boolean |
a && b |
true |
| 任一真 (Any) | Boolean |
a || b |
false |
| 函式組合 (Endo) | Function (a -> a) |
x => f(g(x)) |
x => x |
補充:還有 Min/Max Monoid,分別使用
Infinity/-Infinity作為單位元素。
圖 5 Monoid 三要素示意圖(資料來源: 自行繪製)
Array.reduce()在 JavaScript 開發者眼中,Array.reduce() 是一個用於將陣列「歸納」為單一值的強大工具。reduce 方法的設計,可說是 Monoid 模式的完美體現。
我們可以建立一個清晰的對應關係:
reduce 方法接收的回呼函式 (accumulator, currentValue) =>...,正是我們針對集合內元素的二元操作reduce 方法的第二個可選參數 initialValue,正是我們的單位元素當我們使用 reduce 時,實際上是在告訴 JavaScript:「這裡有一個陣列(集合的元素),請使用這個函式(二元操作)和這個初始值(單位元素),將它們全部摺疊成一個值。」
// 加法 Monoid
const numbers = [2, 1, 3, 4];
const sum = numbers.reduce((acc, val) => acc + val, 0);
// 字串 Monoid
const words = ['Monoid', ' ', 'is', ' ', 'awesome'];
const sentence = words.reduce((acc, val) => acc + val, ''); // 單位元素是 ""
console.log(sentence); // 輸出: "Monoid is awesome"
當我們提供單位元素作為 initialValue 時,reduce 就能安全地處理空陣列:
const emptyNumbers = [];
const sumOfEmpty = emptyNumbers.reduce((acc, val) => acc + val, 0);
console.log(sumOfEmpty); // 輸出: 0,而不是錯誤
這證明了 Monoid 不僅是一個理論概念,它還為我們日常使用的工具提供了健壯、可預測的行為模式。
接下來要透過反例來更理解 Monoid 的規則,再稍微介紹 Monoid 和其他設計模式的關聯。
讓我們看看為什麼某些常見的操作無法構成 Monoid。
reduce 處理一個空陣列的減法,我們找不到一個安全的初始值可以傳入,這使得處理邊界情況(如空集合)變得困難且容易出錯。reduce 的核心機制——將上一步的結果作為下一步的輸入——在這裡會因為型別不匹配而中斷。組合的鏈條在第一步就斷裂了,因為後續的操作可能無法處理 2.5 這種非整數的型別。由反例可知,Monoid 的規則不是隨意設定的學術要求,它們共同確保了一種穩定、可預測且高度靈活的組合行為,是許多強大程式設計模式能成立的基礎。
許多我們聽過的設計模式,其核心就是 Monoid。
複合模式讓我們將物件組合成樹狀結構,並以統一的方式對待單一物件和物件組合。這與 Monoid 的思想相同。一個介面或類別可以形成一個 Monoid,前提是其公開方法的回傳型別本身就是 Monoid。
Order 物件的 getPrice() 方法回傳一個數字(Sum Monoid)。一個 CompositeOrder(包含多個子訂單)的 getPrice() 就是將所有子訂單的價格相加。一個空的 CompositeOrder 的價格就是 0(Sum Monoid 的單位元素)空物件模式會提供一個具有預設「無操作」行為的替代物件,來避免處理 null 參考。這個「無操作」的物件,其實就是 Monoid 的單位元素。
NullObject 本身。它在組合中不會產生任何效果if (result!= null) 檢查,不如回傳一個 NullString 物件,其 toString() 方法回傳 ""(String Monoid 的單位元素)。無論結果如何,呼叫端都可以安全地進行字串串接命令模式將請求封裝成一個物件。當這些命令物件可以被組合時,它們就形成了一個 Monoid。
Monoid 本質上是由三個簡單規則所定義的組合模式:

圖 6 Monoid 的定義(資料來源: The Functional Programmer's Toolkit - Scott Wlaschin)
那這跟 Functional Programming 有什麼關係?為什麼要花一整篇文章來介紹它?
Monoid 是 FP 世界中「組合」的基礎。FP 的核心思想,就是將大型、複雜的問題,分解成微小、單純、可預測的函式,然後再像樂高積木一樣將它們組合起來。當一個複雜運算問題可以輕易的拆解與組合,我們的注意力就可以更集中在微小的運算函式上,確保每個小的函式都運作正常,最後再組合出大型且複雜的運算邏輯。
而 Monoid 正是為這種組合行為提供了一套最基本、最可靠的「遊戲規則」。它告訴我們,只要滿足這三條簡單的法則,我們就可以安心地、大規模地組合事物,無論是數字、字串,甚至是函式本身。
介紹 Monoid 的目的,是為了建立一個關鍵的心智模型:在 FP 的世界裡,強大的抽象工具都必須遵守簡單的法則。當我們接下來要探索 Functor、Applicative 和 Monad 時,會發現它們也都有各自的規則,其精神與 Monoid 一脈相承。它們都是在玩「組合」這件事,只是組合的對象和情境不同。
現在我們瞭解了 Monoid 的威力,透過 結合律 與 單位元素律,它為我們提供了一個穩健且通用的介面,來組合相同型別的值。這就是昨天文章第一個問題的答案:一種有原則的聚合之道。
但還有第二個問題:該如何將一個函數應用於容器內部的值?
Monoid 處理的是「值的組合」 (T, T) -> T,而接下來我們需要的是一個能將函數 (A -> B) 套用到容器 F<A> 上,並得到 F<B> 的機制。這機制就是 Functor,會在下篇文章介紹。
