在之前解的題目中我們可以看到leetcode輸入已經給建好的圖，但這些二維陣列有些像是Leetcode 695只要上下左右做BFS、DFS到最右下角就好，有些是像Leetcode 797陣列的列是目前節點，欄是與目前節點相連的節點，所以今天來理解建圖。

隱式建圖 implicit graph

像Leetcode 695或是Leetcode 1091輸入的二維陣列就是一張代表相對位的地圖，並用0、1代表該位置屬性。

鄰接串列 Adjacency List

有向鄰接串列

像Leetcode 797，我們列是目前節點，欄是目前節點能通往的節點。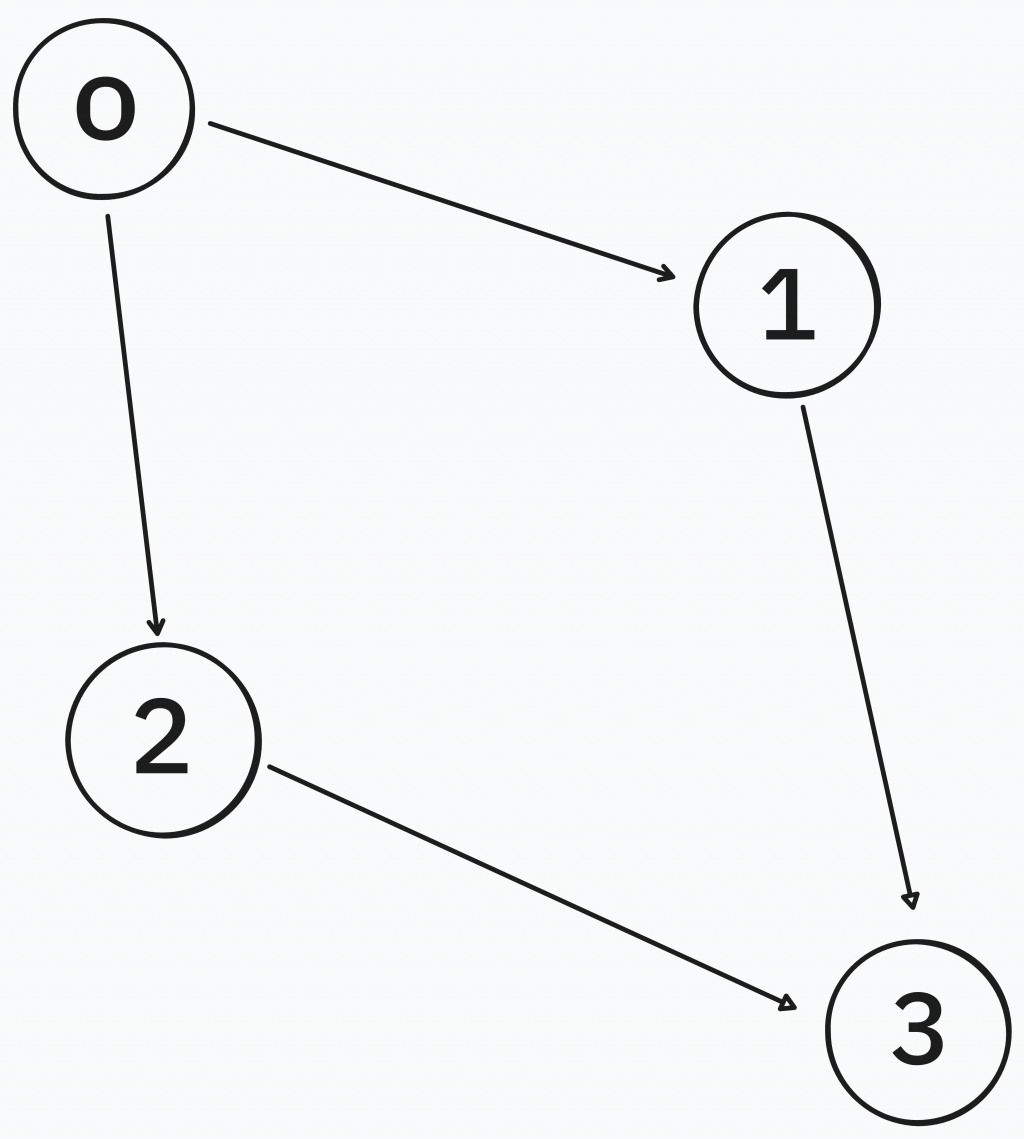

如果要用鄰接串列建上圖，key目前節點，value存目前可以走的點，(0,1)如果是有向代表節點0走到節點1

fn build_graph_directed(n: usize, edges: &[(usize, usize)]) -> Vec<Vec<usize>> {
    let mut g = vec![vec![]; n];
    for &(u, v) in edges {
        g[u].push(v);
    }
    g
}

fn main() {
    let n = 4;
    let edges = vec![(0, 1), (0, 2), (1, 3), (2,3)];
    let g = build_graph_directed(n, &edges);
    println!("{:?}", g); 
}

// [
//[1, 2], //節點0 可到 1 2
//[3],    //節點1 可到 3
//[3],    //節點2 可到 3
//[]      //節點3 沒路了
//]

無向鄰接串列

如上面有向建法但注意(0,1)有邊代表節點1也能走到節點０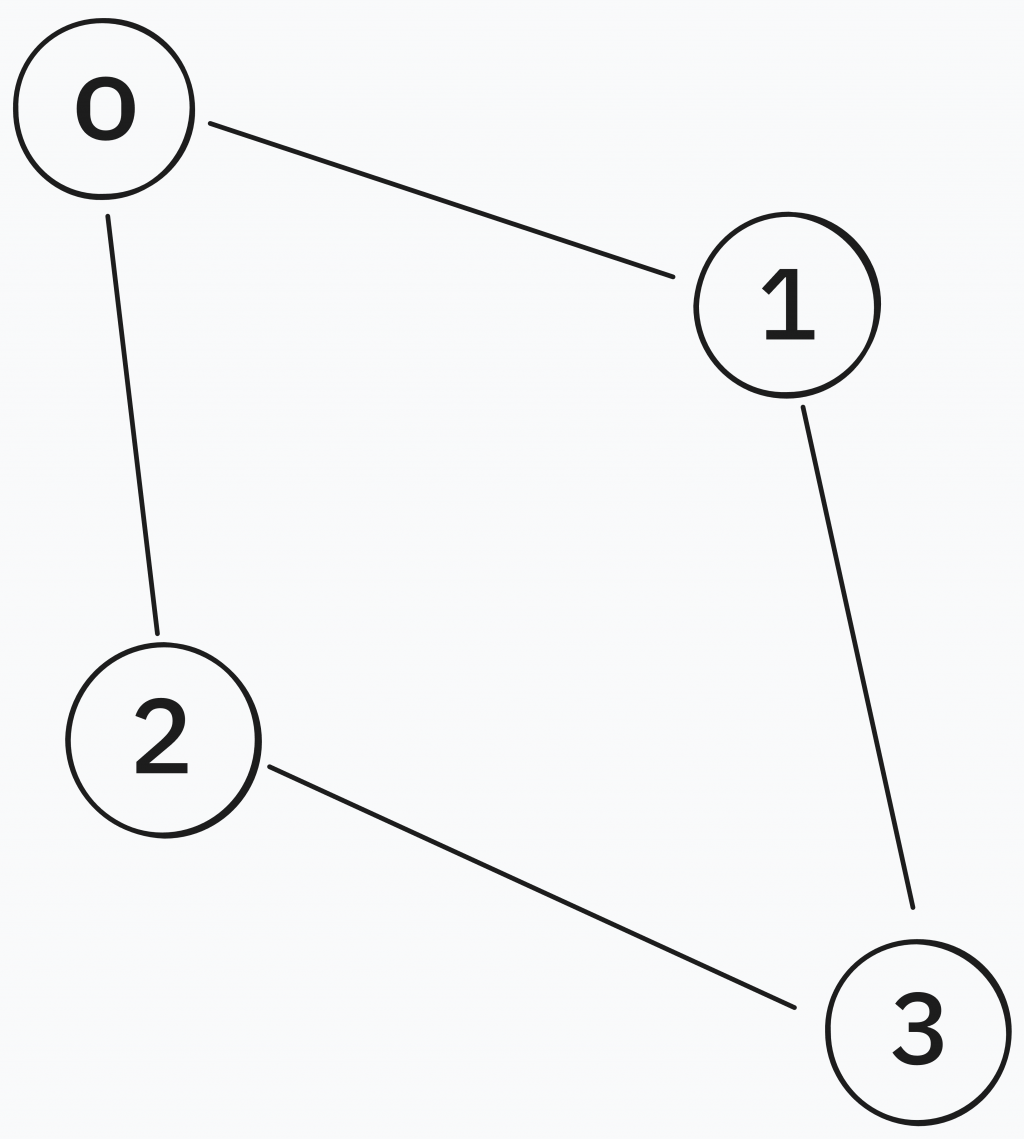

fn build_graph_undirected(n: usize, edges: &[(usize, usize)]) -> Vec<Vec<usize>> {
    let mut g = vec![vec![]; n];
    for &(u, v) in edges {
        g[u].push(v);
        g[v].push(u);
    }
    g
}

fn main() {
    let n = 4;
    let edges = vec![(0, 1), (0, 2), (1, 3), (2,3)];
    let g = build_graph_undirected(n, &edges);
    println!("{:?}", g); 
}
//[
//[1, 2], //節點0 可到 1 2
//[0, 3], //節點1 可到 0 3
//[0, 3], //節點2 可到 0 3
//[1, 2]  //節點3 可到 1 2
//]

鄰接矩陣 Adjacency Matrix

鄰接串列只記錄有連到的節點，鄰接矩陣把全部是否有邊到記錄下來。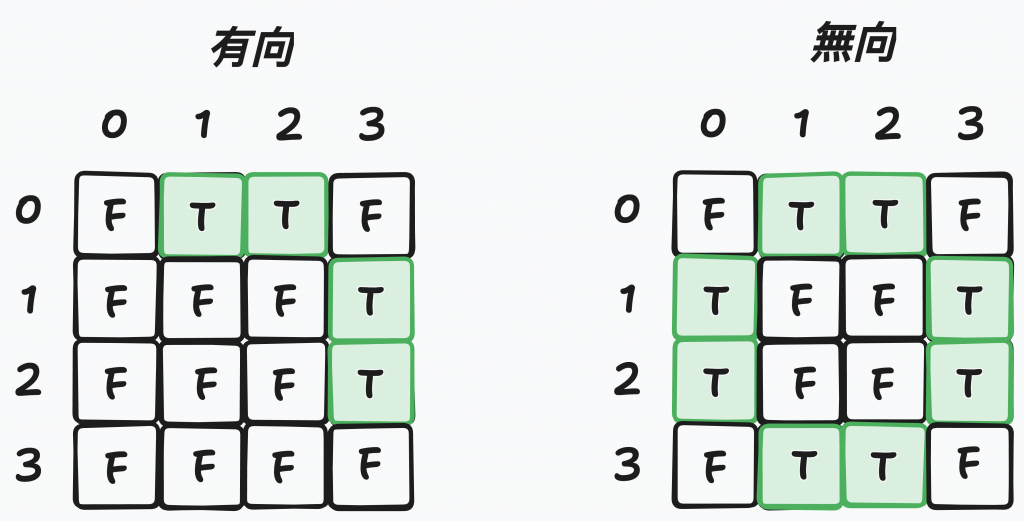

fn build_matrix(n: usize, edges: &[(usize, usize)]) -> Vec<Vec<bool>> {
    let mut m = vec![vec![false; n]; n];
    for &(u, v) in edges {
        m[u][v] = true;
        // 無向：
        // m[v][u] = true;
    }
    m
}

fn main() {
    let n = 4;
    let edges = vec![(0, 1), (0, 2), (1, 3), (2,3)];
    let g = build_matrix(n, &edges);
    println!("{:?}", g);
}

Adjacency List V.S. Adjacency Matrix

照慣例我們刷個一題來練習

Leetcode 1971. Find if Path Exists in Graph

題目：給一組兩兩相鄰的節點，判斷source和destination節點是否有相連

輸入：n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2

輸出：true

解法：只要把給的節點建好圖，就能用BFS遍歷判斷是否有路能通

Adjacency List建圖解法

use std::collections::{VecDeque,HashSet};
impl Solution {
    pub fn valid_path(n: i32, edges: Vec<Vec<i32>>, source: i32, destination: i32) -> bool {
        let mut adjance_list=vec![vec![];n as usize];
        for edge in edges {
            adjance_list[edge[0] as usize].push(edge[1]);
            adjance_list[edge[1] as usize].push(edge[0]);
        }
        let mut deque=VecDeque::new();
        let mut set=HashSet::new();
        deque.push_back(source);
        while let Some(c_n) = deque.pop_front() {
            if c_n==destination {
                return true
            }
            for &m in &adjance_list[c_n as usize] {
                if(set.contains(&m)){
                    continue
                }
                deque.push_back(m);
                set.insert(m);
            }
        }
        return false
    }
}

Adjacency Matrix建圖解法

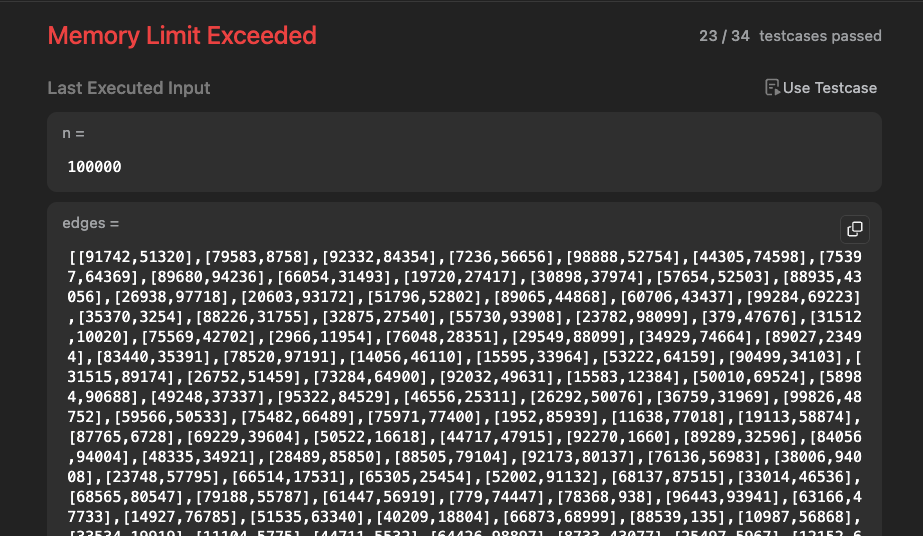
當n=100000時Memory Limit Exceeded

use std::collections::{VecDeque,HashSet};
impl Solution {
    pub fn valid_path(n: i32, edges: Vec<Vec<i32>>, source: i32, destination: i32) -> bool {
        let mut adjance_matrix=vec![vec![false;n as usize];n as usize];
        for edge in edges {
            adjance_matrix[edge[0] as usize][edge[1] as usize]=true;
            adjance_matrix[edge[1] as usize][edge[0] as usize]=true;
        }
        let mut deque=VecDeque::new();
        let mut set=HashSet::new();
        deque.push_back(source);
        while let Some(c_n) = deque.pop_front() {
            if c_n==destination {
                return true
            }
            for i in 0..n as usize{
                if adjance_matrix[c_n as usize][i] {
                    if(set.contains(&(i as i32))){
                        continue
                    }
                    deque.push_back(i as i32);
                    set.insert(i as i32);
                }
            }
        }
        return false
    }
}

如何判斷稀疏圖或稠密圖

1. 稀疏圖 (Sparse Graph)：

   1. 邊數 E 遠小於 V²。

   2. 典型情況：E ≈ V 或 E ≈ V log V。

   3. 一個點平均只跟「少數」點相連。

2. 稠密圖 (Dense Graph)：

   1. 邊數 E 接近 V²。

   2. 典型情況：E ≈ V²。

   3. 幾乎每對點之間都有邊。

Day28 總結

1. 如何透過輸入相鄰的節點建圖
2. Adjacency List 稀疏圖 (Sparse Graph)
3. Adjacency Matrix 稠密圖 (Dense Graph)

參考

1. https://www.geeksforgeeks.org/dsa/comparison-between-adjacency-list-and-adjacency-matrix-representation-of-graph/