題目

題目說他會給我兩個單字，分別是word1和word2，我需要做的是把word1轉換成word2，然後我需要給的東西是轉換的最小操作次數。
然後我可以對word1做的操作有三個動作:

1. 插入一個字元
2. 刪除一個字元
3. 替換一個字元

Example 1:
Input: word1 = "horse", word2 = "ros"
Output: 3
說明:
horse -> rorse (把 'h' 替換成 'r')
rorse -> rose (移除 'r')
rose -> ros (移除 'e')

想法

這題呢我想了很久，但是不知道從何下手，所以我就問了Gemini讓他給我一點思考方向

所以我要先建一個dp[]來表示word1前i個字母變成word2前j個字母需要的最少步數，
如果word1 是空字串，要變成word2 的前j個字母，就要插入j次，所以dp[0][j] = j。
如果word2 是空字串，要把word1 的前i個字母變成空字串，就要刪除 i 次，所以dp[i][0] = i。
如果word1[i-1] == word2[j-1]，那就不需要操作，直接dp[i][j] = dp[i-1][j-1]。
如果word1[i-1]不等於word2[j-1]，那就要執行刪除、插入或替換這三個操作，然後去選最小的，接著一步一步地做完，最後dp[m][n]就是最少的操作次數了。

程式碼

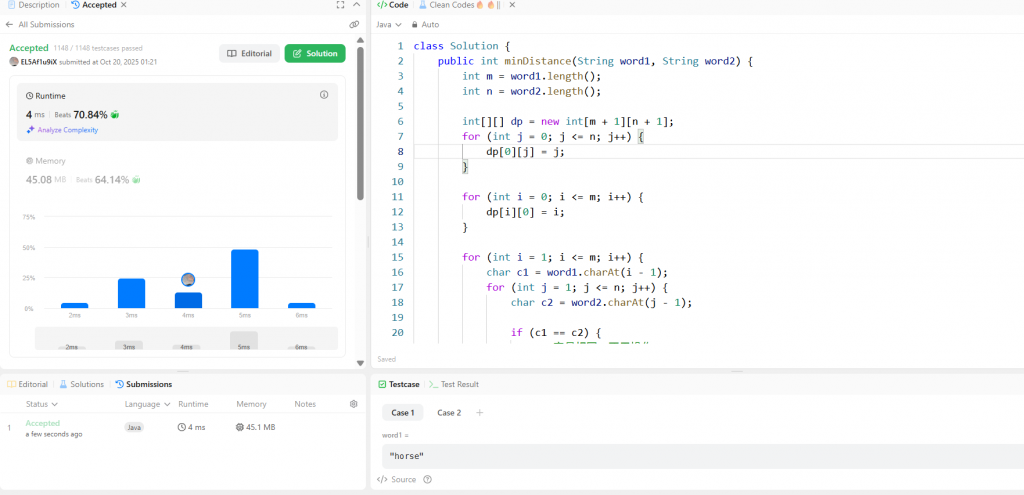
class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();

        int[][] dp = new int[m + 1][n + 1];
        for (int j = 0; j <= n; j++) {
            dp[0][j] = j;
        }
        
        for (int i = 0; i <= m; i++) {
            dp[i][0] = i;
        }

        for (int i = 1; i <= m; i++) {
            char c1 = word1.charAt(i - 1);
            for (int j = 1; j <= n; j++) {
                char c2 = word2.charAt(j - 1);

                if (c1 == c2) {
                    // 字母相同，不用操作
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    // 字母不同，三種操作取最小
                    int replaceCost = dp[i - 1][j - 1]; // 替換
                    int deleteCost = dp[i - 1][j];      // 刪除
                    int insertCost = dp[i][j - 1];      // 插入

                    dp[i][j] = 1 + Math.min(replaceCost, Math.min(deleteCost, insertCost));
                }
            }
        }

        return dp[m][n];
    }
}

參考:https://leetcode.com/problems/edit-distance/solutions/3230662/clean-codes-full-explanation-dynamic-programming-c-java-python3

執行成功