題目

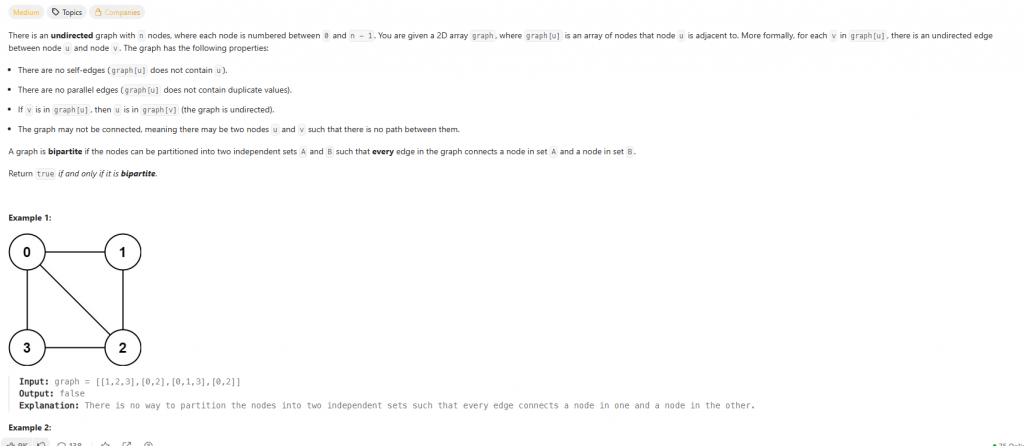
題目給了我一個無向圖 (Undirected Graph)。圖中的節點編號從0到n-1。
graph[i]是一個列表，包含了所有與節點i相連的節點，所以graph是一個鄰接串列。
然後我要做的就是判斷這個圖是不適二分圖。

二分圖

如果我們可以將圖中所有的頂點分成兩個獨立的集合（A組和B組），並且滿足這些條件：

1. 兩個集合A和B是互斥的（一個節點要嘛在A組，要嘛在B組，不能同時在兩組）。
2. 兩個集合A和B包含了所有的頂點。
3. 圖中的每一條邊，所連接的兩個頂點必須分別來自A組和B組。
4. 絕對不存在任何一條邊是連接「A 組內部的兩個點」或「B 組內部的兩個點」的。

他想說的就是A組裡的所有節點，彼此之間不能有邊相連，B組也是。所有的邊都必須跨越A組和B組。

然後他通常都是用染色的概念去思考的:
我們用兩種顏色（例如紅、藍）去塗圖上的節點。如果能做到「所有相鄰節點顏色都不同」，這個圖就是二分圖。

染色規則：
如果節點 A 是紅色，則 A 的所有鄰居都要是藍色。
如果節點 B 是藍色，則 B 的所有鄰居都要是紅色。

不是二分圖的情況：
當出現「相鄰節點被迫同色」的衝突。
這個情況通常發生在奇數長度的環中。
所以只要一個圖包含奇數環，就一定無法完成正確染色，因此就可以知道他不是二分圖。

程式碼

class Solution {
    int[] color; // 儲存每個節點的顏色，0=未染色, 1=紅, -1=藍

    public boolean isBipartite(int[][] graph) {
        int n = graph.length;
        color = new int[n];

        // 圖可能有多個連通分量，因此每個節點都要檢查一次
        for (int i = 0; i < n; i++) {
            if (color[i] == 0) {      // 新的未染色區域
                if (!dfs(i, graph, 1)) // 從 i 開始染色，任意給顏色 1
                    return false;   // 如果發現衝突，代表整張圖不是二分圖
            }
        }
        return true; // 所有部分都染色成功，是二分圖
    }

    // 染色當前節點，檢查鄰居
    boolean dfs(int node, int[][] graph, int currentColor) {
        color[node] = currentColor; // 染色當前節點

        for (int neighbor : graph[node]) {
            if (color[neighbor] == 0) {
                // 鄰居未染色，用相反顏色遞迴染色
                if (!dfs(neighbor, graph, -currentColor))
                    return false;
            } 
            // 鄰居顏色相同，代表衝突
            else if (color[neighbor] == currentColor) {
                return false;
            }
        }
        return true; 
    }
}

程式碼引用:
https://leetcode.com/problems/is-graph-bipartite/solutions/7284419/100-beat-depth-first-search