題目

他給一個 n x n 的二維矩陣grid，0代表可以走的格子，1代表障礙。
要找出從左上角 (0,0) 到右下角 (n-1, n-1) 的最短路徑長度。
然後我可以往 8 個方向上下左右斜角移動。

如果無法到達終點，回傳 -1。
這題是一個無權圖最短路徑問題，所以選擇用BFS找最短距離是一個很好的選擇。
每一層的擴展，就代表走一步。
然後因為BSF是每一層的擴展，就代表走一步，所以最先到終點的就醫定是最短路徑。

程式碼

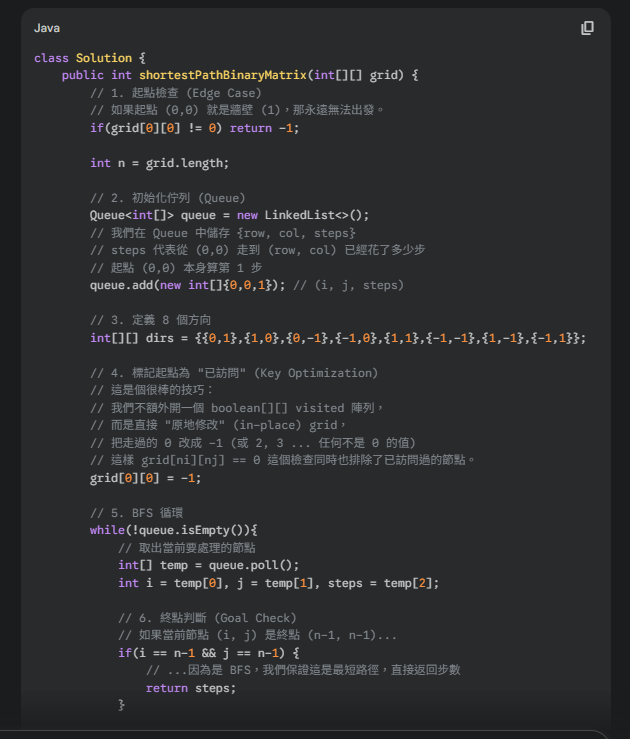
class Solution {
    public int shortestPathBinaryMatrix(int[][] grid) {
        int n = grid.length;
        // 如果起點或終點被擋住直接回傳-1
        if (grid[0][0] == 1 || grid[n-1][n-1] == 1) return -1;

        // 八個方向 (上下左右 + 四個斜角)
        int[][] dirs = {{1,0},{-1,0},{0,1},{0,-1},{1,1},{1,-1},{-1,1},{-1,-1}};
        Queue<int[]> q = new LinkedList<>();
        q.offer(new int[]{0, 0});
        grid[0][0] = 1; // 用grid儲存步數 ，避免重複走訪

        while (!q.isEmpty()) {
            int[] cur = q.poll();
            int r = cur[0], c = cur[1];
            int dist = grid[r][c];

            // 到達終點
            if (r == n - 1 && c == n - 1) return dist;

            // 擴展八個方向
            for (int[] d : dirs) {
                int nr = r + d[0], nc = c + d[1];
                // 檢查邊界與障礙
                if (nr >= 0 && nc >= 0 && nr < n && nc < n && grid[nr][nc] == 0) {
                    grid[nr][nc] = dist + 1; // 紀錄步數
                    q.offer(new int[]{nr, nc});
                }
            }
        }
        return -1; // 無法到達
    }
}

程式碼引用:
https://leetcode.com/problems/shortest-path-in-binary-matrix/solutions/7163990/simple-bfs-queue-approach-beats-95-of-solutions