題目

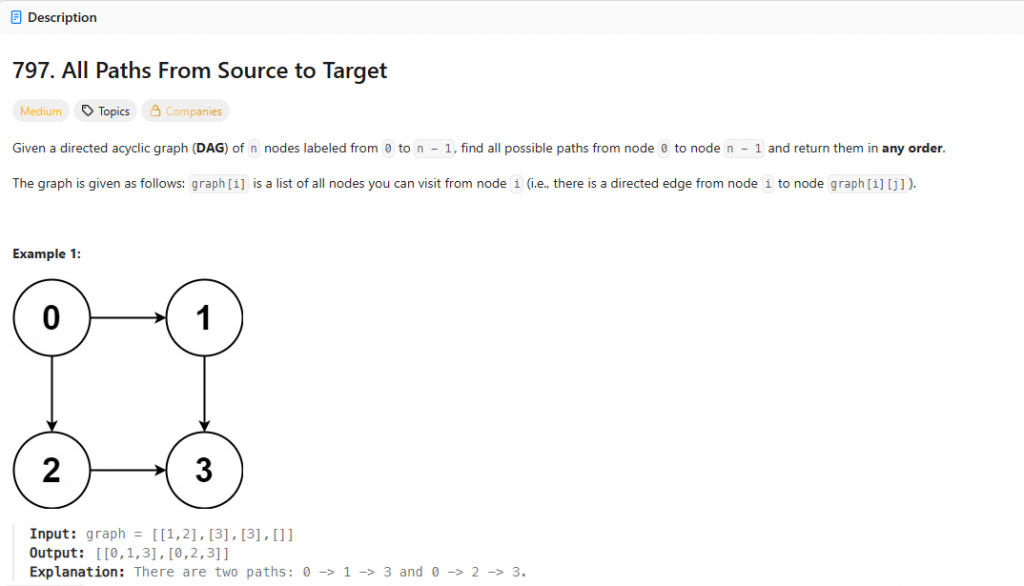
這個題目說他會給我一個有向無環圖(DAG)，包含了n個節點，從0~n-1。
graph[i]是一個列表，包含了所有我可以從節點i訪問到的節點。所以graph 是一個鄰接串列。
我的任務是找出所有從源點0到終點 n-1的所有可能路徑，並以任意順序返回它們。

Example 1:
Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
解釋:
graph 表示：
從 0 可以到 1 和 2，
從 1 可以到 3，
從 2 可以到 3，
從 3 哪裡都去不了。
然後目標是從0到3，所以路徑是[0,1,3],[0,2,3]這兩種。

程式碼

這是我引用leetcode上分享的程式碼，然後他有分享兩種解法，一個是DFS另一個是BFS，那因為前面的文章有說到如果是找出所有路徑的問題類型的話，DFS通常都會比BFS來的快，所以我就選擇來理解DFS的這個程式碼。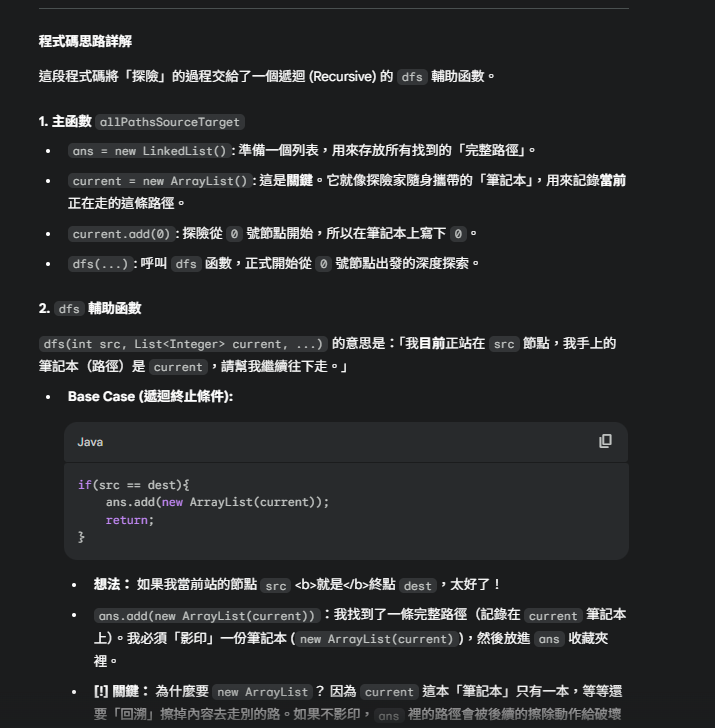

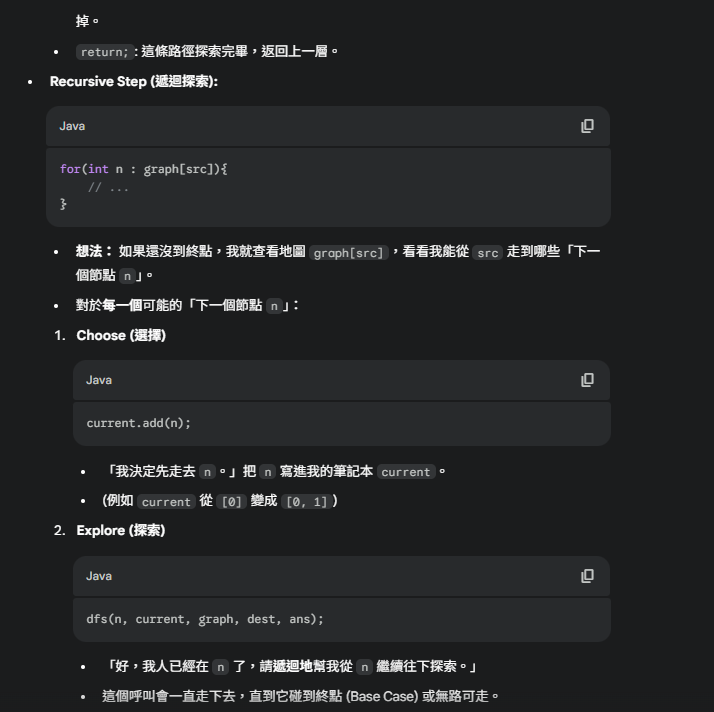
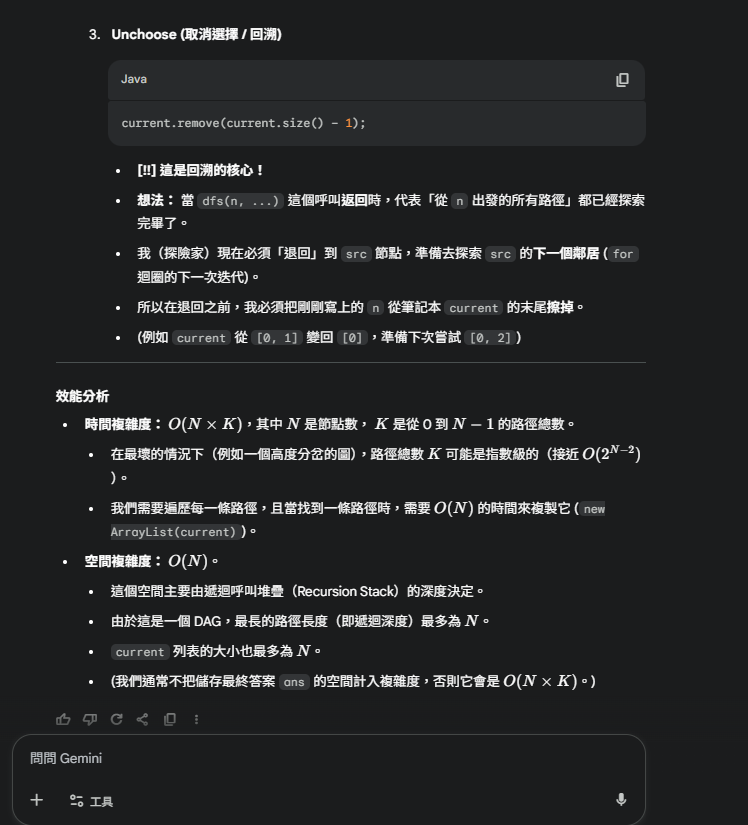
最後我自己理解了一下，註解的程式碼

class Solution {
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        
        List<List<Integer>> ans = new LinkedList<>(); //存放所有從0到n-1的路徑
        List<Integer> current = new ArrayList<>(); // 記錄目前走過的節點（當前路徑）
        current.add(0); // 從節點 0 開始
        // 呼叫DFS，從0出發，目標是 graph.length - 1
        dfs(0, current, graph, graph.length - 1, ans);
        return ans;
    }

    private void dfs(int src, List<Integer> current, int[][] graph, int dest, List<List<Integer>> ans) {
        // 如果目前節點 == 目標節點，表示找到了一條完整路徑
        if (src == dest) {
            // 要 new 一份 current 的複本，否則之後回溯會修改內容
            ans.add(new ArrayList<>(current));
            return;
        }

        // 遍歷目前節點src的所有相鄰節點 n
        for (int n : graph[src]) {
            current.add(n);  // 把這個相鄰節點加入當前路徑
            dfs(n, current, graph, dest, ans);  // 繼續往下遞迴
            current.remove(current.size() - 1); 
        }
    }
}

引用的程式碼:https://leetcode.com/problems/all-paths-from-source-to-target/solutions/2969408/simple-java-solution-using-dfs-and-bfs-100-faster