
時間序列是一組按時間順序排列的資料點
比如:
時間序列資料有三個主要組成部分。
在時間序列中記錄的長期緩慢變化/方向。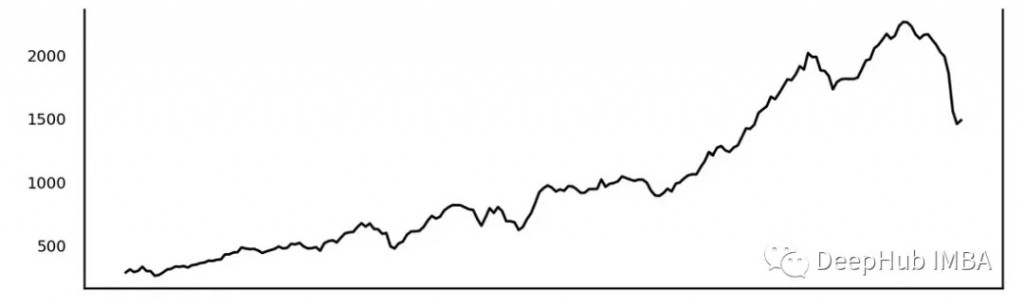
季節性是在固定時間內發生的時間序列中的迴圈模式。
下面的時間序列顯示了季節性,在每個週期中,都處於底部和峰值,模式相似。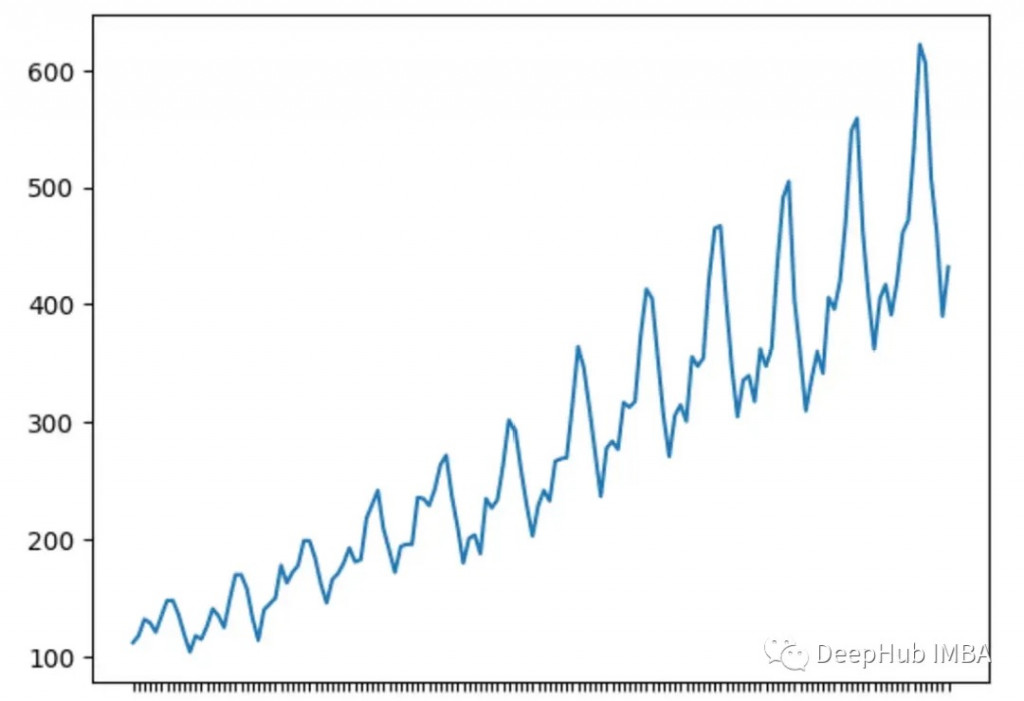
這是一個時間序列的模式,完全是隨機的,不能用趨勢或季節成分來解釋。
時間序列分解是將時間序列分解為其組成部分的過程,即趨勢,季節性和殘差。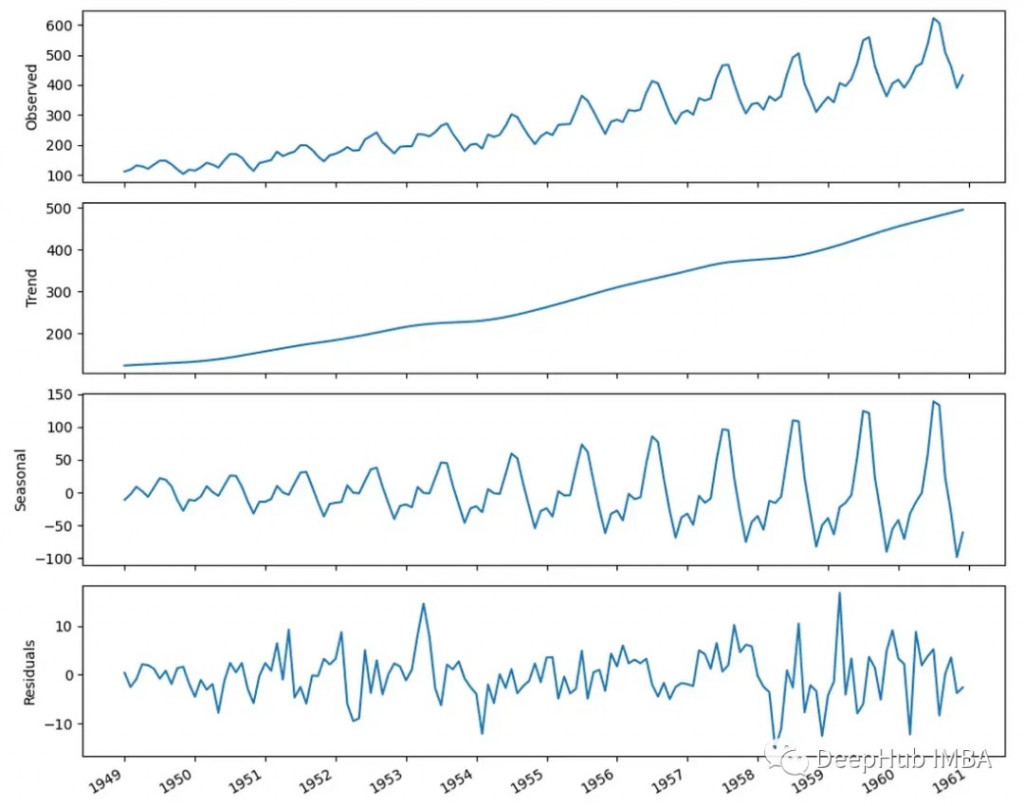
在上圖顯示了時間序列資料,資料下面的圖中被分解為其組成部分。
“殘差”顯示的是時間序列中無法用趨勢或季節性解釋的模式。這些表示資料中的隨機性。
我們可以使用如下所示的statmodels庫來分解時間序列。
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import STL
df = pd.read_csv("time-series-data.csv")
decomposition = STL(df['x'], period=12).fit()
decomposition 可以進一步繪製如下:
fig, (ax1, ax2, ax3, ax4) = plt.subplots(nrows=4, ncols=1, sharex=True,figsize=(10,8))
ax1.plot(decomposition.observed)
ax1.set_ylabel('Observed')
ax2.plot(decomposition.trend)
ax2.set_ylabel('Trend')
ax3.plot(decomposition.seasonal)
ax3.set_ylabel('Seasonal')
ax4.plot(decomposition.resid)
ax4.set_ylabel('Residuals')
plt.tight_layout()
預測是基於歷史時間資料在以後時間上進一步預測資料點的過程。
這可以使用統計模型來完成,例如:
對於較大的資料集,使用以下提到的深度學習模型:
根據歷史時間序列資料預測未來資料點的時間段。
例如根據10年記錄的每日氣溫資料,預測下一週的氣溫。
在這種情況下,預測範圍是一週的時間。
時間序列預測模型主要由以下步驟組成:
下面是時間序列預測與迴歸任務的主要區別。
時間序列資料是有序的。這意味著觀察/資料點依賴於以前的觀察/資料點。因此,在模型訓練期間,資料點順序不會被打亂。
時間序列預測處理隨時間收集的資料。而回歸可以處理不同型別的資料。
基線模型是使用naïve對時間序列資料進行預測構建的最簡單的模型。作為比較其他預測模型的基線。
以下假設可用於建立基線模型:
準確預測的目的是最小化資料中預測值與實際值之間的差距。所以有各種錯誤指標用於監視和最小化這種差距。
常用的誤差指標如下:
平穩的時間序列是其統計性質不隨時間變化的序列,這些統計屬性包括:
變換可以認為是使時間序列平穩的數學過程。常用的變換有:
差分計算從一個時間步到另一個時間步的變化。有助於在時間序列資料中獲得恆定的均值。
要應用差分,我們只需從當前時間步長的值中減去之前時間步長的值。
一階差分:對資料應用一次的差分;二階差分:對資料應用兩次的差分
對數函式應用於時間序列以穩定其方差,但是對數變換後需要進行逆向變換,將最終的結果進行還原。
Augmented Dickey-Fuller (ADF) Test是一種用於時間序列資料的經濟統計學檢驗方法,用於確定一個時間序列是否具有單位根(unit root)。單位根表示時間序列具有非平穩性,即序列的均值和方差不隨時間變化而穩定。ADF測試的目的是確定時間序列是否具有趨勢,並且是否可以進行經濟統計學分析。
ADF測試的核心假設是,如果時間序列具有單位根,則序列是非平穩的。反之,如果序列不具有單位根,則序列是平穩的。ADF測試透過對序列進行迴歸分析來驗證這些假設。
我們可以直接使用statsmodels來進行這個檢驗
from statsmodels.tsa.stattools import adfuller
ADF_result = adfuller(time_series)
print(f"ADF Result Value: {ADF_result[0]}")
print(f"ADF Result p-value: {ADF_result[1]}")
是對時間序列中由不同時間步長隔開的值之間線性關係的度量。滯後是分隔兩個值的時間步數。
自相關函式(ACF)圖用於測試時間序列中的值是否隨機分佈或彼此相關(如果時間序列具有趨勢)。
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(time_series, lags = 20)
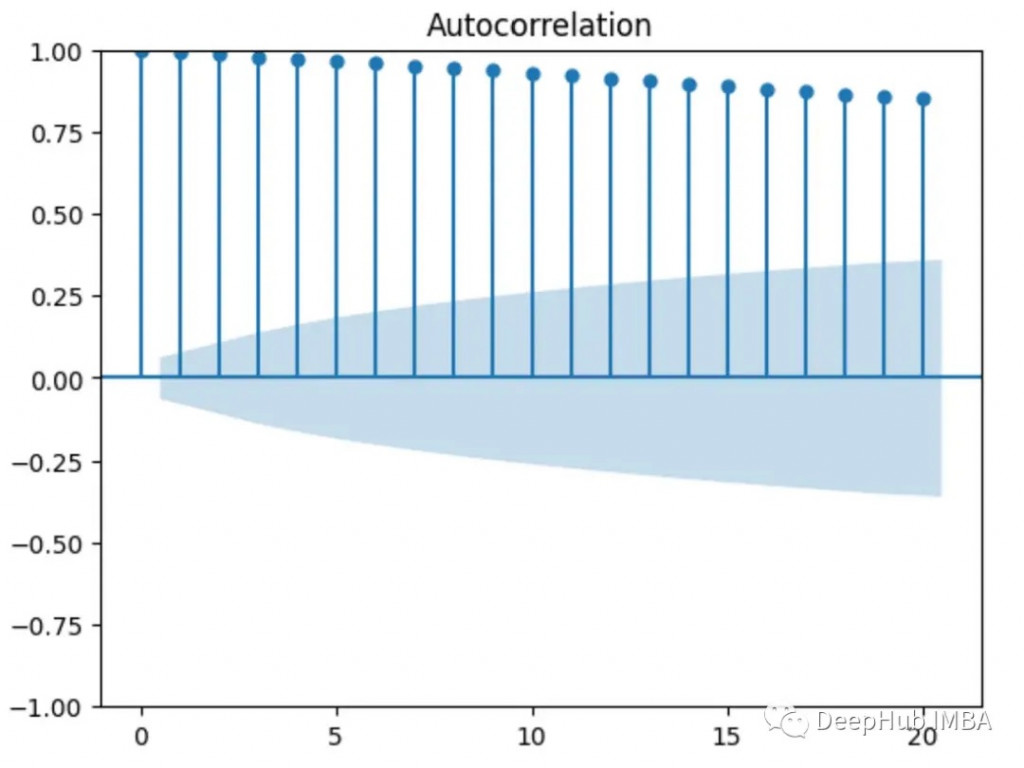
這裡的x軸上的值表示滯後,y軸上的值表示由滯後分隔的不同值之間的相關性。
如果y軸上的任何值位於圖的藍色陰影區域,則該值在統計上不顯著,比如下面的ACF圖顯示其值之間沒有相關性(除了第一個與自身相關的值)。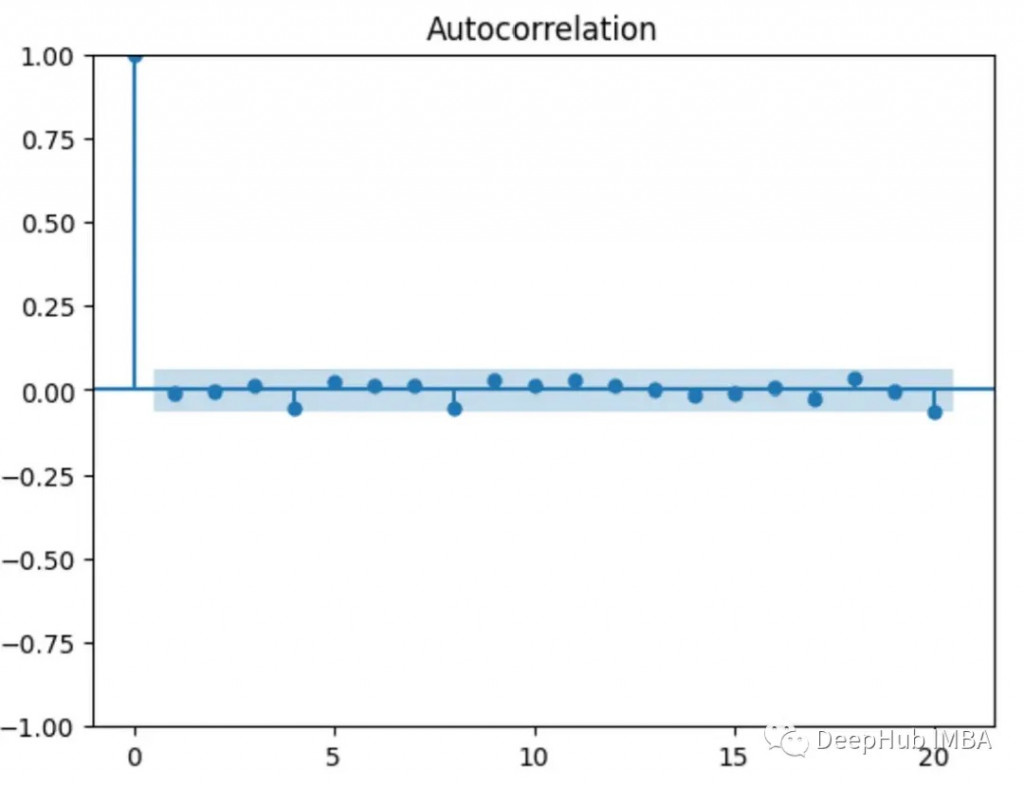
平滑方法(Smoothing Methods)是一種用於對時間序列資料進行平滑處理的技術,以便更好地觀察資料的趨勢和季節性成分。這些方法的目標是減少隨機噪聲,突出資料中的長期變化模式。
常見的有:移動平均法(Moving Average Method)、加權移動平均法(Weighted Moving Average Method)、指數平滑法(Exponential Smoothing Method)、季節性平滑法(Seasonal Smoothing Method)
靜態時間序列(Static Time Series):靜態時間序列是指資料在時間上沒有變化的情況下進行分析。也就是說,它假設觀測到的時間序列資料是固定的,沒有隨時間的推移而發生變化。在靜態時間序列中,我們通常關注資料的平均水平、趨勢和季節性等靜態特徵。常見的靜態時間序列模型包括平均數模型、指數平滑模型和ARIMA模型等。
動態時間序列(Dynamic Time Series):動態時間序列是指資料在時間上呈現出變化的情況下進行分析。也就是說,它認為觀測到的時間序列資料是隨時間變化的,並且過去的值對未來的值有影響。在動態時間序列中,我們關注資料的動態性、趨勢變化和週期性等動態特徵。常見的動態時間序列模型包括自迴歸移動平均模型(ARMA)、自迴歸積分滑動平均模型(ARIMA)和向量自迴歸模型(VAR)等。
靜態時間序列假設資料在時間上沒有變化,主要關注資料的靜態特徵。動態時間序列考慮資料在時間上的變化,並關注資料的動態特徵。靜態時間序列可以看作是動態時間序列的特例,當資料在時間上沒有變化時,可以將其視為靜態時間序列。
季節性(Seasonality)和迴圈性(Cyclicity)都是描述時間序列資料中重複出現的模式,但它們之間存在一些區別。
季節性是在較短的時間尺度內,由於固定或變化的季節因素引起的週期性模式,而迴圈性則是在較長時間尺度內,由於經濟或其他結構性因素引起的週期性模式。
季節性(Seasonality)是指時間序列資料中由於季節因素引起的重複模式。這種模式通常是在較短的時間尺度內(例如每年、每季度、每月或每週)出現的,並且在不同時間段內的觀測值之間存在明顯的相似性。季節性可以是固定的,即在每個季節週期內的模式相對穩定,例如每年夏天都有高溫;也可以是非固定的,即在季節週期內的模式可能有變化,例如某個季節的銷售量在不同年份間波動。
迴圈性(Cyclicity)是指時間序列資料中具有較長週期性的模式。這種模式的週期可以大於或小於季節週期,並且迴圈性的持續時間通常比季節性更長。迴圈性可能是由經濟、商業或其他結構性因素引起的,與季節性不同,迴圈性的模式不一定按照固定的時間間隔出現,而是根據外部因素的影響而變化。例如,房地產市場的週期性波動就是一個迴圈性的例子。
在銷售、流量或業務活動中,趨勢線能幫助團隊理解整體方向究竟是在上升、停滯,或已經開始轉折。這類分析通常需要長時間的連續資料並搭配平滑處理,才能看到真正的走勢。若資料能穩定更新並以視覺化方式呈現,決策的清晰度會大幅提升。
許多業務表現具有明顯的季節性,例如零售旺季、週期訂單、日夜時段的流量差異。這些固定模式需要透過時間序列拆解才能被看見,並用來判斷「什麼時候是自然波動、什麼時候是真正異常」。能夠以不同時間粒度(年、季、月、週)快速切換,對分析效率非常重要。
在高度波動的資料裡,移動平均或平滑處理能協助刪除噪音,讓分析者看清真正的變化方向。這對營運、財務、供應鏈等領域特別重要,因為決策往往不需要每個細枝末節,而是需要理解「整體往哪裡走」。
時間序列的異常點往往是營運與風險管理的關鍵訊號,例如訂單突然下跌、設備數據跳動、成本異常上升等。這些變化若能即時被捕捉,通常能比週期性報表更早發現問題。而建立這類機制通常需要多來源資料與穩定的更新流程。
以上這些場景要真正落地,其實並不僅僅是公式問題,而是需要一套能同時處理「資料整合、時間粒度切換、視覺化、異常比較」的分析流程。在這裡向大家推薦適合企業分析的分析軟體FineBI, 在時間序列相關的使用情境中相對直觀:可以自由切換時間粒度、拖拉產生多序列折線圖、整合不同資料來源並自動更新。對個人用戶也提供免費版本,適合把時間序列分析真正融入日常工作,而不是停留在概念層次。
