我寫了一個pseudocode用來算一個整數n(n>2)的正因數總和(不包括n本身)
使用的計算正因數總和公式如下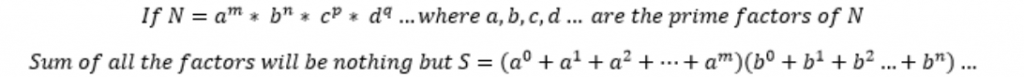
ex. 60做質因數分解後是2^2 * 3^1 * 5^1，則其所有正因數總和為(2^0 + 2^1 + 2^2)*(3^0 + 3^1)*(5^0 + 5^1)=(1+2+4)*(1+3)*(1+5)=168
pseudocode如下
最差時間複雜度會是O(根號n)，也就是當輸入n是質數的情況(若有說錯請指正)
最佳時間複雜度會是O(1)，也就是當輸入n是3的情況(若有說錯請指正)
若不考慮最差和最佳的情況，想請問版上大大平均時間複雜度會不會少於根號n
原因是時間複雜度我只關注跑最多次的地方，也就是for迴圈內的程式碼部分，但我發現因為短除法會使n一直變，所以for迴圈不會從2一直跑到根號n，實際跑的次數可能會更少。
以剛剛的60為例，第一次跑for迴圈(d=2)，它的範圍會是2~7，然後離開while之後n變成了15，所以到了for迴圈第二輪(d=3)，它的範圍會變成2~3，最後跳離for迴圈。原本看似要跑6次(7-2+1)，但實際上for迴圈內部只跑了兩次，這樣的話平均時間複雜度要怎麼評估呢?
已邀請的邦友 {{ invite_list.length }}/5
iThome鐵人賽
看影片追技術