在柏拉圖問題當中的第一部份是關於把題目數學化：
假如有N個球，每顆球的價值都不一樣。第一大為N，第二大為(N-1)，依此類推 … 最小為1（遊戲開始時只知道分數，不知道大小）。把這N顆球放到一個袋子裡，隨機拿球出來。現在的問題是：你要怎麼拿才可以拿到最大的球(N)呢？

現在我們研究「該利用怎麼樣的策略，得到最大的球(N)的機率會最大」。我們的策略是：
前(S-1)顆球完全不考慮，
從第S顆球起開始決定要不要拿，
如果第S顆球是前(S-1)顆最大的話，我們就「拿」，否則就到下一家。
可是，只剩最後一顆的情況下時，還是得拿最後那一顆。

根據我們的策略，其實是要研究在已知N是多少時，S為多少時，其得到最大的球(N)的機率會最高。

為了實際操作，我們先特殊化。設N=4，總共會有4!=24種，排列如下：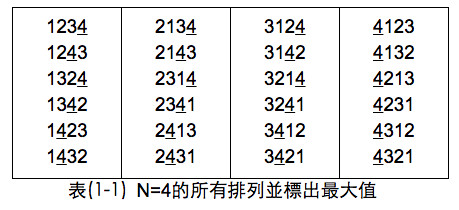

當S=2時，因為考慮到第一個值，導致第一個位置不能放4

(1)第二顆球大於第一顆球就拿。拿取到最大值的組合如下：

(2)第二個比第一個小，但是第三個比第一個大，所以拿到最大值。拿取到最大值的組合如下：

(3)最後一種是第二顆和第三顆都比第一顆小，到第四顆才比一顆大，所以拿到最大值。拿取到最大值的組合如下：

在第2個就取到最大值的有 6 種，計為 6/24
在第3個才取到最大值的有 3 種，計為 3/24
在第4個才取到最大值的有 2 種，計為 2/24

整理N=4，4≥S≥2的情況:

再討論N=5，5≥S≥2的情況: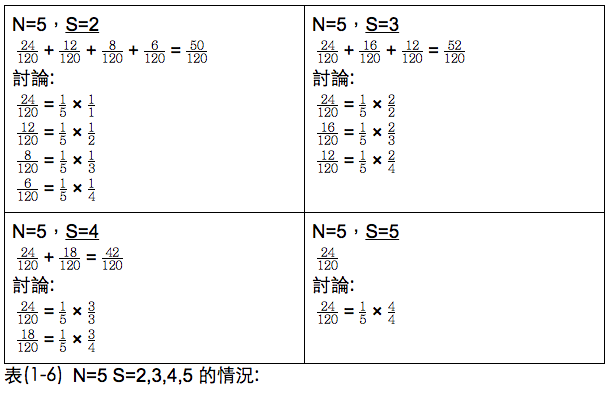

我們可以發現只要在每個數字乘以 (S-1)/N 後會形成調和數列，共有(N-S)項。可以寫成這樣：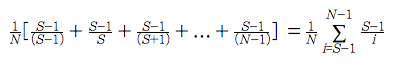

接下來就是要把可以把這個公式可以得到最大值機率最大的 N 和 S 的比例找出來了...

待續...