Regression

沿著昨天的結論，我想問的是，僅僅使用一條直線來擬和資料，這件模型夠好嗎?

Adding higher order effects

我們求出的直線，將殘值平方和降到了最低，但是問題是房屋的售價是線性嗎?

有沒有可能這是一個2次函數呢?那如果2次是，那個模型是它的最佳擬合?

要確定這件事情其實不難，我們只要重複先前的步驟，並使得殘值平方合最小化即可

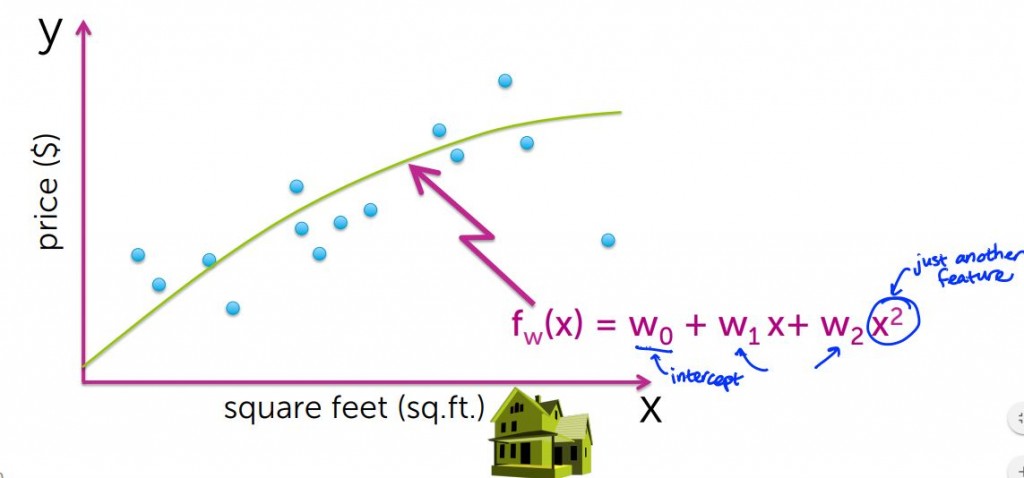
這個2次函數，帶有三個參數w0仍然代表截距，其依可被稱為線性回歸，原因是2次項x平方我們將其視為另一個回歸量

這時候問題來了，如果前面的假設為真，也就是2次函數可以更精準，那我們是否可以無限的增加次方項呢?

現在，過度特化後就會變成這個樣子，在這個結果下殘值平方合幾乎為0，但是試想妳的房子在這個函數裡面最差的情況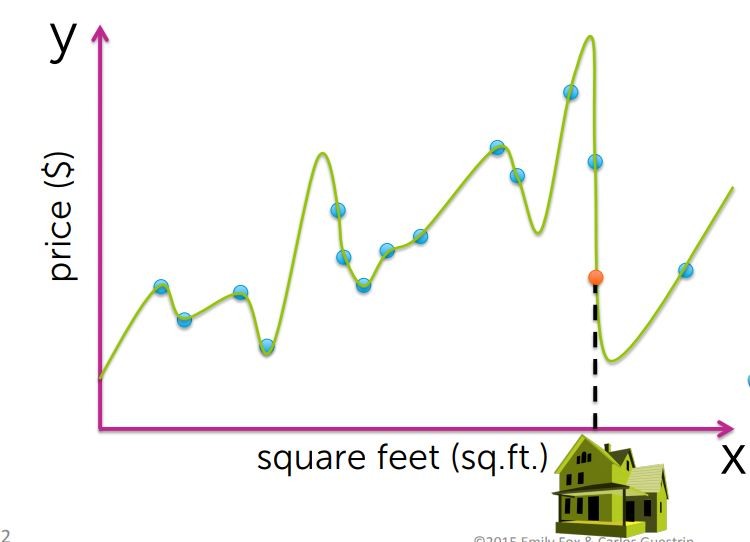

你不覺得這個結果一點都不合理嗎XD

Evaluating overfitting via training/test split

這由13次多項式擬合曲線所引起的問題稱為過度擬合

看到這個也讓我想到一個關於演化的故事，公鹿靠著角來展現其雄風增加求偶能力，照理說鹿角越大的公鹿越能存活下來

但事實上相反，即便鹿角越大的公鹿其越能展現雄風，但是過大的鹿角會降低其奔跑的能力，也就逃不掉食物鏈上層的追殺

我們採用了一個模型並且不段的修正以使其符合我們對事物的實際觀察結果，但這個模型在對新的預測時的一般化能力很差

這個問題其實在任何你想的到的機器學習的模型或統計學模型中是存在的

當我們想擬合一個模型，但我們不希望模型過於侷限在自己的資料集，以至於其一般化能力變差

所以直觀來看，13次多項式確實不合理，而2次多項式確實可以得到更精確的結果

這時候問題來了

我們對於適合的模型階數或模型複雜度問題，該怎樣考慮才是好的?

最好的方法其實是，假設我們可以百分百的預測到未來，那只要透過未來資料回過頭來看，就能知道我們的模型夠不夠好

但是這件事情是不可能的，那退一步來說我們可以做到那些事情呢?

• 從現有資料集隨機排除某些資料，這些被排除的資料，我們稱為測試集
• 將剩下資料用我們設計的模型去擬合，這些剩下的資料，我們稱為訓練集
• 最後將預測的結果跟過去真實的結果比對，最終我們將得知我們模型的準確度

以同樣的方式，假定藍色圈圈是我們的訓練集，我們同樣求出其殘值平方合，這個又稱為訓練損失(Training error)

我們要做的事情是一樣的，就是最小化殘值平方合，找出最小的w-hat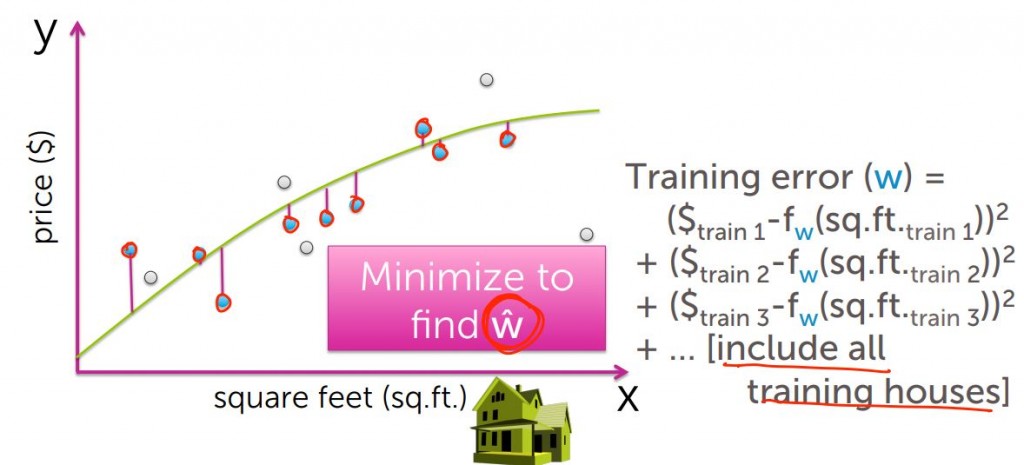

接著用我們的模型來擬合剩下的訓練集，算出其殘值平方合，我們稱為測試損失(Test error)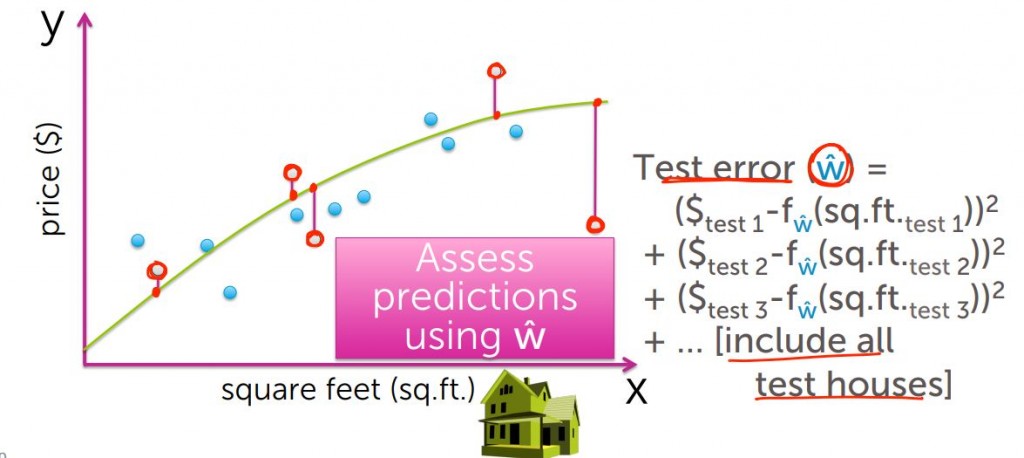

而測試損失和訓練損失是否隨著模型複雜度，呈現某種函數變化關係呢?

由下圖可以看到，從線性到2次甚至13次多項式，我們的訓練損失隨著次方項的上升而不斷的下降

回想一下當我們只著眼於訓練集時最佳化時，產生了什麼樣的問題?

我們得到了一條非常奇怪的線，而可以直觀的想見，這樣子的預測模型將會產生極大的誤差

所以我們可以理解的是，在某一點上我們的測試損失可能會開始上升(公鹿的角大到某種程度時不利於逃過獅子的追殺)

所以測試損失可能下降，但在超過個點之後損失將會重新上升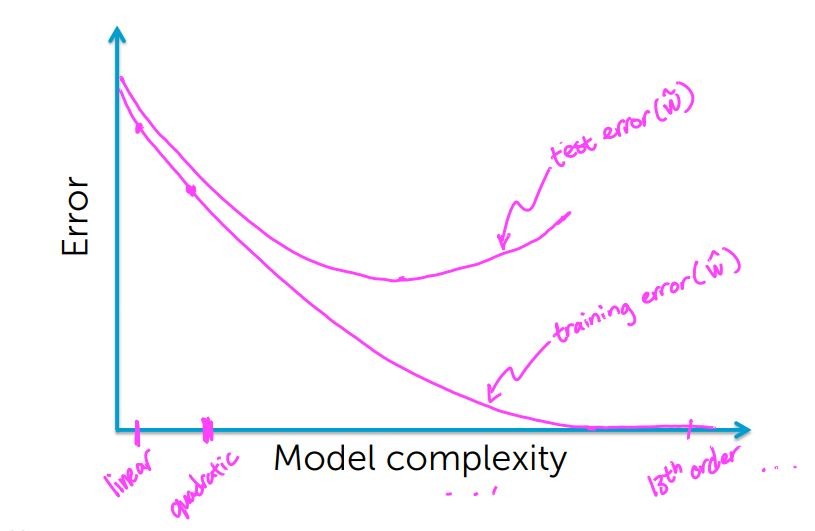

透過這個關係函數所呈現的樣子，我們該如何實際上的正確選擇一個模型呢?

Reference:

• Machine Learning Foundations: A Case Study Approach 華盛頓大學在 coursera 上的公開課程，為本筆記追蹤的主要素材
• 課程投影片