雖然昨天介紹了許多公式，看起來還挺嚇人的，不過實際寫 code 其實並不難實現。加上 python 有好用的 numpy 來簡化向量與矩陣的操作。詳細的實作可以到 github 上查看。

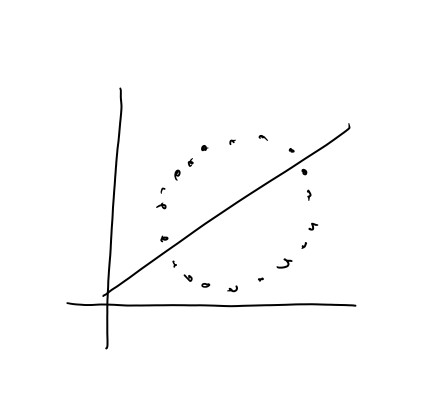
在這次的實驗當中，我們想要觀察的變量為「薪水」，輸入為年份

1. 定義成本函數

2. 線性方程式

3. 梯度下降更新權重

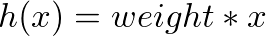
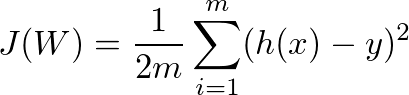
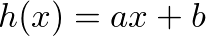
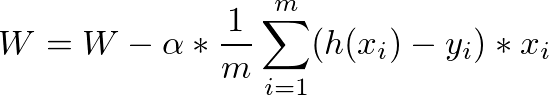
幾乎所有的機器學習與深度學習都在做這幾件事情：

1. 定義 Model
2. 決定成本函數以及誤差
3. 利用梯度下降（也有其他種優化的方式，但梯度下降通常是相對方便且快速的方式，這裡不另外介紹）逐步更新權重
4. 調整超參數（可以根據自己的經驗、需求調整的參數）
5. 注意這邊有個 alpha，在應用上，我們把它叫做學習率（learning rate），之後在介紹梯度下降時會再更詳細解釋一次，這邊可以先把他想像成梯度下降的步伐，如果步伐太快，梯度可能會像鐘擺一樣來回擺盪，導致收斂的速度緩慢，適當地調整學習率可以加速梯度收斂。

現在我們來看看資料：（X軸為年份，Y軸為薪水）

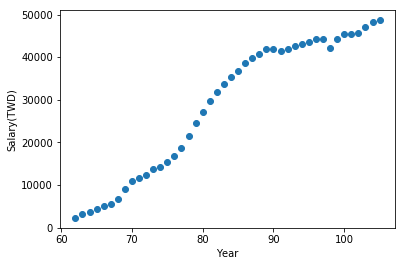
我們現在想要預測的是輸入特定的年份，並且回應對應的薪水。接下來定義一下各種函數

def predict(X, weight):
    return weight * X

def error(X, weights, Y):
    return (predict(X, weights) - Y)**2

def cost(data, weights, Y):
    sum = 0
    m = len(data)
    for i in range(0, m):
        sum += error(data[i], weights, Y[i])
    return (1 / (2*m)) * sum
def gradient(data, weights, Y, alpha, step):
    m = len(data)
    points = []
    for i in range(0, step):
        prediction = data * weights
        errors = prediction - Y

        gradient = (1/m) * alpha * np.sum(errors)
        weights = weights - gradient
        plt.plot(years, data * weights)
        points.append(cost(data, weights, Y))
    return weights

在 gradient 這個 function 當中，我們可以看到 step 這個參數，這個參數決定梯度要下降幾次，如果次數太少，可能還沒有收斂到最小值就迭代完成了，如果次數太多，則有可能梯度已經到達最小值卻仍然在迭代。

現在，來看看我們訓練後的樣子：

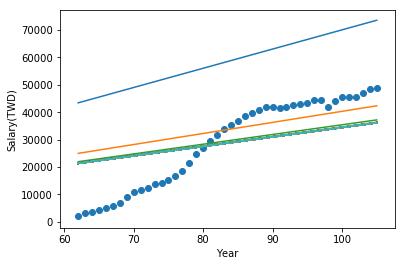
最剛開始的直線（最上面那一條）是把 weight 設為 1 的結果，經過幾次遞迴，直線逐漸往點趨近，最後收斂。

接下來透過訓練好的權重試著預測看看明年的薪水：

print("next year Salary in Taiwan would be: " + "$" + str(w * 107))
print("Salary in Taiwan at 150 would be: " + "$" + str(w * 150))

# next year Salary in Taiwan would be: $49548.5183321
# Salary in Taiwan at 150 would be: $69460.5397179

從這個簡單的模型當中，我們不難發現幾個問題：

1. 感覺訓練出來的結果不夠接近資料的分佈，是因為我只實作了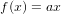 卻沒有加上 b ，因此這條線一定會通過原點。在實務上我們會把 b 也當作一個權重表示。

2. 這個 model 顯然非常不準，只有年份一個變數，但薪水不一定完全是由年份來決定的，可能要看當年的物價指數、整體經濟狀況而定。

3. 如果輸入的資料不是線性的，用線性迴歸的模型來模擬可能就會得到非常糟糕的結果。這時可以透過加入平方項的特徵解決。