Logistic Regression — 邏輯迴歸

前幾天我們介紹了第一個機器學習模型—線性迴歸，線性回歸的目的在於透過歷史資料來預測未來的資料。

而 logistic regression 跟線性迴歸有點不同，我用以下的圖來說明：

如果根據這張圖，很自然地會認為上面的問號應該是 X。

這其實就是邏輯迴歸在做的事情：「根據歷史的資料，當遇見新的資料時，能夠正確判別分類」。不過這一次我們希望輸出的值能夠在 0 ~ 1 之間，來表示這一個資料有多少的機率是 X 還是 O。

所以，我們的 prediction 函數需要修改一下，讓輸出的值可以映射到 0 ~ 1 之間。在實務上常使用的函數叫做 sigmoid function

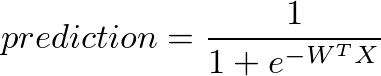
這是他畫出來的圖形：

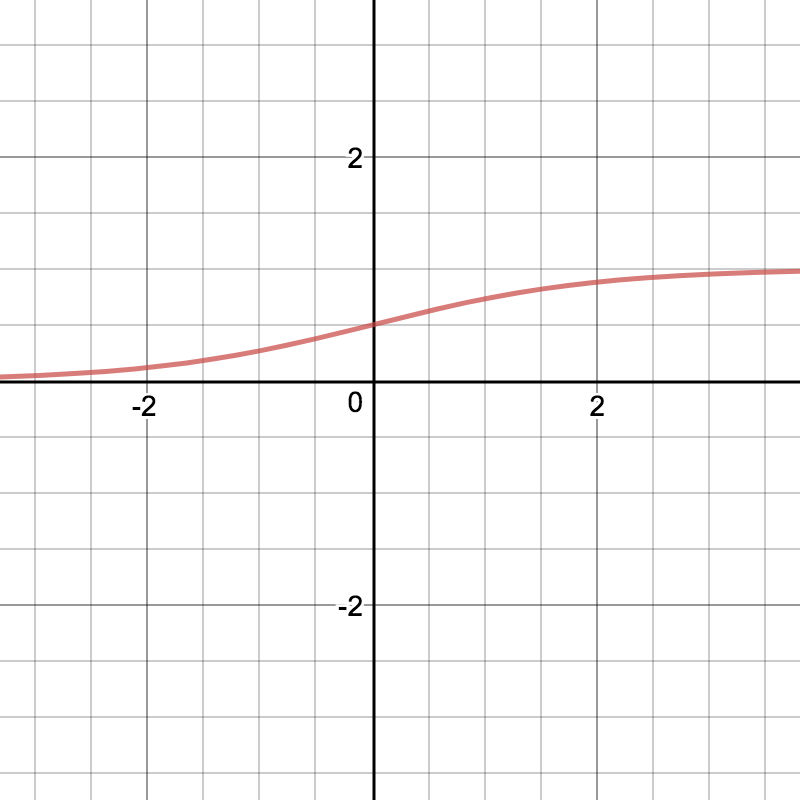
仔細觀察一下這個函數，它有幾個很好的特性：

• 簡單好實作

  def sigmoid(x):
    return 1 / np.exp(-x)
  

• 輸出永遠會在 0 < sigmoid(x) < 1 之間。（注意：不會等於 0 或 1）

• 保有連續性，微分後的長相很單純（下面會推導）

因為輸出的函數已經不再是線性，也就是在線性迴歸使用的最小平方法已經不能滿足需求，需要重新定義一下 cost function。

因為我們的函數已經改為 sigmoid 了，所以可以透過 ln 來定義：

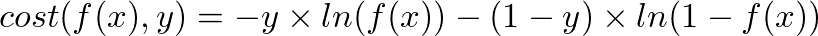
仔細看一下這個函數，我們希望達到幾個目的：

1. 當 f(x) = y 的時候，cost 為 0
2. 當 f(x) != y 的時候，cost 為無限大

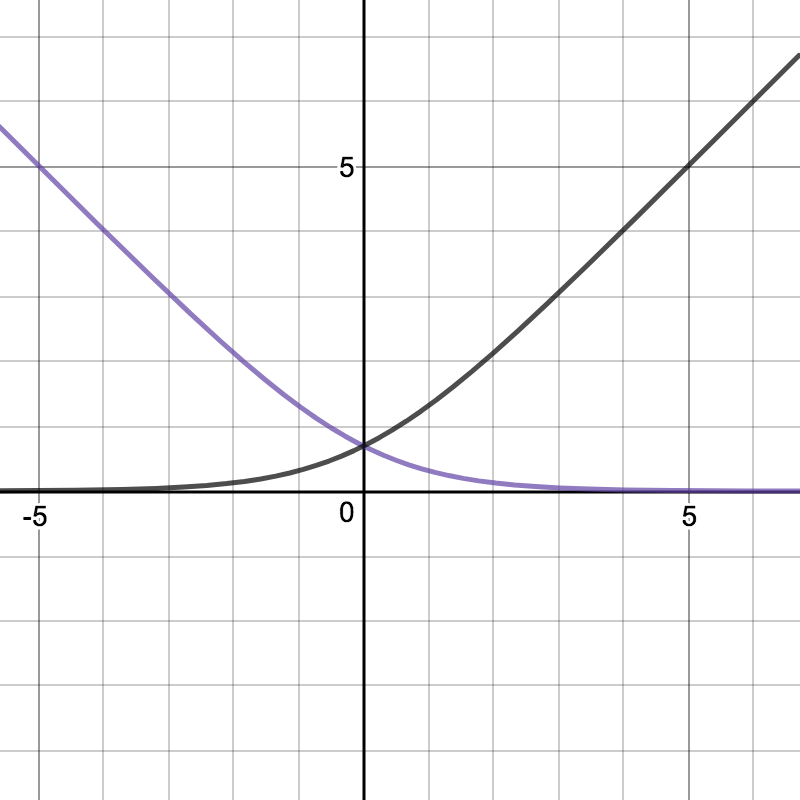
這樣一來，也就更好訓練我們的 model 了。

接下來，我們來推導一下 cost function 的梯度，首先先求算 sigmoid 的導數：

接下來求梯度：

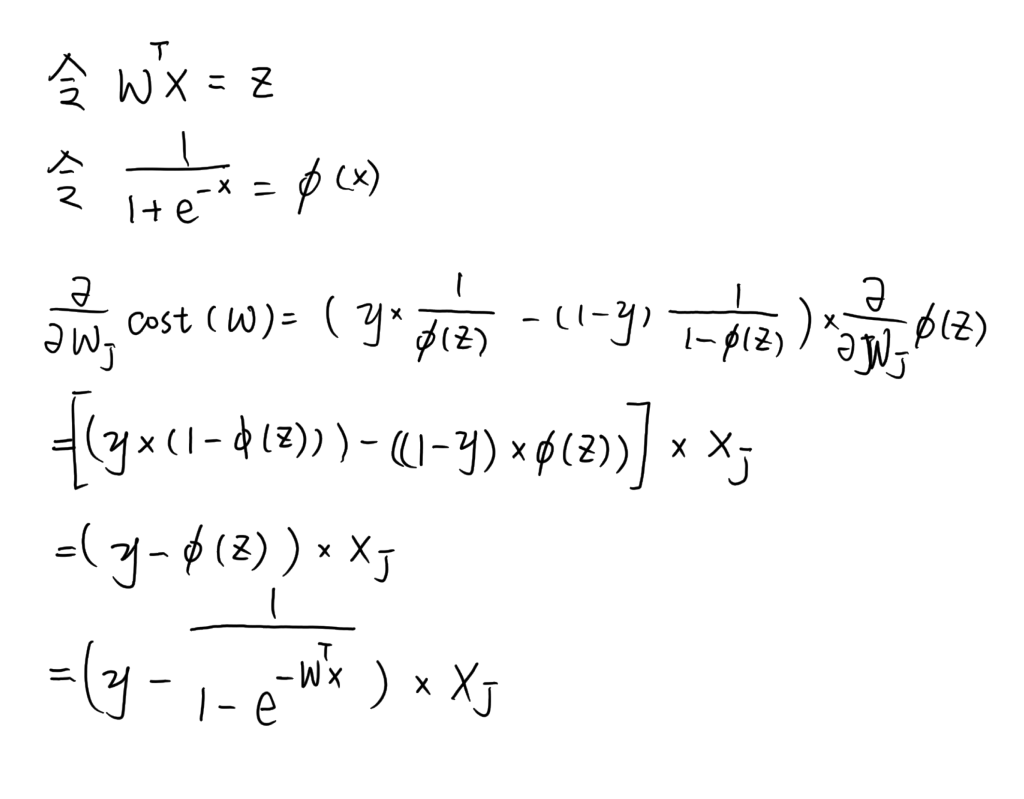
因此梯度下降為：

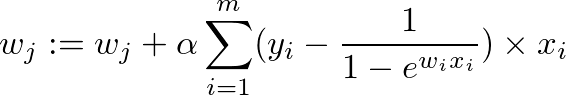
明天我們就來透過邏輯迴歸，試著用薪水與年齡來分類看看是否要發放信用卡吧！