筆記幾乎都來自於O'REILLY Deep Learning。
這次優化筆記講解完,大家也大概了解神經網路的基礎,下一次就要進入到捲積神經網路(CNN)。這次的重點在於Batch Normalization,你也會發現優化方式與上次介紹的範數規一化類似,接下來先介紹如何設定一個比較好的初始化權種方式。
首先先複習上次介紹到的訓練流程。
1.輸入。
2.權重.偏權重(forward)。
3.活化函數(forward)。
4.重複2 ~ 3步驟(依網路深度)。
5.輸出 + 損失函數(forward)。
7.反向進行backward從輸出+損失開始->重複3 ~ 2(backward),權重部分記錄dW和db才能更新權重。
8.訓練權重(使用梯度下降)。
9.重複2 ~ 8步驟(依訓練次數等等)。
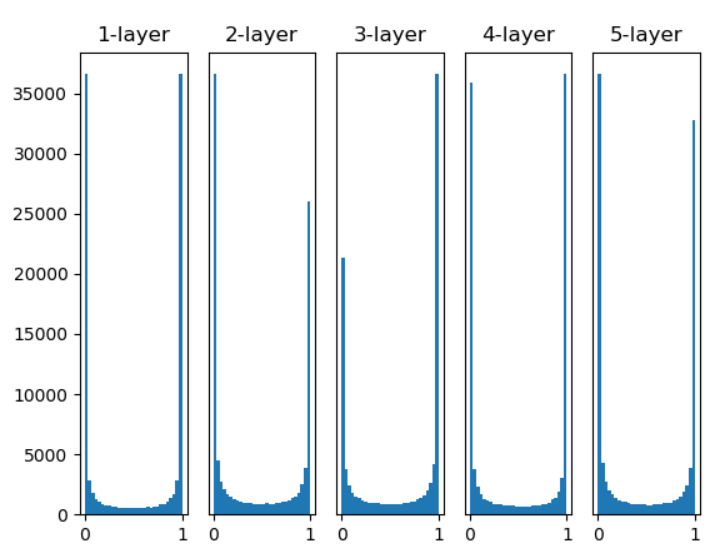
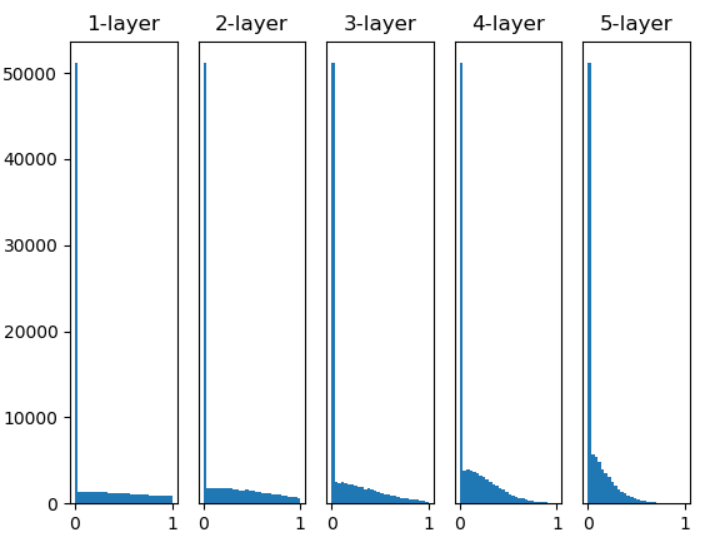
然而在第二個步驟,權重的預設原先都是亂數乘上0.01取得,但這可能會導致"梯度消失"(圖一)或"表現力受限"(每個Layout輸出都類似)(圖二)。
圖一,來源:歐萊里書籍(權重乘上1,活化使用sigmoid)
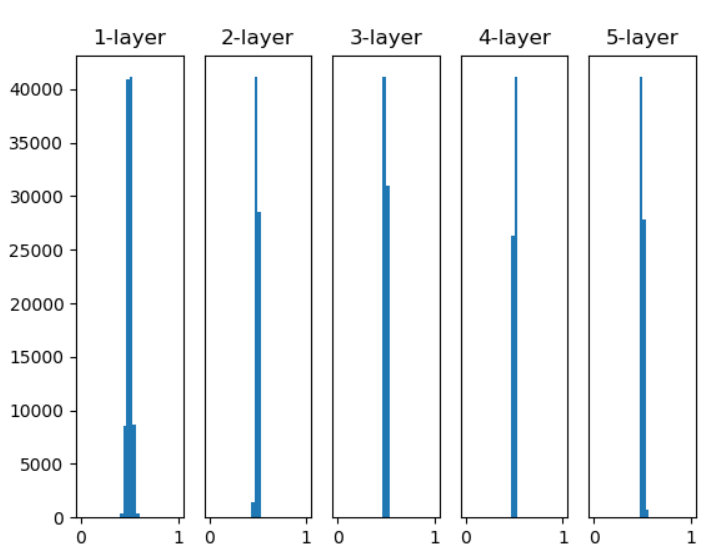
圖二,來源:歐萊里書籍(權重乘上0.01,活化使用sigmoid)
然而Xavier Glorot提出Xavier預設值,Xavier預設為1 / sqrt(n)(圖三),He為sqrt(2 / n),若Relu使用Xavier層數越深就會出現"梯度消失"的情況(圖四)(Relu小於0信息就會消失),所以將其乘上2使數值變大會更加穩定(圖五)。
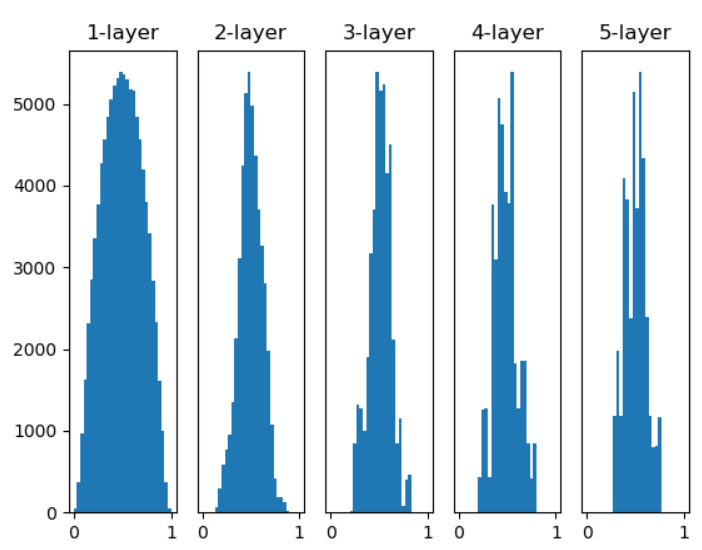
圖三,來源:歐萊里書籍(Xavier預設權重,活化使用sigmoid)
圖四,來源:歐萊里書籍(Xavier預設權重,活化使用Relu)
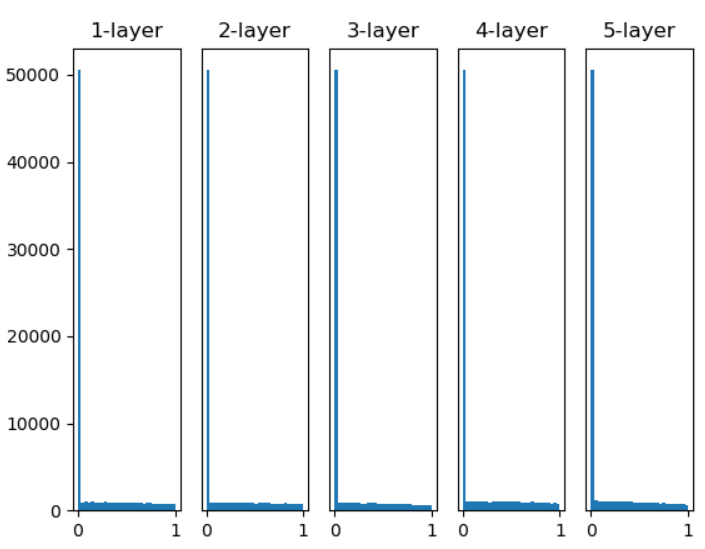
圖五,來源:歐萊里書籍(He預設權重,活化使用Relu)
# 來源歐萊里書籍
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def Relu(x):
return np.maximum(x, 0)
input_data = np.random.randn(1000, 100)
node_num = 100
hidden_layer_size = 5
activations = {}
x = input_data
for i in range(hidden_layer_size):
if i != 0:
x = activations[i - 1]
#w = np.random.randn(node_num, node_num) * 1
#w = np.random.randn(node_num, node_num) * 0.01
w = np.random.randn(node_num, node_num) * np.sqrt(2 / node_num)
#w = np.random.randn(node_num, node_num) * np.sqrt(1 / node_num)
a = np.dot(x, w)
z = Relu(a)
#z = sigmoid(a)
activations[i] = z
for i, a in activations.items():
plt.subplot(1, len(activations), i + 1)
plt.title(str(i + 1) + "-layer")
if i != 0: plt.yticks([], [])
plt.hist(a.flatten(), 30, range = (0, 1))
plt.show()
統計學當中量數分為集中量數和分散量。以下簡單介紹集中和分散的區別。
集中量數:表達目前全部數據趨近的數。
統計中的平均數、眾數、中位數都是屬於集中量數,例如數據[1, 2, 3],它平均值為2,簡單來說全部的數值都趨近於2附近,然而有人會提問3不可以嗎?,這時候就需要使用到分散量數來去比較趨近2還是趨近3,哪一個數是全部數據最趨近的。
分散量數:表達目前數據分散數值(越小越集中)。
統計中的平均差、離均差平方和(變異數)標準差都是屬於分散量數,然而離均差會比平均差比較常使用,因為當數據為極端分數時平均差數據不夠凸顯,如以下例子。
平均差公式: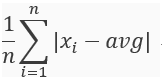 。
。
離均差平方公式: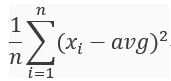 。
。
標準差公式: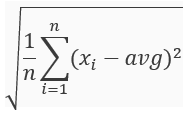 。
。
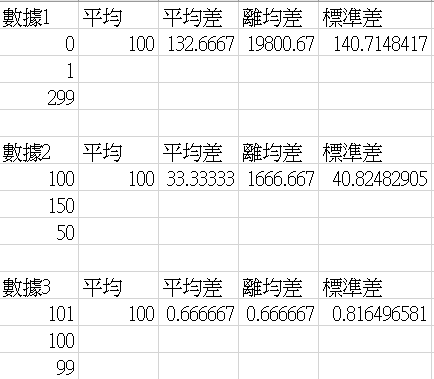
可以看到標準差都會較大,在極端分數值也會比平均差顯得更突出,其實離均差主要是利用面積特性來去取得數值,圖一為平均差計算方式,圖二為標準差計算方式,由圖可以比較平均差像基於一維計算,標準差則是二維平面計算。
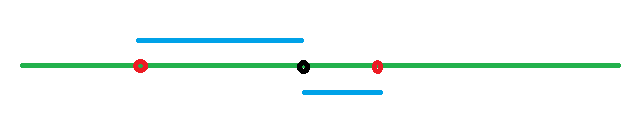
圖一
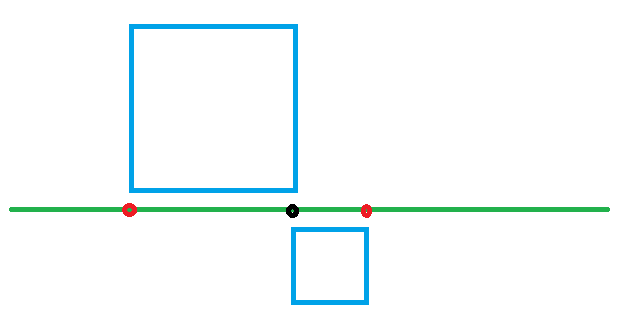
圖二
註:這裡跟範數L2其實有點類似之處,範數L2是計算"整體離散分布",而樣本標準差則是計算"平均的離散分布"。
主要用來將資料規一化,這裡我解釋為利用個數平均差(集中量數)和標準差(分散量數)來計算集中的分布位置,標準差為目前趨近位置,個數平均差則是和平均值的差異和方向(正負),然而取得一個規一化的"標準分布位置",然而這裡多了兩個可以調整參數γ和β,這裡預設為1和0。
公式為,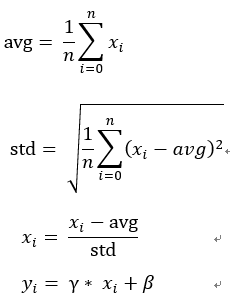 ,接著來分析它的逆向傳播。
,接著來分析它的逆向傳播。
正向傳播:
1.1 / n * sum(x) = avg。
2.x - avg = c。
3.1 / n * sum((x - avg)^2) = var。
4.sqrt(var) = std。
5.c / std = n。
6.γ * n + β = y。
反向傳播,假入傳入的為dy:
1.dβ = dy每行加總(與β陣列大小相同即可)。
2.dγ = dy * n每行加總(與γ陣列大小相同即可)。
3.dn = γ * dy。
// 對應的正向傳播公式。
// γ和β與權重的b一樣在python運算都會自動擴充所以要計算每行加總。
γ * n + β = y
4.dc = dn / std。
5.dstd = -dx * c / (std * std)。帶入除法的反向後每行加總(與std陣列大小相同即可)。
// 對應的正向傳播公式。
// c為每一個數據,std(全部的標準差)與權重的b一樣自動擴充所以要計算每行加總。
c / std
6.dvar = dstd * 0.5 / sqrt(var)。var^(1/2)微分 = 0.5 * var^(-1/2) = 0.5 / sqrt(var)。
// 對應的正向傳播公式。
sqrt(var)
7.原先dc加上 1 / n * 2 * c * dvar 總和(sigma)。直接微分c^2微分 = 2c。
// 對應的正向傳播公式。
// (x - avg)為c所以d(x - avg) = dc。
1 / n * sum((n - avg)^2
8.davg = -1 * dc。減法傳遞。
9.dx = 1 * dc。加法傳遞。
// 對應的正向傳播公式。
x - avg
9.dsum(x) = 1 / n * davg總和(sigma)。與sum(x)陣列大小相同即可。
10.原先dx加丄dsum(x)。
// 對應的正向傳播公式。
1 / n * sum(x) = avg
Batch的反向傳播比較複雜,其中是因為dx和dc要算兩次,因為正向傳播它的公式是分開的,然而最後還要相加在一起,這次多了更號的傳遞和減法的傳遞,所以看起來會相當複雜。
結果虛線為未加入Batch,實線為有加入Batch。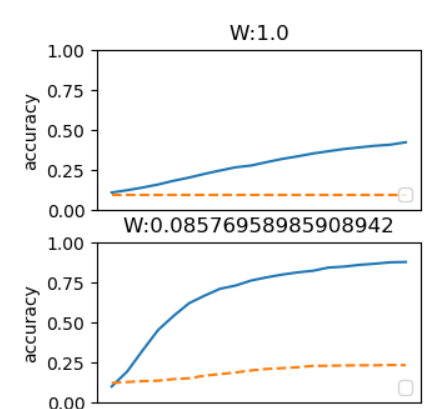
來源歐萊里書籍。
Weight decay(權重衰減)是比Batch出現的更早的,它主要用來過度學習,避免訓練出來的模型只有訓練資料輸出結果是正確的。
通常過度學習都會出現在於權重較大、資料少、訓練次數多都有可能會出現,然而這裡使用L2範數權重衰減,不同地方在於沒有做開更號,可能是因為怕權重會不夠凸顯或是太趨近於0導致無作用。公式為0.5 * lr * W^2每層權重加總道loss結果,lr主要用來控制衰減率,0.5是為了反向傳播更好微分,下面推倒反向傳播公式。
正向傳播:
1.0.5 * lr * W^2。
反向傳播:
0.5 * lr * W^2
1.dW = lr * W。
在原先計算dW時候還要多加上上方的lr * W,範例。
grads['W'] = self.layers['Affine'].dW + self.weight_decay * self.layers['Affine'].W
結果,藍色線條為訓練資料,橘色為預測資料:
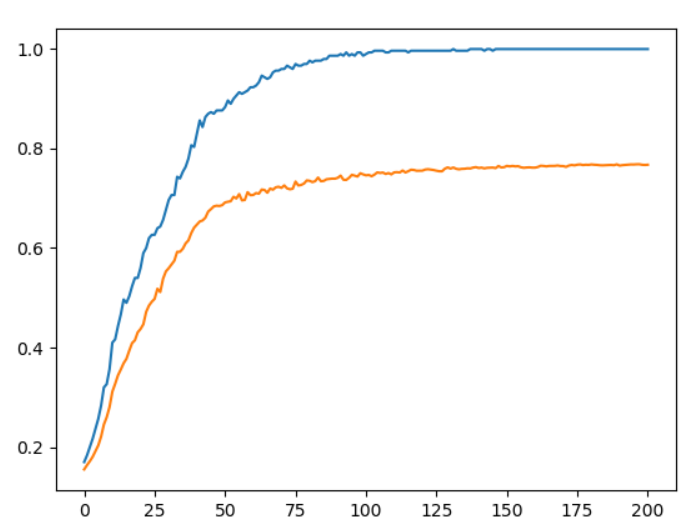
來源:歐萊里書籍(無加入Weight decay)。
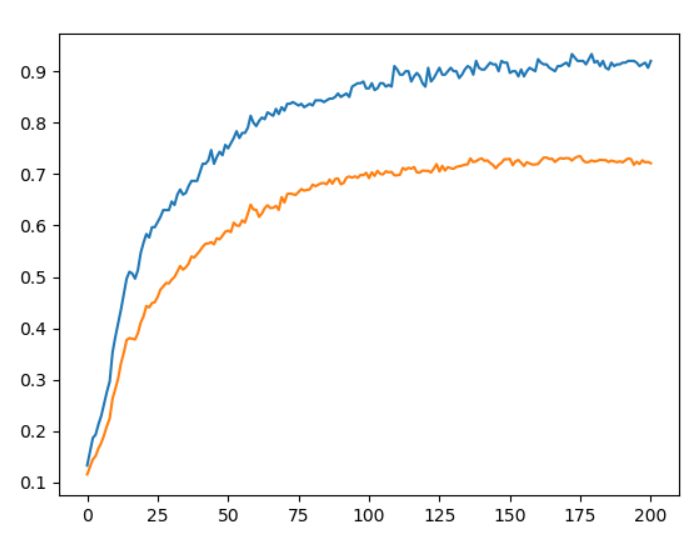
來源:歐萊里書籍(Weight decay = 0.1)。
但在網路較複雜情況下Weight decay的表現效果不一定會很好,因此有Dropout的出現,它實現的的結構我認為更加簡易明瞭。
在目前筆記的神經網路中,過度訓練意思為輸入數據100%可以預測成功,但遇到非輸入資料預測率則會非常低,100%表示已經不會再學習了,所以是若隨機將神經元刪除,依賴性降低(原本只能預測完整的1,現在可能可以預測歪一邊的1),可以預防過度學習到100%,公式,x * (rand(x大小) > drop_base),drop_base為自行設定值,隨機數比drop_base大的設定為1小為0,乘上x後0的將會停止傳遞,以下為推導公式。
正向傳播:
1.x * (rand(x大小) > drop_base)。
反向傳播,假設上層傳來為dy:
x * (rand(x大小) > drop_base)
1.dx = dy * (rand(x大小) > drop_base)。
結果,藍色線條為訓練資料,橘色為預測資料: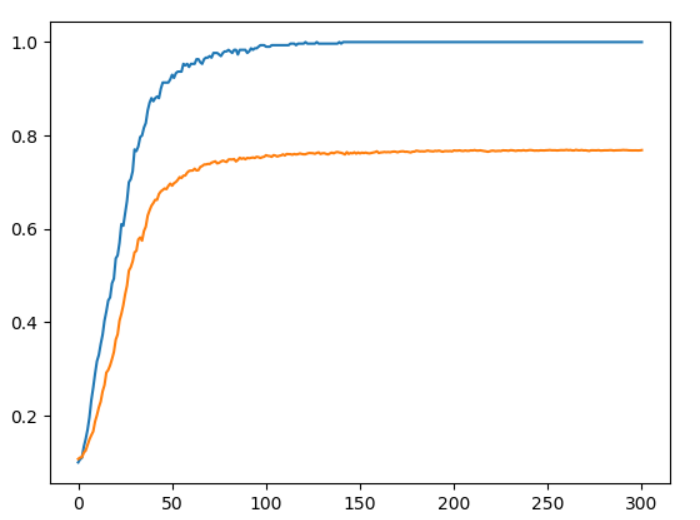
來源:歐萊里書籍(無使用drop_base)。
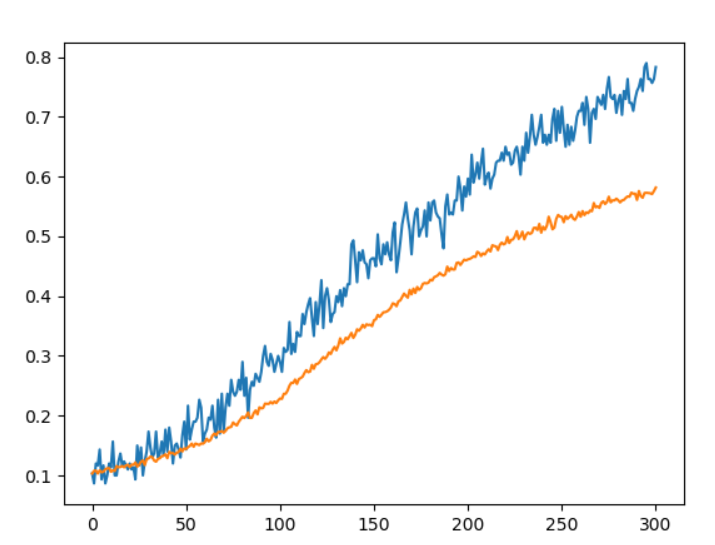
來源:歐萊里書籍(drop_base=0.15,可以調更高但建議深度或廣度要夠)。
神經網路(NN)基礎告一段落,接下來要講解CNN的基礎,雖然CNN不比ResNet來的深和準確,但ResNet也是CNN延伸出來的,當基礎打好能做的東西就會更多。
文章有筆誤或觀念不對的歡迎指導討論。
[1]斎藤康毅、吳嘉芳(譯者)(2017)。Deep Learning:用Python進行深度學習的基礎理論實作。台灣:歐萊禮 。
[2]邱皓政、林碧芳(2017)。統計學原理與應用。台灣:五南出版 。
