Reference: Descending into ML

記得我們昨天說到Machine learning model就是在找feature / label之間的關係，就是從你有的資料(feature)去預測你要的結果(label)，有什麼可以預測的，都可以從你手邊的資料作觀察。

說到觀察，可以看看這次鐵人賽另一個系列的文章: 特徵工程 in 30 days

今天的Google ML一開始提到要預測溫度與蟋蟀叫聲之間"是否"有關係，一開始先把觀測的溫度跟叫聲畫成圖，因為只有兩個數字，所以畫起圖來是很簡單的。

很多時候參數並不是這麼單純，1~2個feacture --> 1個label之間的圖都還很好想像跟觀察，超過以後就不是這麼簡單了

從上圖可以約略看出是我們熟悉的二元一次方程式(一條斜線)，最後會找到一條你model滿意的線(方程式)，並告訴你之後蟋蟀叫幾聲，可能就是溫度幾度。

Learning的過程，大概長下面這樣，橘線是我們的初始值，會慢慢learning到藍色的線: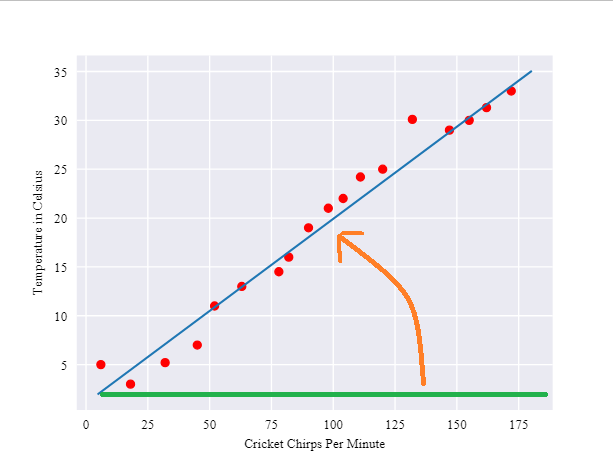

上面一直講到二元一次方程式，我們來硬把他扯上關係。二元一次方程式:

y = mx + b

y: 溫度(要預測的項目)
m: 最後這條線的斜率
x: 蟋蟀叫聲次數
b: y截距(一點偏移量)

OK，這樣就把溫度、蟋蟀叫聲次數跟二元一次方程式湊起來了，剩下b跟m，再讓我們改寫一下: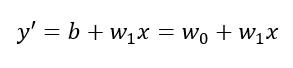

把b換成w0, m換成w1，這兩個參數慢慢調整到train出來的失誤值最小，就是我們要的model了。當然之後可能有w2x2, w3x3, w4x4, 不同的w去調整每個feature x的權重。

當然每次決定一個w0, w1，都會對Labeled examples有loss，所謂Learning，就是把偏差降到最小，像是下圖的橘線到藍線的過程。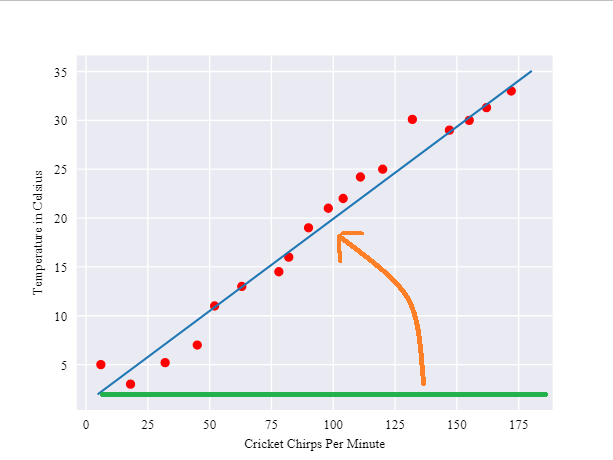

可想而知，下圖中左邊會比右邊的loss還大(因為左圖每個都跟預測的差很遠)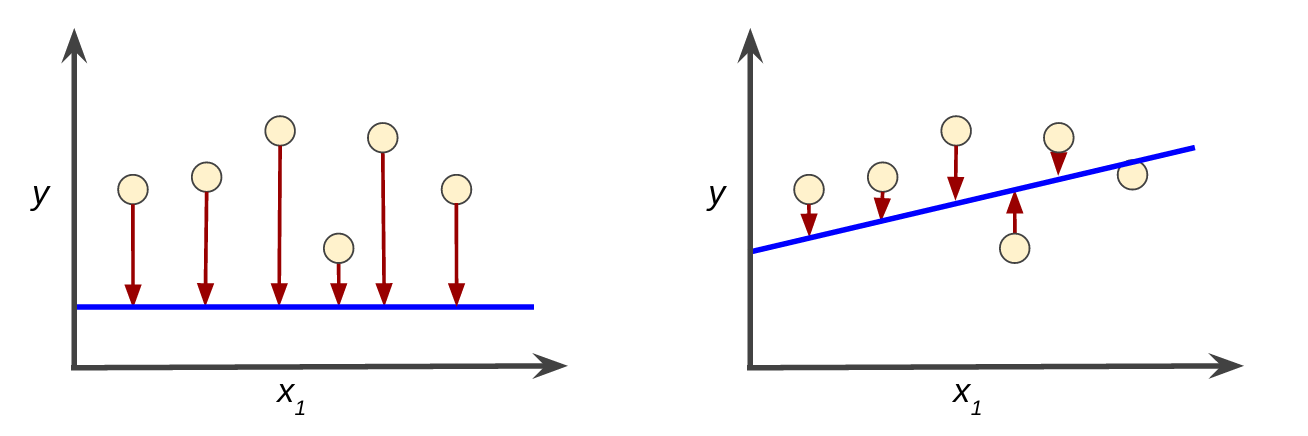

而所謂的Loss的定義，這篇文章介紹了一個Squared loss，又稱L2 loss:

Squared loss
= Label 跟 prediction 相差的平方
= (observation - prediction(x))^2
= (y - y')^2

Mean square error (MSE) 則是把所有dataset裡的squared loss相加後平均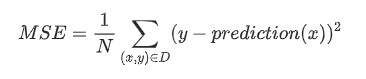

其中
(x, y): 代表每個example中的features x及其對應的label y
prediction(x): 代表權重w與偏移量b對每個x集合算出來的結果
D: 包含(一個、一部、或全部)labeled examples 的 dataset
N: dataset D的數量

不過文末提到一句話，看來之後還有更多 loss function 可以摸喔。

Although MSE is commonly-used in machine learning, it is neither the only practical loss function nor the best loss function for all circumstances.