Ref.: Reducing Loss

An Iterative Approach

一張圖道盡千言萬語:

是不是沒看到結束點？一般來講有steps，或一直到可以接受loss為止(converge)。

記得我們昨天提到的預測函數: 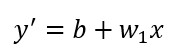，一開始b, w1都喜歡設定成0，之後每個iteration都會去更新它們(每次都會說往前一點、往後一點)。
也因為預設值是0，一般來說第一個預測值y' = 0 + 0*x = 0，若loss function = Squared loss 的話
Squared loss = (y - y')^2 = (y - 0)^2 = y^2。

Gradient Descent

我特別重畫了一下Google的範例，更符合我們定義的w1 = 0的初始值，初始值會得到一個初始的Loss 也是上面說的y^2， 則是代表下一個預測值所需的參數落在的方向及大小。

上圖的Gradient Descent 是把原本的預測函數微分(也就是該點的斜率)，越大就越往前(or往後)一點，越小就往前(or 往後)小一點。也就是說，它包含了方向及大小的資訊在裡面。

Gradient f': prediction function 偏微分 (f')，(loss, weight) 的點在該函數對應的方向有最大的增加量
Gradient * -1 -f': prediction function 偏微分 (f')後乘以-1，(loss, weight) 的點在該函數對應的方向有最大的減少量

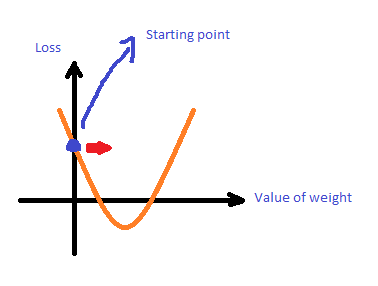
第二步，算出下一個w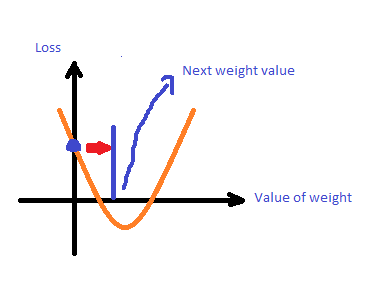

第三步，得到下一個loss

Learning Rate (step size)

要取多少的Learning rate一直是很大的問題，又稱作Hyperparameters，learning rate決定箭頭的長短，下圖中紅色箭頭learning rate小，綠色箭頭learning rate大。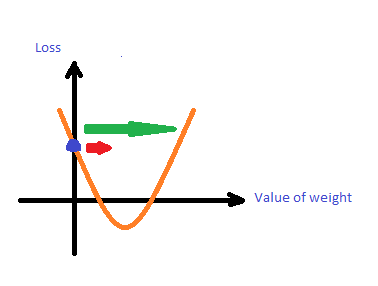

接著就找下一個w，Gradient會帶你去找下一個loss，

w = w - LearningRate * gradient(w)

Optimizing Learning Rate

動手玩一下: https://developers.google.com/machine-learning/crash-course/fitter/graph

Gradient Descent Algorithm

稍微改了最後一個Part，感覺應該是要介紹梯度演算法，梯度演算法有幾種不同的變形，這邊提到了三種

Stochastic Gradient Descent (SDG)

一次挑一個example，但可想而知，如果資料量大的話會跑很久才能train完一個model(跑很多次)。

Batch Gradient Descent

一次把所有examples為進去，這...跑一次可是要跑很久...

Mini-batch stochastic gradient descent (mini-batch SGD)

一次餵少部分的examples去train，平均每個loss算出下一個w。

每個都是Machine learning的大課題，要找初始值、Learning rate、batch-size，大家都盡可能的優化每個步驟，以至於優化整個Learning process。

明天就會進入TensorFlow的世界了，拭目以待吧。