Logistic回歸是尋找最優化算法的方法，主要是利用Sigmoid函式去判斷要被預測的點屬於哪一個分類。
大家應該很熟悉回歸的公式，而該算法是透過把每個feature乘上一個係數，然後把總和帶入Sigmoid中去判斷。
但是要怎麼知道要乘上哪一個係數？要怎麼知道現在用的這個係數就是最佳係數？
因此梯度上升法就是要來處理這個問題。
梯度上升法主張延著梯度的方向去找最佳路徑，找到後每前進一次，梯度的方向會被重新計算，值到迭代的次數到了設定的值，或是誤差已進入可允許的範圍內了。
α是步長，∇f(w)是沿梯度變化的方向，w則是原本的向量，使用步長 * 梯度 更新回歸係數的向量。
梯度上升法：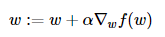
梯度下降的算法跟梯度上升的算法類似，只是把算式中的w+改成w-，來求函數的最小值。
然後因為梯度上升法是用所有的樣本點乘上features去計算然後再加總，這樣做起來似乎會很耗時費力，因此有另外一個方法，「隨機梯度上升法」，來解決這個問題。
隨機梯度上升法是ㄧ次僅採用一個樣本點來判斷。
iThome鐵人賽
看影片追技術