Ref.: Regularization for Sparsity

Regularization在 Day 14時說過L_2 Regularization，再回想一下我們在Day 13 特徵組合的時候，有個很簡單的例子兩種gender、height 3個group，height_x_gneder就有2 * 3 = 6種組合。如果1,000 * 10,000呢？就有10,000,000這麼多種組合，之中又有多少是沒用的feature呢？這種高維度的特徵向量(high-dimensional feature vector)會讓model size很大，而且RAM也會消耗很多。

我們應該減少沒有用的feature，讓他們的weight = 0，以減少RAM的cost。很不巧L_2 Regularization實在沒辦法，只能讓weight變得很小很小，沒用的feature還是會浪費RAM的空間。

聽起來，Regularization term取non-zero的weight的數量，是不是可以讓weight=0的feature沒用？而且model有足夠能力fit data時增加它才合理。這稱作L_0 Regularization，但很可惜這個方法是NP-hard的問題，像是背包問題，很難優化。

還好還有個L_1 Regularization，跟L_0類似，很鼓勵沒訊息的係數設定為0，以減少記憶體使用量。快來比較一下L1 跟 L2吧

L1 vs L2

處罰項目的差異：

• L2 處罰 weight^2
• L1 處罰 |weight|

微分後的意義：

• L2 微分是 2 * weight
• L1 微分後是個常數k(跟weight沒關係)

L2的微分可以想像是刪除x% weight，但zeno芝諾悖論說這種remove x%的方法，永遠不會讓weight為0，只會很接近0。

L1的微分則像是把weight減去某個常數，但因為絕對值得特性，它會在0的時候中斷下來，就是在此時把這個weight zeroed out。

文章下面的Play一定要按看看，可以看到L_1 真的會讓某些weight 停在0，而L_2會跨過去。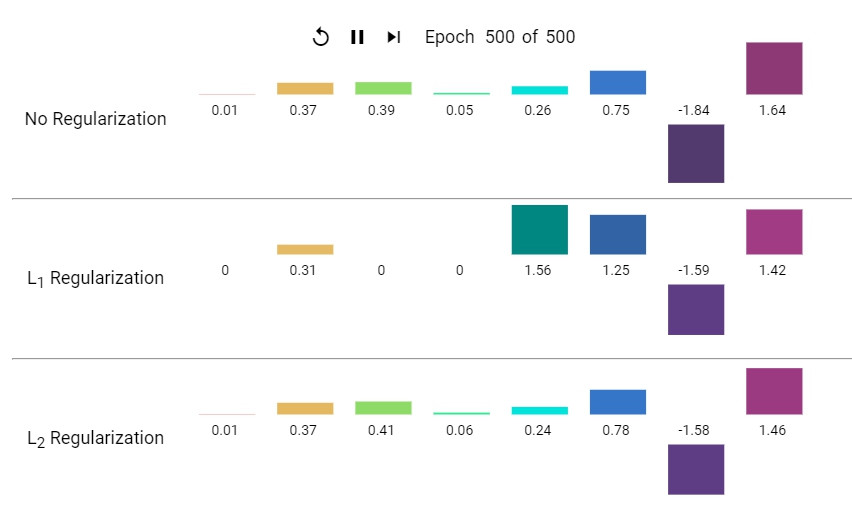

玩看看L1 L2 Playground

這個要注意的是在跑完每個Regularization後的每個weight，L2都不會是0，L1則很放心的讓weight為0

L1 result: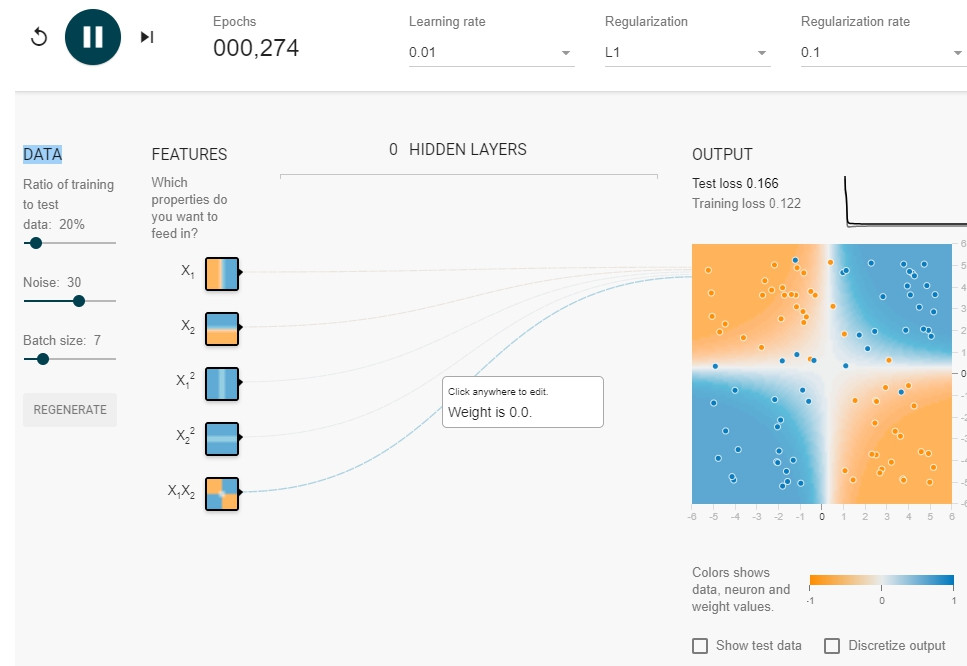

L2 result: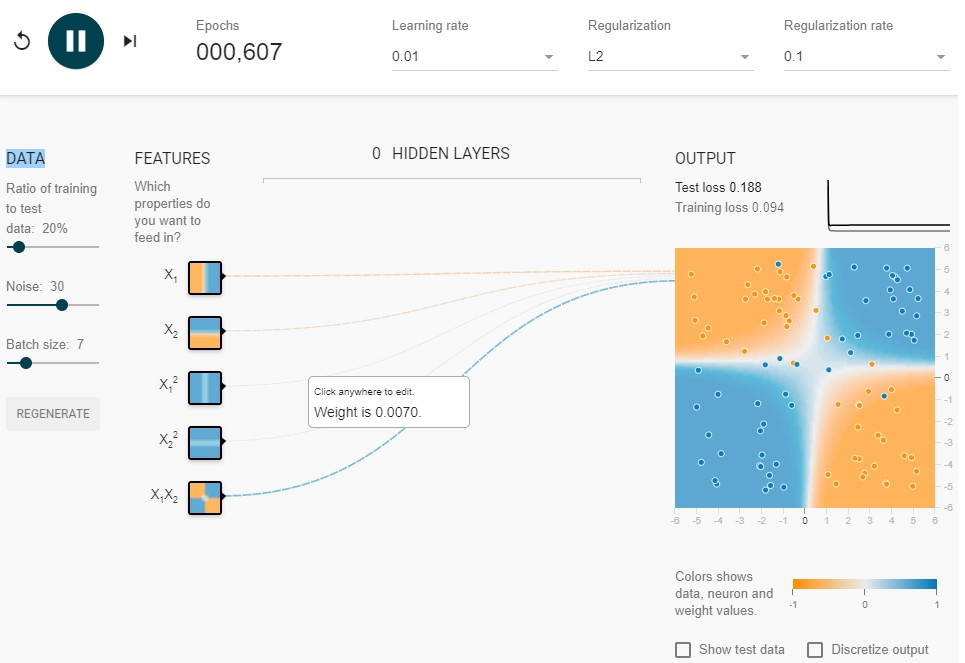

課後練習，看看你對L1, L2 regularization的理解：Check Your Understanding

好囉，今天的就到這邊，明天進入類神經網路了！！