讓我們今天繼續跟向量奮戰吧！

向量的內積

在可以使用乘法而且不會溢位的情況下，我們可以用一次乘法 (摺積，Convolution、又稱捲積) 就把內積的值算出來。但由於摺積的特性，我們必須要把其中一個向量的順序反過來。所以在進行乘法之前，我們得先把向量逐項反過來。

向量反轉

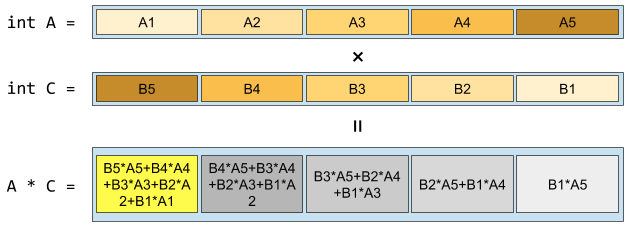
如果向量長度是 k，那麼顯然有個 O(k) 的方法可以逐項反轉。但我們可以利用常見的分而治之(Divide and Conquer) 想法來進行反轉：要反轉 k 個維度，只要先反轉前 k/2 個維度、再反轉後 k/2 個維度、最後將兩個部份的位置交換即可！

如果把這個步驟依照平常的方法寫成程式，那我們會得到遞迴式 ，解出來還是一樣 。 一點都不 Ok 。有沒有辦法可以加速呢？可以的！首先我們假設 k 是個 2 的次方。如果超過的話就把它拆成兩組數字，跟昨天的想法差不多。注意到每一層遞迴的時候，所有遞迴子問題要交換的資料要移動的距離是一樣的！也就是說，在這邊我們可以利用字組的特性在常數時間搞定所有同一層的子問題！

以 為例：

一開始的字組：         01234567
交換最底層的八個子問題： 10325476
交換中間的四個子問題：   32107654
交換最上層的兩個子問題： 76543210

因此時間複雜度就便成了 ，再次心滿意足啦～

小結

今天介紹的技巧被稱為「字組中的平行化」(In-word Parallelism)。我們僅用單一執行緒就可以做到平行處理的概念，用來提升效率。明天我們將看到更多這樣的例子！

對不起今天實在是沒有太多時間可以好好寫稿子――不過我們今天討論的向量反轉和摺積都是很重要的概念唷！之後可能也還會再次遇到～