今天來試試看農場標題XD 在分析某個演算法或資料結構 A 的時候，如果我們能找到另一個相似的資料結構 B 來描述這個資料結構發生的事情，那麼分析效能的方法也可以如法炮製。

伸展樹 Splay Tree

伸展樹是一種二元平衡樹(Binary Search Tree)，其核心操作僅取決於「旋轉」這個操作：

（圖片來源：維基百科 Tree Rotation）

但這個旋轉是有規則的：無論你對這棵伸展樹進行什麼操作，最後存取到的那個節點必須要被以特定規則旋轉至樹根的位置。而我們把這個特定規則的旋轉稱為伸展（Splay）。從 Sleator 與 Tarjan 兩位大師的論文中，我們可以知道依照特定規則伸展後，每一次的操作（插入、搜尋、刪除）就都可以作到 均攤時間。

旋轉的規則依據目前關心的節點 x、它的父節點 p、以及它的祖父節點 g（=p的父節點）的相對位置分成三種情形（Zig、Zig-Zig、Zig-Zag）

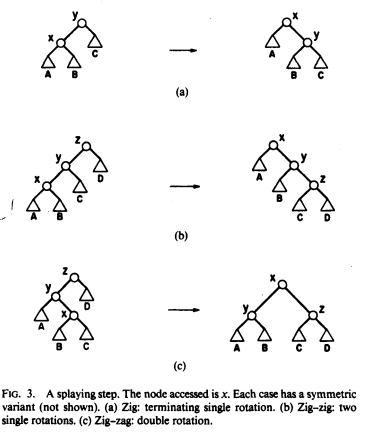
（圖片來源為 Sleator 與 Tarjan 的 Splay Tree 論文）

舉例來說，如果我們有一棵長得很斜的樹：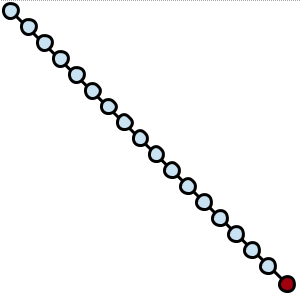

然後存取了最深的節點，接下來，由於這個節點的父節點與祖父節點方位一致，我們可以用 Zig-zig 規則一路將該節點旋轉至樹根的位置，而變成這樣：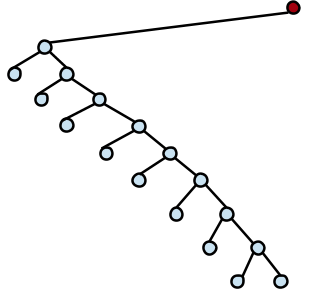

根據一連串精闢地分析，我們可以得出每一個操作的均攤複雜度是 O(log n) 的！

配對堆 Pairing Heap

顧名思義，Pairing Heap 就是一種堆積資料結構（Heap-like Data Structure），廣義的堆積 Heap 是一種保持偏序關係的樹狀資料結構，每一個節點的鍵值都嚴格小於其所有子節點的鍵值（因為是小於，所以習慣上我們會稱它為 Min-Heap）。它可以用來實作優先佇列（Priority Queue）：支援的操作除了插入資料 (Insert)、查看最小值 (GetMin) 與刪除最小值 (ExtractMin) 之外，我們也支援合併兩棵配對堆 (Merge) 的操作。

配對堆就是一種堆積資料結構的實作：

• 合併 (Merge)：假設我們要合併兩個配對堆 T1 和 T2。我們比較一下 T1 和 T2 的樹根大小，比較小的那個當作 root，並且把比較大的那個樹放入 T1 的子樹列表中變成最左邊的子樹。
• 插入 (Insert）：就把新增的資料當成一個只有一個節點的樹，然後呼叫合併。
• 刪除最小值（ExtractMin）：樹根顯然儲存了當前的最小值。把樹根去掉以後，剩下的孩子們要打一架決定誰會是新的樹根。厲害的部份在這裡：假設有 k 個孩子，他們先按照順序由左而右兩兩配對、總共配成 對。把每一對進行合併。接下來，從最右邊開始一路往左，每一次抓最右邊兩顆樹，把他合併。最後就全部合併成一棵樹啦～
  
  （圖片來源為 Fredmen 與 Tarjan 的 Pairing Heap 論文）

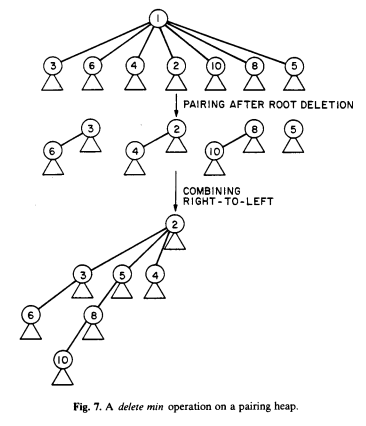
怎麼分析配對堆的效率呢？我們把這個堆疊 T 以「左子樹右兄弟」的方式表示成二元樹 R(T) 的話，上面的 ExtractMin 操作，就相當於對 R(T) 進行伸展樹的「查找最大元素」操作～找完以後的堆疊 T’ 其 R(T’) 形狀與 R(T) 存取完「最大元素」後形狀一樣啊！

於是我們得到的結論就是配對堆的操作複雜度均攤起來也是 O(log n) 的～

後記

我發現左子樹右兄弟(left child right sibling)在日文有很酷炫的名字耶：二重連鎖木。感覺很像某種攻擊力很強的招式之類的XDD

參考資料

Splay Tree https://www.cs.cmu.edu/~sleator/papers/self-adjusting.pdf
https://www.itread01.com/articles/1476714383.html
Pairing Heap https://www.cs.cmu.edu/~sleator/papers/pairing-heaps.pdf