在介紹完了二元樹，今天就來談談二元樹讀取和儲存的方式。二元樹裏的資料其實不一定是依照大小或從左到右排序的，可能依照輸出的方式不同，結果也會不盡相同。

目前理論上有四種輸出順序：

• 前序遍歷 (Preorder Traversal)
• 中序遍歷 (Inorder Traversal)
• 後序遍歷 (Postorder Traversal)
• 層序遍歷 (Level-order Traversal)

但實際上也可歸類為兩種分類方式，深度優先搜尋 (Depth-first Search)、廣度優先搜尋 (Breath-first Search)，只不過節點輸出的順序改變而已。這兩個搜尋會擇日討論。

以下為圖例。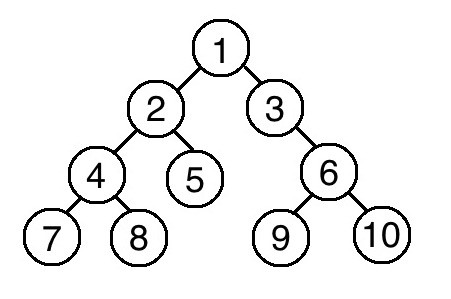

1. 前序遍歷：順序是根節點、左子節點、右子節點，根排在前面。
   [1, 2, 4, 7, 8, 5, 3, 6, 9, 10]
2. 中序遍歷：順序是左子節點、根節點、右子節點，根排在中間。
   [7, 4, 8, 2, 5, 1, 3, 9, 6, 10]
3. 後序遍歷：順序是左子節點、右子節點、根節點，根排在後面。
   [7, 8, 4, 5, 2, 9, 10, 6, 3, 1]
4. 層序遍歷：順序是由根節點一層一層往下，由左往右。
   [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
   　

那如果是搭配四則運算呢？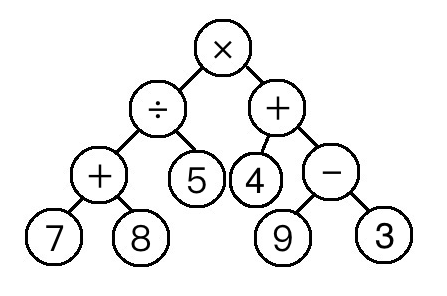

1. 前序 (Prefix)：又稱 波蘭表示法 (Polish notation)。
   [× ÷ + 7 8 5 + 4 - 9 3]
2. 中序 (Infix)：一般的四則運算，須加括號。
   [((7 + 8) ÷ 5) × (4 + 9 - 3)]
3. 後序 (Postfix)：又稱 逆波蘭表示法 (Reverse Polish notation)。
   [7 8 + 5 ÷ 4 9 3 - + ×]

拉蒙碎碎念

有關四則運算的部分，可以自己用程式寫寫看。可以搭配之前說過的堆疊(Stack)來實作喔！