昨天有稍微提過因為 Bellman-Ford 演算法不像 Dijkstra 演算法是用貪心策略找出每個頂點的最短路徑去做擴展,今天就來討論如果 Bellman-Ford 演算法也可以每次僅對最段路徑發生變化的點的相鄰邊,進行鬆弛操作呢?
先上圖。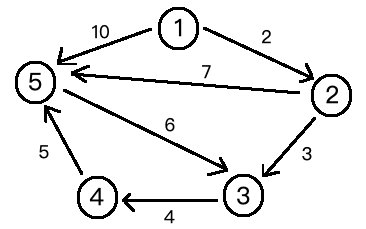
根據昨天執行 n-1 輪 (共有 n 個頂點) 的鬆弛方式,這邊有幾個重點:
上圖邊的資訊。
1 2 2
1 5 10
2 3 3
2 5 7
3 4 4
4 5 5
5 3 6
首先從 1 號頂點開始。1 號加入佇列。
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| dis | 0 | ∞ | ∞ | ∞ | ∞ |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| que | 1 | |||||||||
| 對 1 → 2 進行鬆弛,可以更新,便把 2 加入到佇列。 | ||||||||||
| 1 | 2 | 3 | 4 | 5 | ||||||
| - | - | - | - | - | - | |||||
| dis | 0 | 2 | ∞ | ∞ | ∞ |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| que | 1 | 2 | ||||||||
| 繼續對 1 號頂點剩餘的邊進行鬆弛。 | ||||||||||
| 1 | 2 | 3 | 4 | 5 | ||||||
| - | - | - | - | - | - | |||||
| dis | 0 | 2 | ∞ | ∞ | 10 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| que | 2 | 5 | ||||||||
| 這時將 1 號頂點出佇列 (head +=1 即可,但這邊則將它畫線),並對新佇列首 2 號頂點重複上述動作。 | ||||||||||
| 這邊要注意 2 → 5 的時候,因為 5 號頂點已經在佇列裡,所以不能再次入佇列,但一樣可以進行鬆弛。2 號頂點處離完畢後如下: | ||||||||||
| 1 | 2 | 3 | 4 | 5 | ||||||
| - | - | - | - | - | - | |||||
| dis | 0 | 2 | 5 | ∞ | 9 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| que | 5 | 3 | ||||||||
| 反覆上述的步驟,直到佇列為空。最終結果為: | ||||||||||
| 1 | 2 | 3 | 4 | 5 | ||||||
| - | - | - | - | - | - | |||||
| dis | 0 | 2 | 5 | 9 | 9 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| que |
##全部的程式碼
時間複雜度 O(NM) (最壞情況)
import numpy as np
# 讀入邊
n, m = map(int, input().split(' '))
# 陣列大小要比 m 的最大值 +1
u = np.zeros(m+1, dtype=np.int)
v = np.zeros(m+1, dtype=np.int)
w = np.zeros(m+1, dtype=np.int)
# first 要比 n 的最大值 +1 ; next 要比 m 的最大值 +1
first = np.zeros(n+1, dtype=np.int)
next = np.zeros(m+1, dtype=np.int)
dis = [0] * 7
book = [0] * 7 # 用來記錄哪些頂點已經在佇列中
que = np.zeros(101, dtype=np.int) # 定義一個佇列並初始化
head = 1
tail = 1
inf = 99999999
for i in range(1, n+1):
dis[i] = inf # 初始化 dis 陣列,此處用 1 號頂點到其餘各點的初始路程
book[i] = 0 # 初始化 book 陣列,初始化為 0 ,剛開始都不在佇列中
first[i] = -1 # 初始化 first 陣列下標 1~n 的值為 -1,表示 1~n 頂點暫時都沒有邊
dis[1] = 0 # 從 1 號頂點開始擴展
# 讀入邊
for i in range(1, m+1):
u[i], v[i], w[i] = map(int, input().split(' '))
# 鄰接串列
next[i] = first[u[i]]
first[u[i]] = i
# 1 號頂點入住列
que[tail] = 1
tail += 1
book[1] = 1 # 標記 1 號頂點入住列
# 佇列不為空的時候迴圈
while head < tail :
k = first[que[head]] # 目前需要處理的佇列首頂點
while k != -1 : # 掃描目前頂點的所有邊
if dis[v[k]] > dis[u[k]] + w[k]: # 更新頂點 1 到頂點 v[k] 的路程
dis[v[k]] = dis[u[k]] + w[k]
# 判斷 v[k] 是否在佇列中
if book[v[k]] == 0 : # 0 表示不在佇列中
# 佇列操作
que[tail] = v[k]
tail += 1
book[v[k]] = 1 # 標記頂點 v[k] 已經入佇列
k = next[k]
# 出佇列
book[que[head]] = 0
head += 1
# 輸出 1 號頂點到其餘各點的最短路徑
for i in range(1, n+1):
print(dis[i])
'''
驗證資料:
5 7
1 2 2
1 5 10
2 3 3
2 5 7
3 4 4
4 5 5
5 3 6
'''
本來今天可以偷懶只要打結語的和總表列出來的,但後來想想還是要有始有終,仍舊打了一篇的演算法。
