不論是之前提到過的 Floyd-Warshall 或 Dijkstra 演算法,雖然都很好用也好理解,但卻有一個缺點是無法解決帶有「負權迴路」 (或稱「負權環」) 的圖,因為帶有負權迴路的圖沒有最短路徑。而 Floyd-Warshall 演算法是用多點進行中轉,但如果中轉的過程有負權邊的話,會造成沒有最短路徑,會不斷的繞圈圈。
而 Dijkstra 演算法無法解決帶有負權邊 (邊的權值為負數) 的圖。基於貪心策略,每次鬆弛前會先找到一個最短距離的點變確定值,但如果下次擴展的時候遇到負權的邊會產生更短的路程,有可能破壞已經更新的點路程不會改變的性質。
所以今天介紹的 Bellman-Ford 演算法 便可以完美的解決這件事。在演算法中對邊鬆弛的模式和 Dijkstra 演算法一模一樣,但不同的是不用找出最短距離的確定值,而是用所有頂點的邊的資訊做 n-1 (頂點為 n 個) 輪的鬆弛,這樣就不會像 Dijkstra 演算法中的最短路徑為確定值而無法繼續鬆弛。
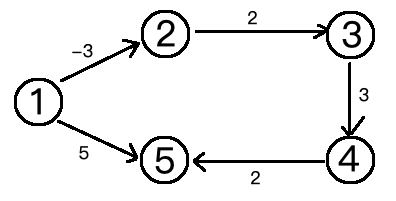
編列出的順序是:
2 3 2
1 2 -3
1 5 5
4 5 2
3 4 3
一樣先用一個 dis 陣列來儲存 1 號頂點到所有頂點的距離,但在還沒鬆弛前,全部設為無窮大。(這邊用 1 號做範例)
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| dis | 0 | ∞ | ∞ | ∞ | ∞ |
現在進行第一輪鬆弛,首先依次讀入邊的資訊進行鬆弛,第一條是 2 3 2: |
|||||
| dis[3] = ∞,dis[2] + 2 = ∞ + 2 = ∞,所以鬆弛失敗。 | |||||
| 1 | 2 | 3 | 4 | 5 | |
| - | - | - | - | - | - |
| dis | 0 | ∞ | ∞ | ∞ | ∞ |
第二條是 1 2 -3 |
|||||
| dis[2] = ∞ > dis[1] + (-3),鬆弛成功。 | |||||
| 1 | 2 | 3 | 4 | 5 | |
| - | - | - | - | - | - |
| dis | 0 | -3 | ∞ | ∞ | ∞ |
| 接至繼續讀入邊的資訊進行鬆弛到結束。第一輪鬆弛完畢。 | |||||
| 1 | 2 | 3 | 4 | 5 | |
| - | - | - | - | - | - |
| dis | 0 | -3 | ∞ | ∞ | 5 |
| 第二輪再從頭開始讀入邊的資訊進行鬆弛,鬆弛完畢的結果: | |||||
| 1 | 2 | 3 | 4 | 5 | |
| - | - | - | - | - | - |
| dis | 0 | -3 | -1 | -2 | 5 |
因為 n 個頂點最多包含 n-1 個邊的路徑,所以最多進行 n-1 輪就行了。
這邊就留給你們想想,真的最多只能包含 n-1 個邊的路徑嗎?最短路徑不可能包含迴路嗎?
答案是:不可能!(hint: 可以分別從正權迴路和負權迴路來想)
但這邊又有一個問題,有沒有可能 n-1 輪的鬆弛太多太浪費資源了?沒錯!這是有可能的。所以我們在每一輪鬆弛前,dis 陣列備份到 bak 陣列中。鬆弛完後再進行比對,如果沒有鬆弛則提前跳出迴圈結束演算法。
另一個想法是,如果在進行 n-1 輪的鬆弛後,仍然可以繼續鬆弛成功的話,那麼此圖就存在負權迴路。因為最短路徑所包含的邊最多為 n-1 條,在 n-1 輪的鬆弛後最短路徑不會再發生變化。如果 n-1 輪鬆弛後最短路徑仍發生變化,則該圖必然存在負權迴路。這也是 Bellman-Ford 演算法可以用來檢測圖是否含有負權迴路。
**時間複雜度 O(NM) ** (其實還可以再進行優化喔)
import numpy as np
n, m = map(int, input().split(' '))
dis = np.zeros(10, dtype=np.int)
bak = np.zeros(10, dtype=np.int)
u = np.zeros(10, dtype=np.int)
v = np.zeros(10, dtype=np.int)
w = np.zeros(10, dtype=np.int)
inf = 99999999
# 讀入邊
for i in range(1, m+1):
u[i], v[i], w[i] = map(int, input().split(' '))
# 初始化 dis 陣列,此處用 1 號頂點到其餘各點的初始路程
for i in range(1, n+1):
dis[i] = inf
dis[1] = 0
# Bellman-Ford Algorithm
for k in range(1, n):
# 將 dis 陣列備份到 bak 陣列中
for i in range(1, n+1):
bak[i] = dis[i]
# 進行一輪鬆弛
for i in range(1, m+1):
if dis[v[i]] > dis[u[i]] + w[i] :
dis[v[i]] = dis[u[i]] + w[i]
# 鬆弛完畢檢測 dis 陣列有無更新
check = 0
for i in range(1, n+1):
if bak[i] != dis[i]:
check = 1
break
# 如果 dis 陣列沒有更新,提前退出演算法迴圈
if check == 0:
break
# 檢測負權迴路
flag = 0
for i in range(1, m+1):
if dis[v[i]] > dis[u[i]] + w[i]:
flag = 1
if flag == 1 :
print("此圖含有負權迴路")
else:
# 輸出最終結果
for i in range(1, n+1):
print(dis[i])
'''
5 5
2 3 2
1 2 -3
1 5 5
4 5 2
3 4 3
'''

感謝樓主! 這篇超級詳細!!!
只是第二輪 結果在文章中是不是有點問題呢?
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| dis | 0 | -3 | -1 | 2 | 5 |
dis[4] 是不是等於2才對? 不是-2。