在還沒有進入多層感知機 MLP之前，Moore請大家注意這一段程式碼， Data Iteration，由於機器學習的數據集通常很大，不太可能一次導進記憶體，所以策略上是要使用一個批量時，再產出 (yield) 給使用需求，訓練器。具體實現如下：

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)  
    for i in range(0, num_examples, batch_size):
        j = nd.array(indices[i: min(i + batch_size, num_examples)])        
        yield features.take(j), labels.take(j) 

重點在資料打亂 (random.shuffle) 產生隨機性，並用 yield 吐出數據。其實在練習機器學習時，無論是用 Tensorflow，還是 Mxnet ，高階的Keras 都有提供訓練資料集的取用 API，我們通常不用花力氣自己製作，但是未來要在真實數據作業，就可能需要撰寫自己的 Data Iteration。

#Tensorflow Kera 提供房價預測線性迴歸的練習用數據 
from tensorflow import keras
boston_housing = keras.datasets.boston_housing

(train_data, train_labels), (test_data, test_labels) = boston_housing.load_data()

二元分類

在線性迴歸大家理解機器學習其中之一的演算法，也能拿其中一個框架 Mxnet Gluon 實作後，Fields 先簡單介紹一下分類問題，因為在現實裡，我們經常是用分類來解決問題，例如：圖像識別，我們可能要分辨照面裡面是否有貓，是二元分類問題。稍微複雜一點的是文字識別，例如車牌識別，我們要將上面的一塊區域轉換成某個英數，這也可以當作是36個圖示分類問題。

我們先從簡單的二元分類問題著手。線性迴歸所用的方程式 這裡出現『T』這個符號是對w做轉置，修正前幾篇文章沒有特別標示我們做的是『矩陣內積』。

現在做二元分類，我們不需要預測值，反過來我們只要預測『是』『否』即可。策略上我們可以轉換成機率，機率超過一個門檻或者說『閾值』我們就猜『是』；反之我們猜否。所以公式變成：

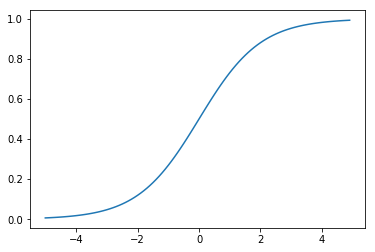
多加了一個稱為 sigmoid function 轉換 ，或者另外一個比較有名的稱號 logistic function。所以有人把這個模型稱為 logistic regression 邏輯迴歸。sigmoid function 表達為：

可以把任何實數轉換為0到1。這個函數我們可以輕易的用python來撰寫，並畫出圖來表達

import mxnet as mx 
from mxnet import nd, autograd, gluon
import matplotlib.pyplot as plt

def logistic(z):
    return 1. / (1. + nd.exp(-z))
    
x = nd.arange(-5, 5, .1)    
y = logistic(x)
plt.plot(x.asnumpy(),y.asnumpy())
plt.show()

分類問題的損失函數 推演：

原來做線性迴歸的損失函數 MSE 亦不可套用在分類問題了，我們推導一下思維，在樣本我們就是要找到一組參數，目標是讓預測的 機率最高，表達為：

已知樣本之間是獨立事件，所以上面的公式就能轉換成：

由於機率不會小於0，取 log 後，還是會得到的同樣的最佳參數參數 ，這樣的目的是為了讓後續 mini-Batch 梯度計算容易。

還記得線性迴歸我們是要最佳化目標是要最小化『損失函數』吧？分類問題也是要損失函數，所以我們加一個 『-』號後，本來是『最大化機率』不就變成『最小化損失函數』：

（公式一）

現在我們用 來表達 第 i 個樣本分類為『是』的機率（）。這樣就可以表達成：

我們可以用更簡潔的方式：

（公式二）

結合上（公式一）與（公式二），我們就可以定義二元分類的損失函數：

結合兩個公式的這個推導還算簡單，就不討論了。能夠定義了損失函數後，後續就剩下取得訓練用的資料集，我們留待明天繼續。

佳麗聽到這裡已經要暈倒："為何我們談的神經網路，到現在都只有數學，我看一堆科普談到AI的文章，常會看到什麼神經元，突觸的。怎麼都沒聽你們講起？"

Pete幫 Fields回答："佳麗姐你如果有受騙的感覺，那我反覺得前人為了行銷這種演算法，把它包裝成類似人腦神經運作似的，這個策略很成功呢！騙了一堆人的關注，有資源了，才會像現在一樣的蓬勃發展"

備註：

專案緣起記錄在 【UP, Scrum 與 AI專案】