前言

在人工智慧當中點對點相乘加上一個偏移值即是一個感知器，今天要介紹兩種基本的預測方法，線性回歸(Linear Regression)和邏輯回歸(Logistic Regression)。而本篇的線性回歸方法也能稱為單層感知器運算。
其實現今人工智慧運用的運算觀念其實都是雷同的，而很多方法的基底都是從這個邏輯所衍生的，所以讓我們從最簡單的實作開始練習。

訓練步驟

1. 輸入x訓練資料。
2. 預測(乘上權重和加上偏權重)。
3. 活化函數(這裡無使用)。
4. 輸出函數(預測數值直接輸入)。
5. 損失函數。
6. 梯度計算。
7. 使用梯度往回修正權重(反向傳播)。
8. 重複2~7。

線性回歸(Linear Regression)

線性回歸在二維當中是用來預測數值，當給予一些資料放入訓練，在二維當中會變為一條線(這裡使用方程式運算)來預測有可能的數值。

程式碼分析

初始化

• train_x為輸入資料，train_y為真實結果，轉為二維資料方便做矩陣運算。
• validation_x為驗證資料，validation_y為實際驗證結果，轉為二維資料方便做矩陣運算。
• input_x為佔符輸入資料，train_y為佔符輸出資料。
• init為initializer類別初始化使用，weights為權重，biases為偏權重。

train_x = np.array([1.,2.,3.,4.,5.,6.,7.,8.,9.,10.,11.]).reshape(-1, 1)
train_y = np.array([1.,2.,3.,4.,5.,6.,8.,9.,10.,15.,16.]).reshape(-1, 1)
validation_x = np.array([1., 2., 6., 7., 11., 8., 10., 12., 20., 21.]).reshape(-1, 1)
validation_y = np.array([1., 2., 6., 8., 12., 9., 11., 17., 25., 26]).reshape(-1, 1)
input_x = tf.placeholder(tf.float32, shape=[None, 1])
input_y = tf.placeholder(tf.float32)
init = tf.constant_initializer(value=np.random.rand())
weights = tf.get_variable(name="weights", shape=[1, 1], initializer=init)
biases = tf.get_variable(name="biases", shape=[1], initializer=init)

預測函數

參數：x為訓練資料，w權重，b偏權重。

• output為矩陣相乘+上偏移結果，線性回歸的輸出函數直接輸出。
• w_hist、b_hist和out_hist為寫入直方圖可視化數據。

def predict(x, w, b):
    output = tf.matmul(x, w) + b
    w_hist = tf.summary.histogram("weightsHistogram", w)
    b_hist = tf.summary.histogram("biasesHistogram", b)
    out_hist = tf.summary.histogram("outputHistogram", output)
    return output

損失函數

使用均方誤差。
參數：y為預測結果，t為實際值。

• pow為計算平方。
• result為計算每列總和後在計算平均，在除二方便微分。(每一列為一筆預測結果，先計算每一列總和可獲得數量，在計算平均即是批量均方誤差)。
• loss_his為寫入scalar值。

def loss(y, t):
    pow = tf.pow(y - t, 2)
    result = tf.reduce_mean(tf.reduce_sum(pow, axis=1)) / 2

    loss_his = tf.summary.scalar("loss", result)

    return result

訓練函數

參數：loss為損失，index為目前訓練次數。

• learning_rate為學習率，使用SGD類別訓練資料，它會自動綁定loss使用tf計算過的公式，並且自動去計算反向傳播(偏微分)。

def train(loss, index):
    return tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=index)

驗證函數

參數：output為預測，t為實際。

• y為計算兩者差異後在計算平均。
• 將驗證錯誤率資料寫入scalar。

def accuracy(output, t):
    y = tf.reduce_mean(tf.cast(tf.abs(output - t), tf.float32))

    tf.summary.scalar("accuracy error", (1.0 - y))

    return y

訓練資料

• 訓練次數為train_times，time為第N次訓練。
• 走訪訓練資料並使用train_op訓練。
• 依照設置train_step數字來決定顯示訓練資料週期。
• 運行summary_op(tf.summary.merge_all())取得畫圖資料。
• summary_writer(tf.summary.FileWriter)加入上述運行結果。
• 使用accuracy_op運算顯示目前誤差率、使用loss_op運算顯示損失率與顯示目前權重。

        for time in range(train_times):
            # train
            for (x, y) in zip(train_x, train_y):
                session.run(train_op, feed_dict={input_x: x.reshape(-1, 1), input_y: y.reshape(-1, 1)})
            
            # access
            if (time + 1) % train_step == 0:
                summary_str = session.run(summary_op, feed_dict={input_x: validation_x, input_y: validation_y})
                summary_writer.add_summary(summary_str, session.run(index))
                print("train times:", time + 1,
                        " accuracy:", session.run(accuracy_op, feed_dict={input_x: validation_x, input_y: validation_y}),
                        " loss:", session.run(loss_op, feed_dict={input_x: validation_x, input_y: validation_y}),
                        " w:", session.run(weights),
                        " b:", session.run(biases))

結果

TensorBoard選擇左邊Trace inputs即可只顯示對當下點選圖有影響的部分，這裡我選擇點選直方圖就能很清楚看到流程，也可自己移出節點，再好點的做法目前想到可用不同Session來去紀錄應該會更清晰。
圖片也可以很清楚看到那些有用到SGD。

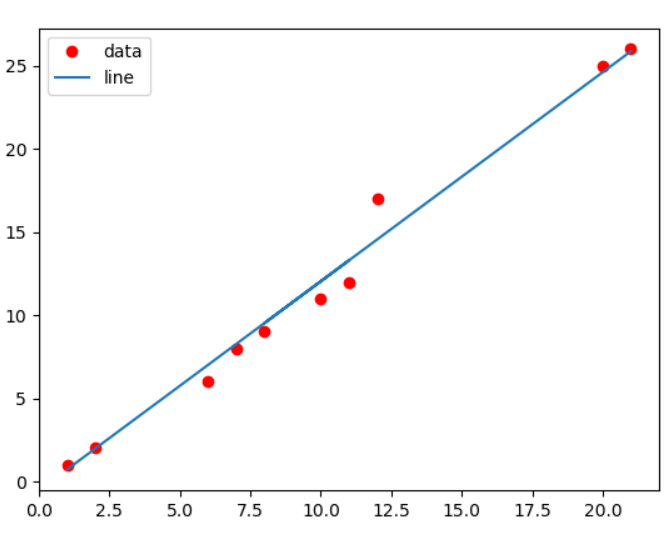
線性回歸結果圖。

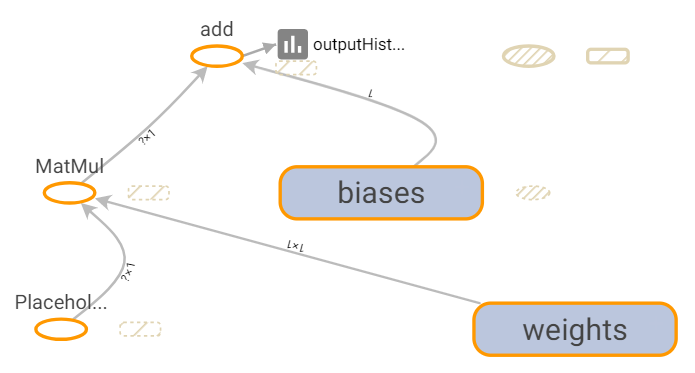
預測函數結果圖。

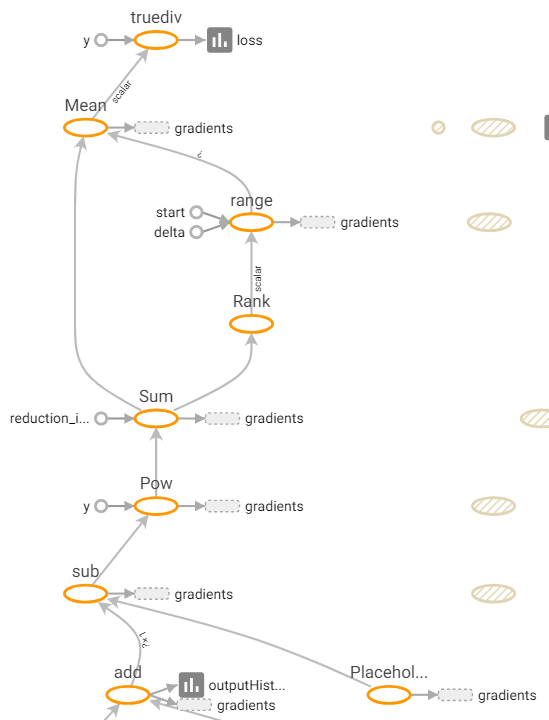
損失函數結果圖。下方add為上方的預測函數。

邏輯回歸(Logistic Regression)

這裡依照書籍直接使用mnist資料，而邏輯回歸則是用來分類，和上述比較其實只相差在於這邊輸出函數使用sotfmax來做規一化，而這裡輸出結果最大者則是此索引對應的數字值。

初始化

• mnist為讀取mnist資料，設置one_hot(假如是3為[0,0,1,0,....])。
• input_x為輸入訓練資料，input_y為訓練結果，784則是mnist每張圖片像素數量。

mnist = input_data.read_data_sets("MNIST/", one_hot=True)
input_x = tf.placeholder(tf.float32, shape=[None, 784], name="input_x")
input_y = tf.placeholder(tf.float32, shape=[None, 10], name="input_y")

預測函數

參數：x為訓練資料。

• weights為權重，biases為偏權重。
• output為矩陣相乘+上偏移結果，邏輯回歸的輸出函數為sofrmax。
• w_hist、b_hist和out_hist為寫入直方圖可視化數據。

def predict(x):
    init = tf.constant_initializer(value=np.random.rand())
    weights = tf.get_variable(name="weights", shape=[784, 10], initializer=init)
    biases = tf.get_variable(name="biases", shape=[10], initializer=init)
    output = tf.nn.softmax(tf.matmul(x, weights) + biases)

    w_hist = tf.summary.histogram("weightsHistogram", weights)
    b_hist = tf.summary.histogram("biasesHistogram", biases)
    out_hist = tf.summary.histogram("outputHistogram", output)

    return output

損失函數

使用交叉熵誤差函數。
參數：y為預測結果，t為實際值。

• cross為計算交叉熵，sum為計算每列總和(每一列為一筆預測結果，先計算每一筆資料的交叉熵)。
• result為計計算平均。(計算平均批量誤差)。
• loss_his為寫入scalar值。

def loss(y, t):
    cross = t * tf.log(y)
    sum = -tf.reduce_sum(cross, axis=1)
    result = tf.reduce_mean(sum)

    loss_his = tf.summary.scalar("loss", result)

    return result

訓練函數

參數：loss為損失，index為目前訓練次數。

• learning_rate為學習率，使用SGD類別訓練資料，它會自動綁定loss使用tf計算過的公式，並且自動去計算反向傳播(偏微分)。

def train(loss, index):
    return tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=index)

驗證函數

參數：output為預測，t為實際。

• comparison為取得目前最大值(索引的對應數字)比較資料是否正確，是輸出1反之輸出0。
• y為計算批量平均誤差。
• 將驗證錯誤率資料寫入scalar。

def accuracy(output, t):
    comparison = tf.equal(tf.argmax(output, 1), tf.argmax(t, 1))
    y = tf.reduce_mean(tf.cast(comparison, tf.float32))

    tf.summary.scalar("accuracy error", (1.0 - y))

    return y

訓練資料

• 訓練次數為train_times，time為第N次訓練。
• avg_loss為記錄訓練資料平均loss。
• batch_size為每次訓練的批量訓練次數，total_batch為計算一次要訓練多少筆。
• 使用mnist.train.next_batch依序取得資料並使用train_op訓練，在計算平均loss。
• 依照設置train_step數字來決定顯示訓練資料週期。
• 運行summary_op(tf.summary.merge_all())取得畫圖資料。
• summary_writer(tf.summary.FileWriter)加入上述運行結果。
• 使用accuracy_op運算顯示目前誤差率。

for time in range(train_times):
    avg_loss = 0.
    total_batch = int(mnist.train.num_examples / batch_size)
    for i in range(total_batch):
        minibatch_x, minibatch_y = mnist.train.next_batch(batch_size)
        session.run(train_op, feed_dict={input_x: minibatch_x, input_y: minibatch_y})
        avg_loss += session.run(loss_op, feed_dict={input_x: minibatch_x, input_y: minibatch_y}) / total_batch

    if (time + 1) % train_step == 0:
        summary_str = session.run(summary_op, feed_dict={input_x: mnist.validation.images, input_y: mnist.validation.labels})
        summary_writer.add_summary(summary_str, session.run(index))
        accuracy = session.run(accuracy_op, feed_dict={input_x: mnist.validation.images, input_y: mnist.validation.labels})
        print("train times:", (time + 1),
                        " avg_loss:", avg_loss,
                        " accuracy:", accuracy)

結果

y = session.run(predict_op, feed_dict={input_x:mnist.validation.images[0].reshape(1, 784)})
print("predict : " + str(np.argmax(y)))
print("really: " + str(np.argmax(mnist.validation.labels[0])))
plt.imshow((mnist.validation.images[0].reshape(28, 28)))
plt.show()

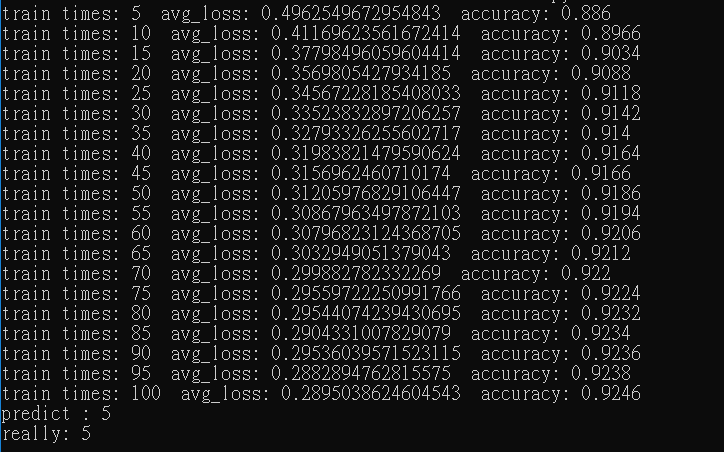
輸出結果。

結語

若之前看過人工智慧文章能發現其實步驟都是很相似的，只是很多地方不用再自己去寫一個類別也不用自己手動算偏微分訓練，而在這樣情況下損失函數就是控制此訓練的主軸了。雖然Tensorflow帶來了許多方便但有很多原理我們還是必須去學習和了解才能加以改良，而文章內容可能有些地方寫的不是很好請見諒，若有問題歡迎留言或私訊謝謝。

參考網址與書籍

[1] https://www.tensorflow.org/api_docs/python/tf
[2] https://github.com/aymericdamien/TensorFlow-Examples
[3] 籃子軒(譯者)（2018）。Deep Learning深度學習基礎｜設計下一代人工智慧演算法。台灣：歐萊禮。