前言

之前發過[筆記]深度學習(Deep Learning)-神經網路學習，而這次讀了[2]這本書發現Adam地方有小錯誤也少了推導公式，而才剛開始讀這本書就能有新的收穫算是一種小確幸。有些部分與書上雷同僅使用文字敘述解說或圖像表示，若有興趣可以去買此書來去探討。

優化梯度下降

梯度下降主要是在計算偏微分(變化)，而當變化最小趨近於0代表為最佳解，但有時候會遇到非全域極小值(駝峰在下的曲線)，或者是鞍點(沒甚麼變化的區域)。而[2]提到雖然計算偏微分可知道當下的方向，但當移動完後，方向又不一定是我們所需要的方向，此時就要在偏微分後的偏微分。在數學公式李海森矩陣可幫助我們判斷極大、極小、鞍點，但計算量是非常大的，因此有人提出優化方式，這次主要介紹Momentum、AdaGrad、RMSProp、Adam這四種優化方法。

Momentum

Momentum顧名思義主要運用動量移動到最底端，例如下圖丟一顆紅球，地心引力往下帶動紅球，到底部時累積的速度可讓紅球往上爬，這時候就有機會擺脫不是全域最佳解狀態，如果使用SGD則到底部時則不再往上爬，這時候可能會導致不是全域最佳解狀態。而這方法稱為指數加權衰減量(依地心引力原理就是計算重力+速度)。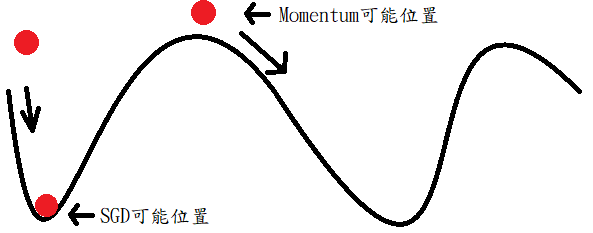

公式

動量更新：
權重更新：
[2]使用不同動量與相對的學習率畫出學習的震盪。這裡參考[2]的點子實作了一次如下圖，可以看到m=0.9時震盪就比m=0好很多，但這裡你應該也會發現這四種的m和學習率相加等於1而1這部分實際上我們並不知道是多少，也就是說可以選擇m=0.9..0.8而總和是N，學習率就是(N-m)，所以到目前為止學習率還是要去猜測的。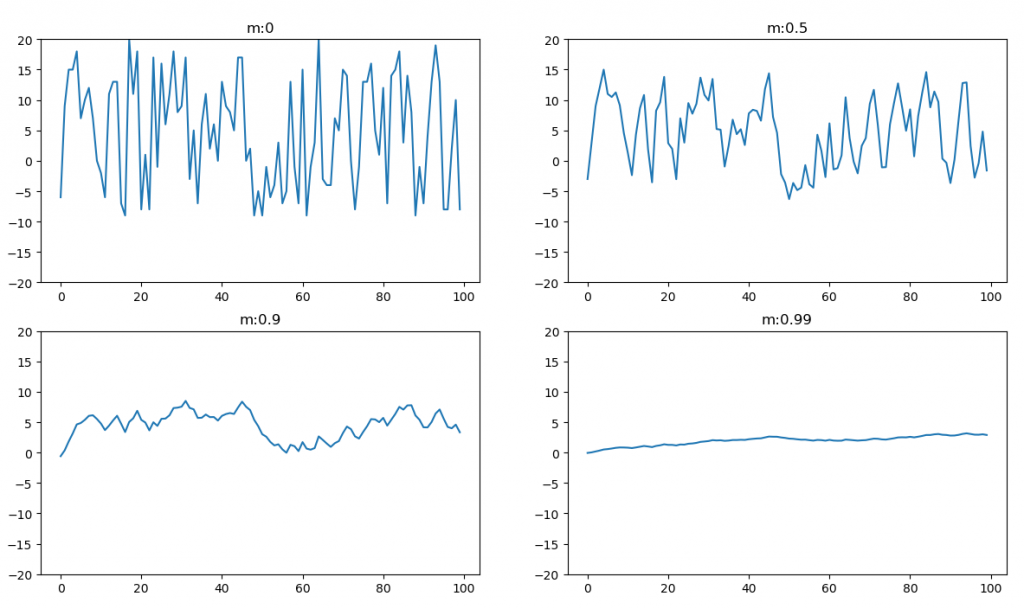

此圖計算動量。

momentum = [0, 0.5, 0.9, 0.99]
stand = np.random.randint(-20, 10, 100)

for index in range(len(momentum)):
    pre = 0
    pre_list = []
    for step in range(100):
        pre = momentum[index] * pre - (1 - momentum[index]) * stand[step]
        pre_list.append(pre)

    plt.subplot(2, 2, index + 1)
    plt.ylim(-20, 20)
    plt.title("m:" + str(momentum[index]))
    plt.plot(np.arange(0, 100, 1), pre_list)

plt.show()

Tensorflow應用

將MLP程式碼的函數train更換。測試後會發現訓練變得較穩定也較快(有時訓練都是7X~8X%，使用momentum迅速提升到9X%)。

def train(loss, index):
    return tf.train.MomentumOptimizer(learning_rate, momentum=0.9).minimize(loss, global_step=index)
    #return tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=index)

AdaGrad

AdaGrad主要利用累積的梯度來去改變學習率，而這裡使用L2範數取得目前累積梯度和。而這裡還會加上一個極小值防止除以0。
註:當然你也可以使用L1範數，但幾乎不會有人推薦使用，因為在人工智慧當中都會盡量使用可微分的公式來表示。

公式

累積梯度:
權重更新:

從下圖可看到隨機數使用越大，學習率也會跟著越大，表示使用AdaGrad學習率就會自動調整。但這時候又遇到一個問題，AdaGrad會隨著梯度調整學習率，所以平坦區域當中若學習率降低到一定程度，會導致無法達到最低點。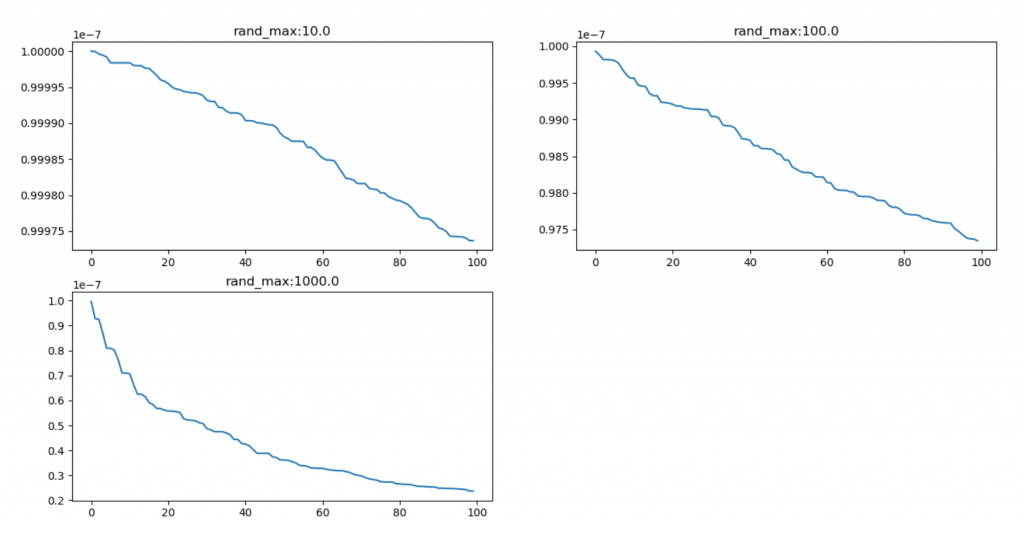

此圖計算學習率。

lr = 1
stand = [
    np.random.randint(0, 10, 100),
    np.random.randint(0, 100, 100),
    np.random.randint(0, 1000, 100)
]

for index in range(len(stand)):
    pre = 0
    pre_list = []
    for step in range(100):
        pre = pre + stand[index][step] * stand[index][step]
        update_lr = lr / (pre + 1e7)
        pre_list.append(update_lr)

    plt.subplot(2, 2, index + 1)
    plt.title("rand_max:" + str(np.math.pow(10, index + 1)))
    plt.plot(np.arange(0, 100, 1), pre_list)

plt.show()

Tensorflow應用

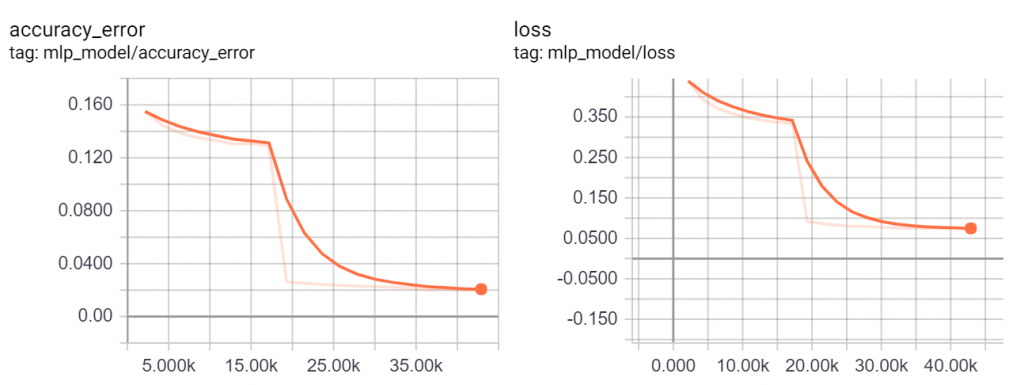
它還有其他參數，但目前無使用到所以它呼叫方式與SGD相同。在SGD訓練8X%時訓練結束很多次都是8X%，但使用AdaGrad它有一瞬間跳到97%準確率如下圖，最後還到了我這幾次訓練都沒看過的98%。驗證了控制學習率是可以讓神經網路更快的收斂。

def train(loss, index):
    return tf.train.AdagradOptimizer(learning_rate).minimize(loss, global_step=index)
    #return tf.train.MomentumOptimizer(learning_rate, momentum=0.9).minimize(loss, global_step=index)
    #return tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=index)

RMSProp

RMSProp是AdaGrad的改善，它加入了指數加權，也能說是AdaGrad和Momentum結合。它與AdaGrad差別在於將歷史梯度的影響變大，減少了訓練時的震盪(Momentum特性)。書中還提到了Nesterow這裡先略過。

公式

累積梯度:
權重更新:

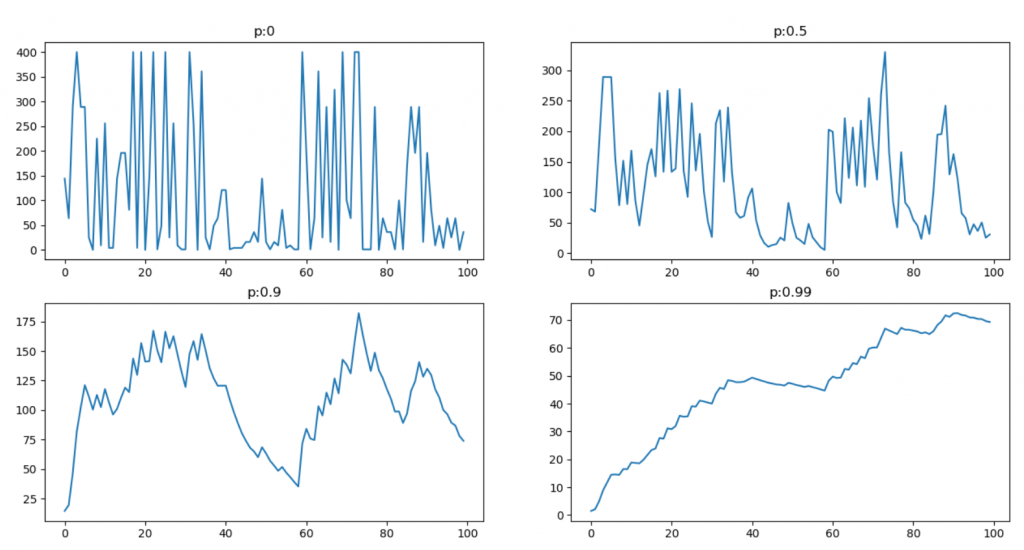
此圖計算動量。

lr = 1
p = [0, 0.5, 0.9, 0.99]
stand = np.random.randint(-20, 10, 100)

for index in range(len(p)):
    pre = 0
    pre_list = []
    for step in range(100):
        pre = p[index] * pre + (1 - p[index]) * stand[step] * stand[step]
        pre_list.append(pre)

    plt.subplot(2, 2, index + 1)
    plt.title("p:" + str(p[index]))
    plt.plot(np.arange(0, 100, 1), pre_list)

plt.show()

Tensorflow應用

這裡decay為衰弱程度，結果如下圖，這裡我只訓練20次(原先100次每5次輸出一次)，可以看到收斂速度非常快，結合了歷史平均梯度的特性並將目前梯度的比重設定為0.1(1-0.9)，既可以利用平均也包含了目前梯度，然而這表示RMSProp的學習率為全域自適應，目前使用它計算感覺是個不錯的選擇。

def train(loss, index):
    return tf.train.RMSPropOptimizer(learning_rate, decay=0.9).minimize(loss, global_step=index)
    #return tf.train.AdagradOptimizer(learning_rate).minimize(loss, global_step=index)
    #return tf.train.MomentumOptimizer(learning_rate, momentum=0.9).minimize(loss, global_step=index)
    #return tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=index)

Adam

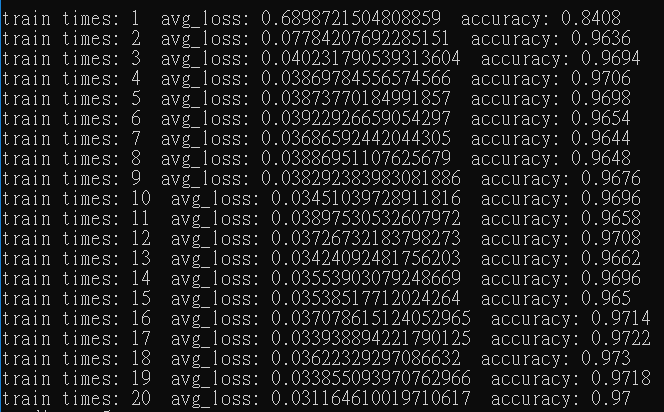
這是本次介紹的最後一種，可以將它看成RMSProp的優化，因為他修正了一開始把p初始化為0的偏差，在前幾次計算權重時都是利用原始的梯度，這裡改用保留歷史梯度的技巧(全域解)來取代原始的梯度。[2]提到所謂的梯度就是第一階矩可表示為，而指數加權則是第二階矩可表示為，差別在於一次方和二次方。(二次方為了計算學習率所以要正規化，因學習率只管梯度大小而不管方向)。

公式

累積目前梯度:
累積梯度:
累積目前梯度修正:
累積梯度修正:
權重更新:

推倒修正公式

[2]使用二階矩來推倒。

1. 展開公式，beta2往前推導，第一項為beta2^目前計算次數-1，第二項為beta2^目前計算次數-2。每多計算一次前面的梯度beta2也會多乘上一次，所以展開才是此公式。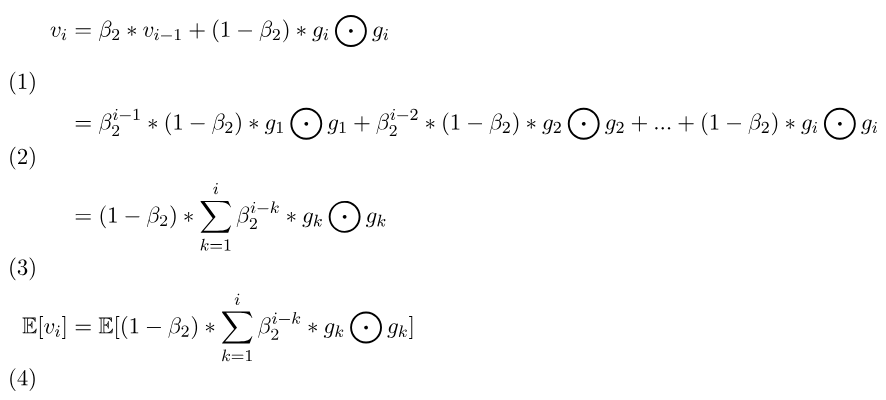
2. 使用sigma代替加總並提出係數(1-beta2)。
   

• 觀點一：使用原先公式可知道v=beta2*舊資料 + (1-beta2)g^2組成，這裡直接假設v=Xg^2，直接帶入上述推導公式，可以將g中的k都取代為i。
• 觀點二：忽略歷史梯度，計算真實的二階矩，這時候帶入上述推導公式，可以將g中的k都取代為i，但beta2還是要留著(雖然我們假設0但留著不影響推倒)。

假設。

3. 將g提到前面。
4. 將sigma展開後，[2]使用代數。
5. 最後除上代數即是修正後的二階矩。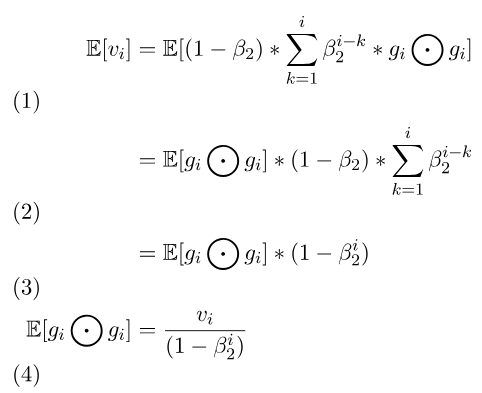
   

而一階矩的推導與二階矩推倒類似，最終結果也是相同的。

Tensorflow應用

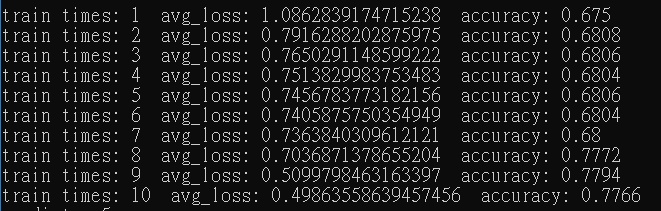
Adam對於不穩定的數據和較複雜的網路有比較好的解，將MLP改為使用5層隱藏層每層200個神經元。若使用上述方法訓練則要調整學習率，且訓練速度並不快(無調整學習率，不到10%正確率)，但使用Adam在這裡則不需要調整，與其他相比收斂速度算快，如下圖訓練十次結果。

def train(loss, index):
    return tf.train.AdamOptimizer(learning_rate, beta1=0.9, beta2=0.999, epsilon=1e-08).minimize(loss, global_step=index)
    #return tf.train.RMSPropOptimizer(learning_rate, decay=0.9).minimize(loss, global_step=index)
    #return tf.train.AdagradOptimizer(learning_rate).minimize(loss, global_step=index)
    #return tf.train.MomentumOptimizer(learning_rate, momentum=0.9).minimize(loss, global_step=index)
    #return tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=index)

結語

現今還有許多人在研究最佳化，而本次只介紹四種最佳化方法，然而未來還會有更多最佳化方式，而最重要的就是要理解或懂得去使用它，若有錯誤或問題歡迎留言或私訊。

參考網址與書籍

[1] https://www.tensorflow.org/api_docs/python/tf
[2] 籃子軒(譯者)（2018）。Deep Learning深度學習基礎｜設計下一代人工智慧演算法。台灣：歐萊禮。
[3] https://upmath.me/