目標：
這題主要目的在於介紹常見的資料結構：樹(Tree)

原題：

Question:
Given two binary trees, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical and the nodes have the same value.

Example 1:
Input:     1         1
          / \       / \
         2   3     2   3
        [1,2,3],   [1,2,3]
Output: true

Example 2:
Input:     1         1
          /           \
         2             2
        [1,2],     [1,null,2]
Output: false

Example 3:
Input:     1         1
          / \       / \
         2   1     1   2
        [1,2,1],   [1,1,2]
Output: false

分析/解題：
給定兩個二元樹，試寫出一個函式來檢查二者是否相等。
(相等的定義是指樹的結構相同，且其相同位置節點的值也相等)

到了第13篇，終於來到樹的部分了，
想當年大學時在演算法的課上被各種資料結構搞得眼花撩亂，
當中二元樹/二元搜尋樹真的只能算小兒科XD
(不信？有心更進階的讀者可以試試看了解一下紅黑樹)

扯遠了，我們回頭來談樹。
在程式的領域中，樹是指資料之間以一種長得像樹的方式連結在一起的資料結構(廢話XD)，以外型而言就像樹狀圖或族譜那樣子，
不過它們有一點比較特別，那就是他們的根通常是畫在上方，下面才是支幹。
如下圖我們所看到的：

1. 每個圈圈我們稱之為節點(node)。
2. 最上面的節點是整棵樹的起始，所以我們就稱之為根(root)。
3. 就如族譜一樣，上面節點是下面直接連接的父母，
   所以我們稱如A是B和C的父節點(parent)(不要問我為什麼不叫母節點XD)，
   而B和C是A的子節點(child)，同時B和C是兄弟節點(siblings)。
4. 任何從自身追尋血脈上去可以到達的節點均為你的祖先(ancestor)。
   比如A是所有人的祖先，而B不是G的祖先。

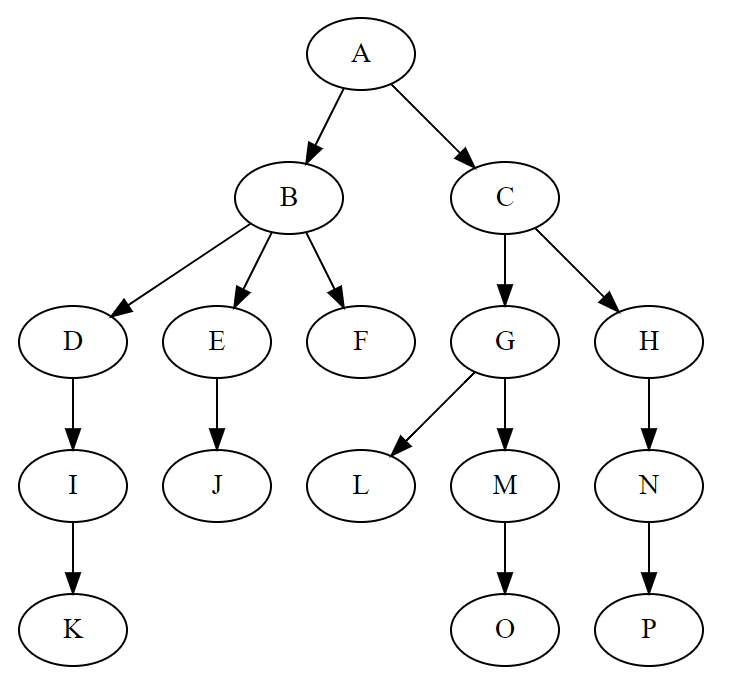
From Wikipedia: Tree

樹本身並沒有規定一個節點要連接多少個節點或總共有多少個節點，
你可以子孫滿堂開枝散葉，也可以孑然一身孤苦伶仃，
只要有一個根在，就可以被稱做一棵樹。

不過這邊要介紹的是二元樹(binary tree)，就有比較明確的限制了，
每個節點最多只能有2個分支。且左右分支是視作不同的，
將它們互相交換的話，前後兩個二元樹會被視為不同的二元樹。
由於只有2個分支，所以一個節點的兩個子節點又可以分別被叫做
左節點和右節點(left/right node)，
單就這兩個節點來看，都可以各自視為一個二元樹，
同樣依照左右被稱作左子樹/右子樹(left/right subtree)。
後續還有一個規範更嚴格，也更常被用到的二元樹稱為二元搜尋樹(Binary Search Tree, BST)，這個我們之後會專門再開一篇講解。
上面這些均為樹的相當基本的部分，並不困難，還請詳加閱讀後再往下。

如同先前提過的linked list一樣，
當一個節點它有一邊沒有連接，或者是已經沒有子節點的時候，
嚴謹的資料結構會將其連接至NIL(表示什麼都沒有)，
而在Java中用null，Python則用None表示。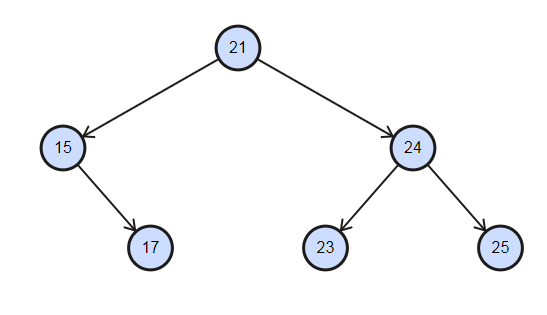

一個Binary Tree, 15的左邊/17, 23, 25的左右其實都是NIL(恩，其實它也是BST)

回到問題，其實問題的輸入是透過array或list的型式，
但這邊LeetCode應該已經妥善處理好建造二元樹的過程了，我們暫且不管它。
我們如何判斷兩個二元樹是否相等呢？
由於相等的前提是結構相同且所有對應的節點的值也相同，
我們勢必要一個一個檢查才能知道結果，
所以我們必須要走訪整棵樹(Tree Traversal)。

一個標準的走訪分成四種模式：
前序、中序、後序以及層序(Pre-order/In-order/Post-order/Level-order)
我們這次只會先從最直覺的前序遍歷開始。

假設如題目所提，我們有兩棵二元樹，他們的root分別是p跟q，
那麼檢查它們是否相等的話，我們要做的事情是：

1. 檢查p和q是否相等
2. 檢查p的左子樹和q的左子樹是否相等
3. 檢查p的右子樹和q的右子樹是否相等
   唯有這三項均成立，我們才能說p跟q兩棵二元樹相等，否則即為不相等。
   接下來，我們先考慮2和3的部分，
   其實就等同於反複拿更小的子樹去做1~3的動作，
   直到比對的兩邊當中有不同或空掉的狀況。

我們拿下面的圖為例，可以簡單推論出，
當檢查兩個節點是否相等的狀況有幾個可確定：
a. 一邊有節點，另一邊沒有節點 => 結構已經不一樣了，所以兩棵樹不同。
b. 兩邊均無節點 => 結構相同且沒有子節點，所以這個位置的子樹相同。
c. 兩邊都有結點 => 檢查值是否相同，相同的話，再檢查左右子樹。
(也就是回到上一段那邊的2~3)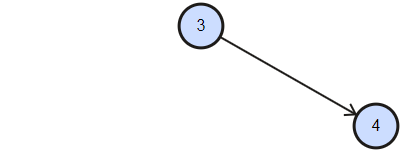

所以，我們可以用連續呼叫自己這個解題函式的方式來解決這個問題，
其演算方式可以大致列成這樣：

isSameTree(p, q) {
    若p和q均為NIL，回傳真
    若p或q為NIL，回傳假(因為表示恰有一個是NIL)
    回傳 (p.val==q.val) 且 isSameTree(p.left, q.left) 且 isSameTree(p.right, q.right)
}

注意這樣子的比較，我們每次是先比較根節點，
再比較左節點的部分，最後才是比較右節點，
同時，每次呼叫isSameTree時，會一路往左邊先找下去，
直到左子樹找完了才會走訪右子樹的部分，所以順序是根-左-右，
也就是一般所謂的前序遍歷(Pre-order Traversal)。

這種不斷呼叫自己來求解的方式，我們稱之為遞迴(Recursion，或譯遞歸)，
這樣的解法一般稱為遞迴解(Recursive solution)。

一般來說還會有另一種解法，
主要是透過額外的資料結構及迴圈，來解決問題，
這種方式叫做迭代法/迭代解(Iterative method/Iterative solution)。
比較熟練的讀者若有興趣，可以自行嘗試使用Queue或Deque來解本題看看。

Java:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null && q == null) return true;
        if (p == null || q == null) return false;
        return ((p.val == q.val) && (isSameTree(p.left, q.left)) && (isSameTree(p.right, q.right)));
    }
}

Python的部分，由於NIL是用None來表示，
所以檢查可以用if not的方法來處理，且not運算的優先層級高於and/or，
所以我們不用額外幫它加括號。

Python:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
        if not p and not q: return True
        if not p or not q: return False
        return p.val == q.val and self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)

面試實際可能會遇到的問題：
「時間複雜度/空間複雜度？」
(如果答案為真的話，那麼每個節點均會走訪一次，故為O(N))
(空間複雜度的話，遞迴同樣會佔用記憶體空間，層數則取決於樹的層數，
如果是平衡樹(balanced tree)的話，因為分布要平衡(填滿)，
每層的節點數量會是1, 2, 4, 8, 16, ..., 總和N=2的n次方-1，n為層數。
所以空間複雜度會是O(logN)，N為節點的總數。
最差的狀況下，節點全部連在同一邊，那空間複雜度可以達到O(N)。)

「可以不用遞迴解嗎？」
(可以，有興趣的讀者可以嘗試看看，具體方式是使用Queue或Deque，
先將兩個根節點放入，接著每次取出一組節點對；
先比較節點，再將兩樹其左右node成對地放入裡面，
重複迴圈，直到有不相等的狀況產生，或直到Queue/Deque內再無節點。)

從LeetCode學演算法，我們下次見囉，掰~

下篇預告：
0101. Symmetric Tree (Easy)