今天的學習模型優化的目標有:
我們將會依序介紹到:
考慮一個簡單的線性模型如下圖示,y=b+Xw,其中X是輸入的特徵(input features),y是模型的預測值(output prediction),b和w都是模型要學習的參數(model parameters)。

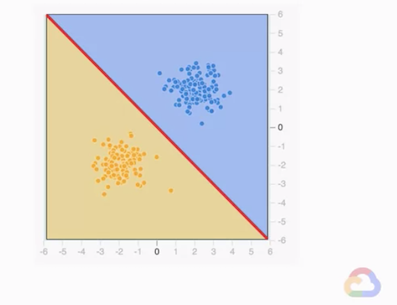
若在一個分類問題上,如下圖,我們就是要找出一個決策邊界(Decision boundary) 來將2類不同的資料分開來,更具體的說就是要找出b+Xw=y,y大於某個值就是A類,小於某個值就是B類。
若考慮現實的一個問題:如何在嬰兒出生前預測他的健康?下列3個特徵哪個適合當作模型的輸入?
顯而易見的,第2、3項都是在嬰兒出生後才能得知的訊息,但這並不符合實際的應用場景,所以第1項媽媽的年紀才是適合的輸入特徵。
若我們拿美國政府的資料來做散佈圖(Scattering plot),媽媽年紀對嬰兒重量如下圖,這邊要注意到一個實作上的關鍵重點,在畫大量資料的散佈圖時,我們會使用取樣的資料(sample data),而不是所有的資料,這是因為將所有的資料畫在圖上,當資料量過大時是不可行且難以呈現具代表性的東西。
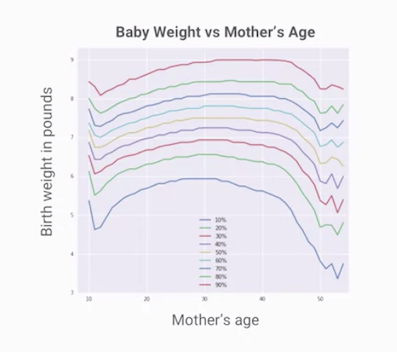
進一步畫出百分位數圖如下,我們可以看出更有意義的資訊:當母親年齡大約落在30歲時,嬰兒的體重會比較高,年齡往兩端反而嬰兒體重會往下。
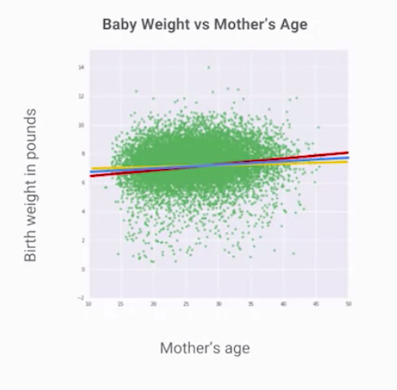
此時我們建立一個線性迴歸模型來擬合資料,可以發現很多條線看起來都好像都差不多,當然,如果有學過統計的人就會知道這種線性模型,如昨天文章提到的,若使用最小方差(Least mean square error)都有對應的解析解,然而當資料量太大的時候,計算解析解的方法便不可行了,因此在ML模型優化的時候多使用到梯度下降的方式,而使用梯度下降前,我們便需要先定義損失函數!
損失函數是用來評估模型不同參數之間的好壞,當損失函數的值越大的時候,代表越不接近真正的答案或標籤,表現就越差,這邊介紹2個常用的損失函數:
RMSE:用在迴歸模型
Cross-entropy error:用在分類模型
有了評估模型參數好壞的損失函數後,我們要怎麼去尋找適當的模型參數呢(優化模型)?答案就是使用梯度下降。
若把損失函數對模型參數做圖,我們可以得到損失函數的曲線,下圖為損失函數的等高線圖(contour),圖中黑點移動的路徑是朝著損失函數最小的地方移動。
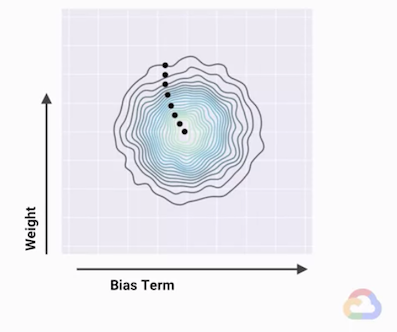
尋找最低點(minimum) 的過程自然就有兩個問題:要往哪個方向?要走多大的步伐?當步伐固定時,走的太小步會讓模型收斂到最低點所需的時間太久,走得太大又會導致模型無法收斂。
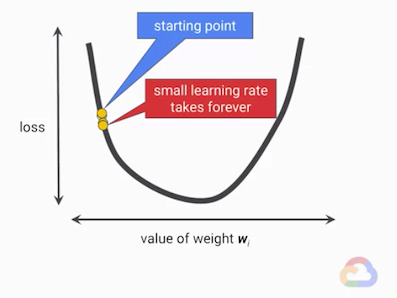
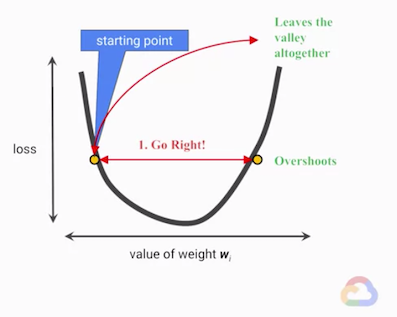
而固定步伐大小還有一個問題,隨著模型參數的學習、改變,很難選到一個適當的大小適用於全部的訓練過程。

因此就有人想到,若在訓練過程時,步伐大小是依據損失函數的微分(derivative)值,在斜率大的地方走大步一些,斜率小的地方代表快要接近極值發生的地方,就走得慢一點,這就是梯度下降的概念。

在實際訓練的時候,我們會把訓練過程中,損失函數值的變化做圖出來觀察模型的收斂,若像下圖發生來回震盪或是很平整的情況,這時候就需要調整超參數(Hyperparameter):學習率(Learning rate),它也是影響學習時步伐大小的一個參數,一個理想的模型訓練過程是,損失函數隨著訓練次數越來越低,才是正確又穩定地往收斂的點前進。

另外有的人可能會問說,為什麼我的模型每次重新訓練得到的值都不同呢?答案很簡單,通常損失函數是一個高維度的平面(隨著參數的維度增高自然增高),所以會有很多次低點(subminimal points) 如下圖右,因此當你的出發位置不同的時候,模型有可能收斂到的最低點只是離他出發最近的次低點。

在訓練的過程中,為了加快收斂速度和減少計算量,還會使用如小批次的訓練(mini-batch training),一般選擇一個批次約10~1000個資料,這樣一次只需要計算這些點的微分(計算微分的值是很耗費運算資源的)來更新模型參數就可以了。
另外雖然我們會檢查損失函數的變化,但不會每更新一次參數就檢查一次,通常會讓檢查的頻率少一些,因為要計算當前的損失函數也需要額外耗費計算資源。
若想要玩看看簡單的模型訓練過程可以到這裡:https://playground.tensorflow.org/
表現衡量可以讓我們量測什麼是重要的,其特點有:
最常用的就是混淆矩陣了,這部分在Day4的文章有詳細的介紹,這邊就不再贅述了。
今天介紹了模型優化的重要概念,明天我們將介紹什麼是 “泛化和取樣”。
