解決不了人的話還是乖乖解決問題吧！填表方法是實作動態規劃演算法的一種方案，而有趣的是，大部分的動態規劃問題也都可以用填表方法來解決。只要找出正確的填表順序即可！

Example 3: Leetcode 62 - Unique Paths

題目連結

https://leetcode.com/problems/unique-paths/

題目敘述

有一個機器人站在 方格的左上角，他想要每一次往右或往下走一格，最終走到最右下角的走法有幾種？

解題思考

不妨定義左上角的格子座標為 (0, 0)、右下角是 (m-1, n-1)。如果現在機器人走到了 (row, col) 的位置，那麼它到達該位置的前一步很可能是從 (row-1, col) 或是 (row, col-1) 走過來的。因為最後一步走法不同，所以我們可以利用加法原理將「走到 (row-1, col) 位置的方法數」與「走到 (row, col-1) 位置的方法數」加起來，得到「走到 (row, col) 位置的方法數」。

參考程式碼(python)

class Solution:
    def uniquePaths(self, m: int, n: int) -> int:
        # 先開一個 m*n 的大表格，並讓邊界的預設值為 1（代表有一種走法）。
        dp = [[1] * n for _ in range(m)]
        for row in range(1, m):
            for col in range(1, n):
                dp[row][col] = dp[row-1][col] + dp[row][col-1]
        return dp[m-1][n-1]

如果我們將每一格代表的子問題「走到 (x, y) 位置的方法數」，所依賴的格子以箭頭方向畫出，不難發現以下三種填表法都可以正確計算出答案：

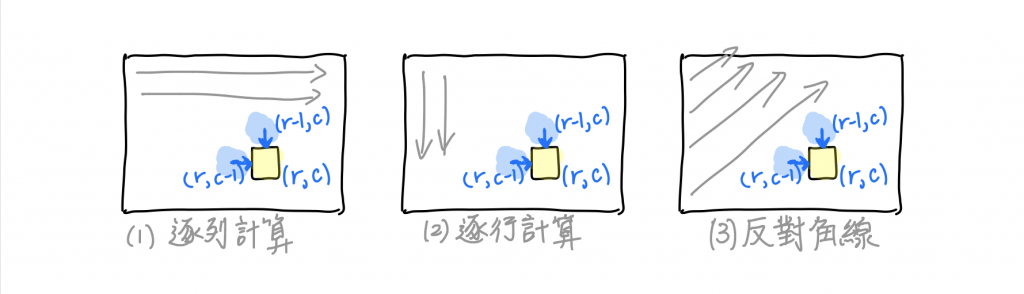
嗯，第三種方法乍看之下沒什麼用（請不要為反對而反對反對角線的計算順序～），但至少算出來也會對啦。備註：用 numpy 的 np.fill([m, n], 1) 初始化表格的可讀性較高，但效能可能較差。（類似題可參考：https://leetcode.com/problems/pascals-triangle-ii/）

接下來我們來同場加映一個只會在程式解題比賽或面試的時候被討論到的東西：迴文字串。我相信迴文字串在實際應用上就跟家用變頻冷氣一樣使用日本製造壓縮機非常非常稀少。什麼是迴文字串呢？就是一個正著讀和反著讀都一樣的字串啦！

Example 4: Leetcode 5 - Longest Palindromic Substring

題目連結

https://leetcode.com/problems/longest-palindromic-substring/

題目敘述

給你一個字串，找出最長的迴文子字串。如果有很多組解的話隨便輸出哪一種都可以。

解題思考

我們可以用 isPalindrome[i, j] 代表從 i~j 位置這段子字串是否是一個迴文。如果它是迴文的話，要嘛 i == j（也就是說只有一個字元）、要嘛 i+1 == j 而且兩個字元相等、要嘛 s[i] == s[j] 而且 isPalindrome[i+1, j-1] 也要是 true。這種時候格子之間的依賴關係就會變得很微妙——計算 (i, j) 這格需要知道 (i+1, j-1) 這格的答案。這時候反對角線就派上用場啦！

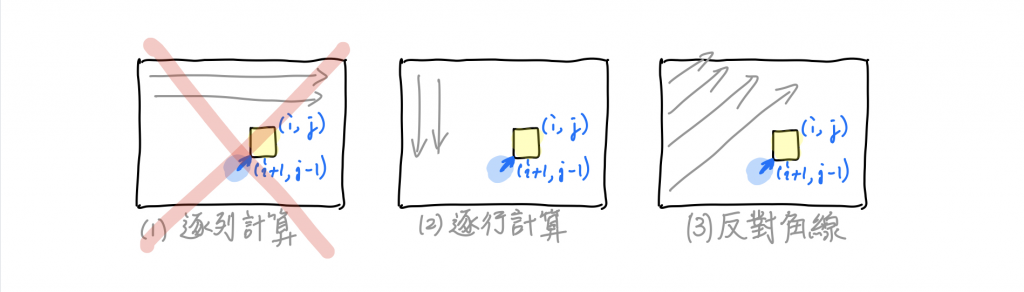
使用逐行計算的參考程式碼：

class Solution:
    def longestPalindrome(self, s: str) -> str:
        n = len(s)
        dp = [[0] * n for _ in range(n)]
        answer = ""
        for j in range(n):
            for i in range(j+1):
                dp[i][j] = (i == j or \
                            (i+1 == j and s[i] == s[j]) or \
                            (i+1 < j and s[i] == s[j] and dp[i+1][j-1] == True))
                if dp[i][j] == True and j-i+1 > len(answer):
                    answer = s[i:j+1]
        return answer

好的～今天看了兩個例子，都是易於填表！看到動態規劃的遞迴式子、看到表格定義基本上程式碼就會溢於言表了～我們明天見！