動態規劃到底可以拿來做什麼呢？根據前兩天我們使用動態規劃解決的問題們，可以歸納出兩種題型：最佳化問題和計數問題。最佳化問題通常要在許多可行解裡面找出一個「最好的答案」，比方說，第一天的找零錢問題，我們的目標就是要找出「使用錢幣最少」的找錢方案。此時「最小化使用的錢幣總數」就是這個最佳化問題的目標函數。

另一方面，計數問題所求的，並非是最好的答案，反而要全面性的計算有幾種可能的答案或其加權總數。比方說昨天的機器人走路問題，就是一個典型的計數問題。絕大多數的計數問題可以使用數學方法來解決。但是，當參數一多的時候，動態規劃的解題觀念就派上用場啦！這可說是用技術來解決計數問題的技術呢呵呵呵

今天我們再來看看兩個計數問題吧～

Example 5: Leetcode 96 - Unique Binary Search Trees

題目連結

https://leetcode.com/problems/unique-binary-search-trees/

題目敘述

如果我們把 1~N 的數字建立出一棵二元搜尋樹，請問總共有幾種樹的長相呢？比方說當 N = 3 的時候，有 5 種不同的二元搜尋樹：

解題思考

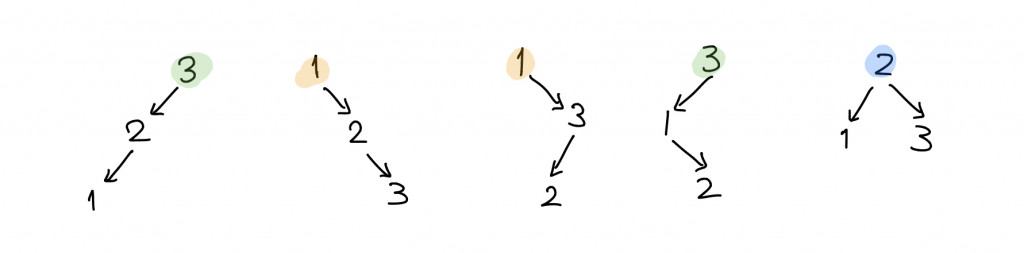
我們可以根據分而治之法 (Divide and Conquer) 來找出計數用的遞迴關係～首先，我們可以觀察到，一棵二元搜尋樹總是要有根的吧！所以取決於這個樹根的值 r，依據定義所有比 r 小的數字都要放在左子樹裡面、而所有比 r 大的數字都要放在右子樹裡面。

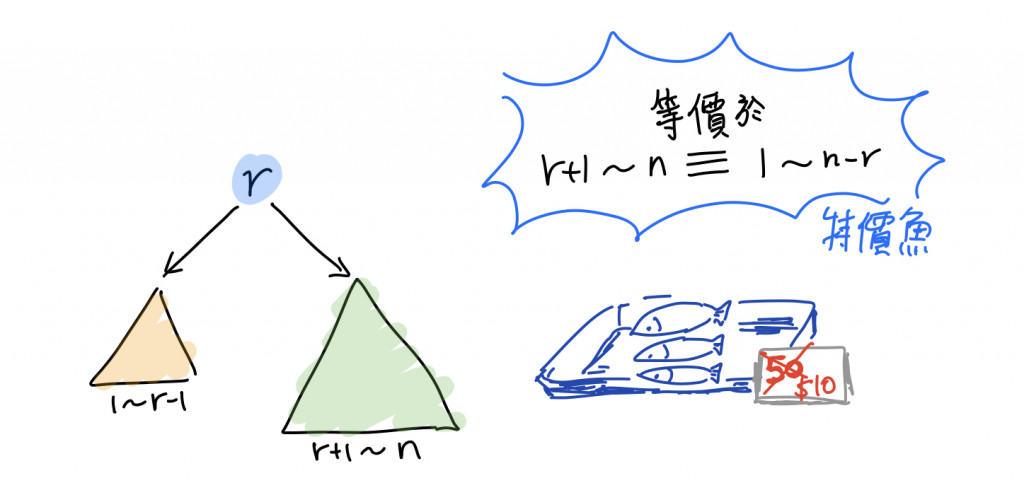
此時左子樹和右子樹的節點數量都比 n 來得小了！而每一種左子樹與右子樹，都會建構出一棵獨一無二的樹，也就是說以 r 為根節點的二元搜尋樹的總數有「左子樹的建構方法數」乘以「右子樹的建構方法數」。動態規劃就在此時默默地跳了進來！於是我們可以根據填表大法，先從 n = 1, 2, … 開始計算，最後找出答案！

參考程式碼(Python3)

class Solution:
    def numTrees(self, n: int) -> int:
        T = {}
        T[0], T[1] = 1, 1
        for k in range(2, n+1):
            T[k] = sum([T[r-1] * T[k-r] for r in range(1, k+1)])
        return T[n]

Example 6: Leetcode 70 - Climbing Stairs

題目連結

https://leetcode.com/problems/climbing-stairs/

題目敘述

現在有 n 階樓梯要爬。每一次你可以跨一階或兩階，請問有幾種爬法呢？

解題思考

假設跨成 n 階的爬法數是 F(n) 種，那麼考慮最後一階是跨一步還是跨兩步：如果是跨一步的話那麼有 F(n-1) 種方法可以踩到第 n-1 階。如果是跨兩步的話就有 F(n-2) 種方法可以踩到第 n-2 階。所以列式子出來會長成 F(n) = F(n-1) + F(n-2) 是不是很眼熟呢？跨零階和一階的方法數都是 1 種，剛好也完整地定義了費氏數列。

參考程式碼(Rust)

因為費氏數列我們第一天寫過了，今天來換換語言換個口味吧～
感覺上 Rust 把 iterator 跟 generator (iter::Scan) 的寫法合併起來了，所以多了這個傳統上 python 得多寫一些東西才有一樣效果的方便寫法。比較精確的說是在建立 stateful iterator 這件事情上給予了很大的方便。這兩天看到覺得很有趣忍不住想跟大家分享！

而且 Rust 跑起來好快啊... 隨隨便便就 0 ms 了。究竟是不是他們測量時間有誤差呢（思）

impl Solution {
    pub fn climb_stairs(n: i32) -> i32 {
        (0..n).scan([0, 1], |state, i| {
            *state = [state[1], state[0] + state[1]];
            Some(state[1])
        }).last().unwrap()
    }
}

有的時候，只要一個小小變化，就可以讓計數問題變成截然不同的最佳化問題。而且這樣的最佳化問題通常更貼近我們想要解決的問題：到底怎樣爬樓梯比較省力(比方說這篇 RunningQuotient 上的文章)？

Example 7: Leetcode 746 - Min Cost Climbing Stairs

題目連結

https://leetcode.com/problems/min-cost-climbing-stairs/

題目敘述

你想要從第 0 階階梯一路爬到第 n 階階梯。但是現在除了第 n 階以外，其餘的 0~n-1 每一階階梯，踩下去以後就要付錢。踩到第 i 階階梯的話要付 cost[i] 元。請問在每一次可以跨一階、或跨兩階的情形下，至少要付多少總額才能夠踩到第 n 階？（請注意：一開始可以從第 0 階或第 1 階開始爬。）

解題思考

跟剛才那題計數問題的想法簡直如出一轍啊！我們只要把原本的定義「踏到第 k 階的方法數」改成「踏到第 k 階的最小花費總額（包含 cost[k]）」就可以了！仔細推敲，能夠踏到第 k 階之前必定踏上第 k-1 階或第 k-2 階。也就是說，踏到第 k 階的最小總花費是前述兩種情形中各自最小總花費的最小值（雖然有點繞口但請習慣它…）再加上 cost[k] 就可以算出我們要的答案啦～

參考程式碼(Python3)

class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        n = len(cost)
        best = {}
        best[0], best[1] = cost[0], cost[1]
        for step in range(2, len(cost)):
            best[step] = min(best[step-1], best[step-2]) + cost[step]
        return min(best[n-2], best[n-1])

好的今天看了兩個計數問題的例子、以及一個最佳化問題的例子，大家對於動態規劃的適用性有沒有覺得好像多理解了什麼呢？沒有的話沒關係，畢竟我們還有27天！再過27天應該就有機會理解自己到底能不能理解動態規劃了！