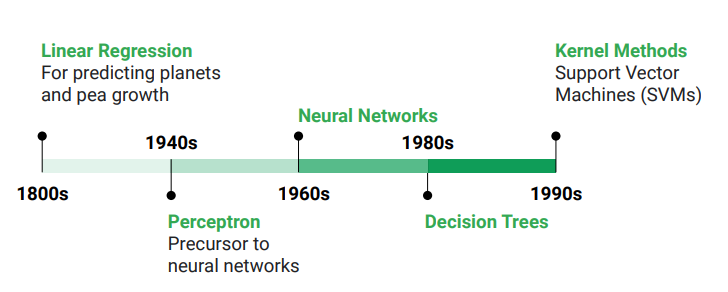
從1990年代開始，核方法領域逐漸形成。 Google研究總監，Corinna Cortes是其中一位先驅。

支持向量機

該研究領域發展出有趣的新非線性模型，最主要的是非線性支持向量機(SVM)，也就是你以前可能聽說過的最大邊距分類器(maximum margin classifiers)。從根本上講，SVM的核心是透過非線性激活函數以及S型輸出，來實現最大邊緣。之前，我們已經看到了如何使用邏輯回歸來創建決策邊界，以最大程度地提高分類概率的最大或然率。

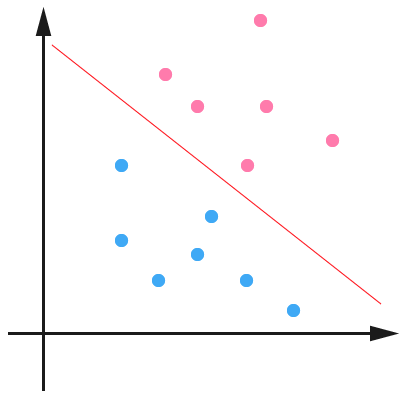
在線性決策邊界的情況下，邏輯回歸希望每個點和相關分類可能遠離超平面，並提供可以解釋為預測區間的機率。你可以在兩個線性可分離的類別之間創建無限數量的超平面，例如兩個超平面，如此處兩個圖中的虛線所示。

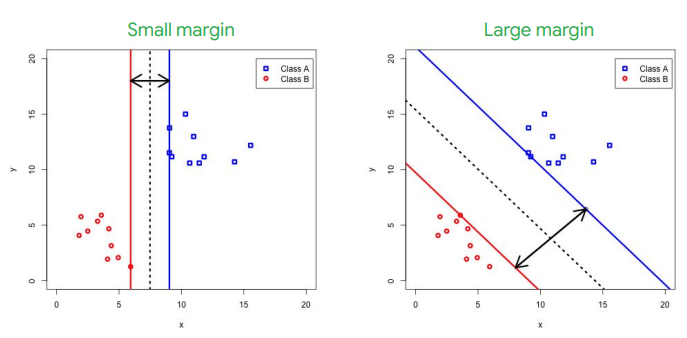
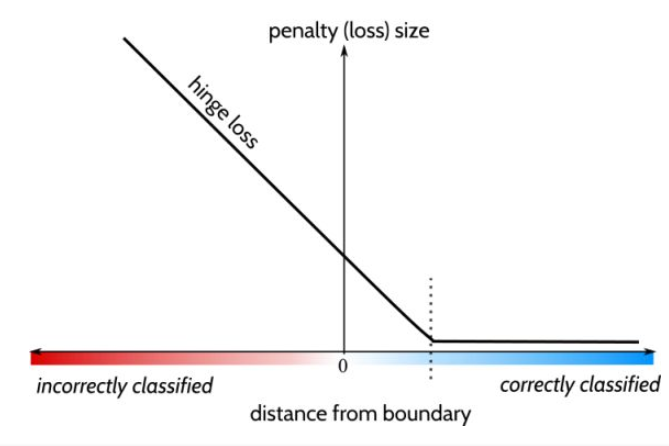
在SVM中，我們在決策邊界超平面的任一側包括兩個平行的超平面，它們與超平面每一側上最接近的數據點相交。這些就是支持向量。兩個單獨的向量之間的距離是邊距(margin)。在左側，我們有一個垂直的超平面，確實將這兩個類別分開。但是，兩個支持向量之間的邊距很小。透過選擇不同的超平面，例如右側的超平面，可以得到更大的邊距。邊距越寬，決策邊界越廣泛，這將使模型對於新數據有更好的表現。因此，與邏輯回歸最小化交叉熵相比，SVM分類器旨在使用鉸鏈損失函數(hinge loss function)來最大化兩個支持向量之間的邊距。

你可能可以注意到，這邊只有兩個分類，這會使它變成一個雙元分類問題。給一個分類的標籤賦予一個值"1"，另一個分類的標籤賦予一個值"-1"。如果有兩個以上的分類，則應採用“一對一”的方法，然後從每個單位的雙元分類中選擇最優解。

核轉換

但是，如果數據不能線性分為兩類，會發生什麼事呢?好消息是，我們可以應用核轉換(kernel transformation)，將數據從輸入向量空間映射到具有可以線性分離功能的向量空間。如圖所示。就像以前一樣，深層神經網絡的興起，大量時間和工作都花在了透過高度調試用戶創造的特徵圖來將原始數據轉換為特徵向量的過程裡。

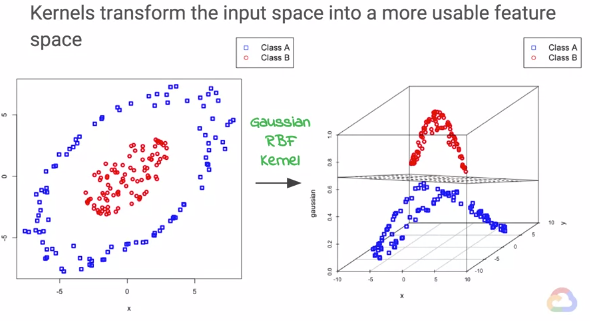
但是，在核方法中，唯一的用戶定義項就是內核，也就是原始數據中表示成對點之間的相似性函數。核變換類似於神經網絡中的激活函數如何將輸入映射到函數以變換空間。每層中神經元的數量能控制維度(dimension)。因此，如果你有兩個輸入且有三個神經元，則會將輸入2D空間映射到3D空間。這邊我們可以看到，核轉換的本質就是將原始數據投射到高維空間中。

核函數

核函數種類繁多，最基本的是基本線性內核、多項式內核(polynomial kernel)和高斯徑向基函數內核(Gaussian radial basis function kernel, RBF)。當我們的雙元分類器使用核函數時，通常會計算相似性的加權和。那麼，什麼時候應該在回歸中使用SVM?核化SVM傾向於提供稀疏(sparse)的答案，因此具有更好的可擴展性(scalability)。當維度很高且預測器幾乎可以肯定預測時，SVM的性能會更好。我們已經看到了SVM如何使用內核將輸入映射到更高維的特徵空間。

而神經網絡中的什麼東西也可以映射到更高維的向量空間?正確的答案是，每層更多的神經元。每層神經元的數量決定了你所在地向量空間的維度數。如果我以三個輸入開始，則我位於R3向量空間中。即使我有一百個層，但每個層只有三個神經元，我仍將處於R3向量空間中，並且只更改基礎。例如，當將高斯RBF內核與SVM一起使用時，輸入空間將映射到無限維。激活函數更改向量空間的基礎，但不增加或減少尺寸。我們可以將它視為簡單的旋轉、拉伸或擠壓。它可能是非線性的，但是你仍然和以前一樣在相同的向量空間中。損失函數是您要盡量減少的目標，它是使用其梯度來更新模型參數權重的純量(scalar)。這只會更改旋轉、拉伸和擠壓的程度，而不會更改尺寸的大小。

延伸閱讀

• 常用的核函數類型

若是覺得本文有幫助，歡迎點選Like、星星收藏或是追蹤系列文支持哦！